Nguy n Đăng Minh Quânễ
L p: 06D5ớ
Nhóm: 8A
Bài t p TRUY N Đ NG ĐI N v gi m t c đ đ ng c m t chi u kích tậ Ề Ộ Ệ ề ả ố ộ ộ ơ ộ ề ừ
đ c l p b ng cách gi m đi n áp ph n ngộ ậ ằ ả ệ ầ ứ
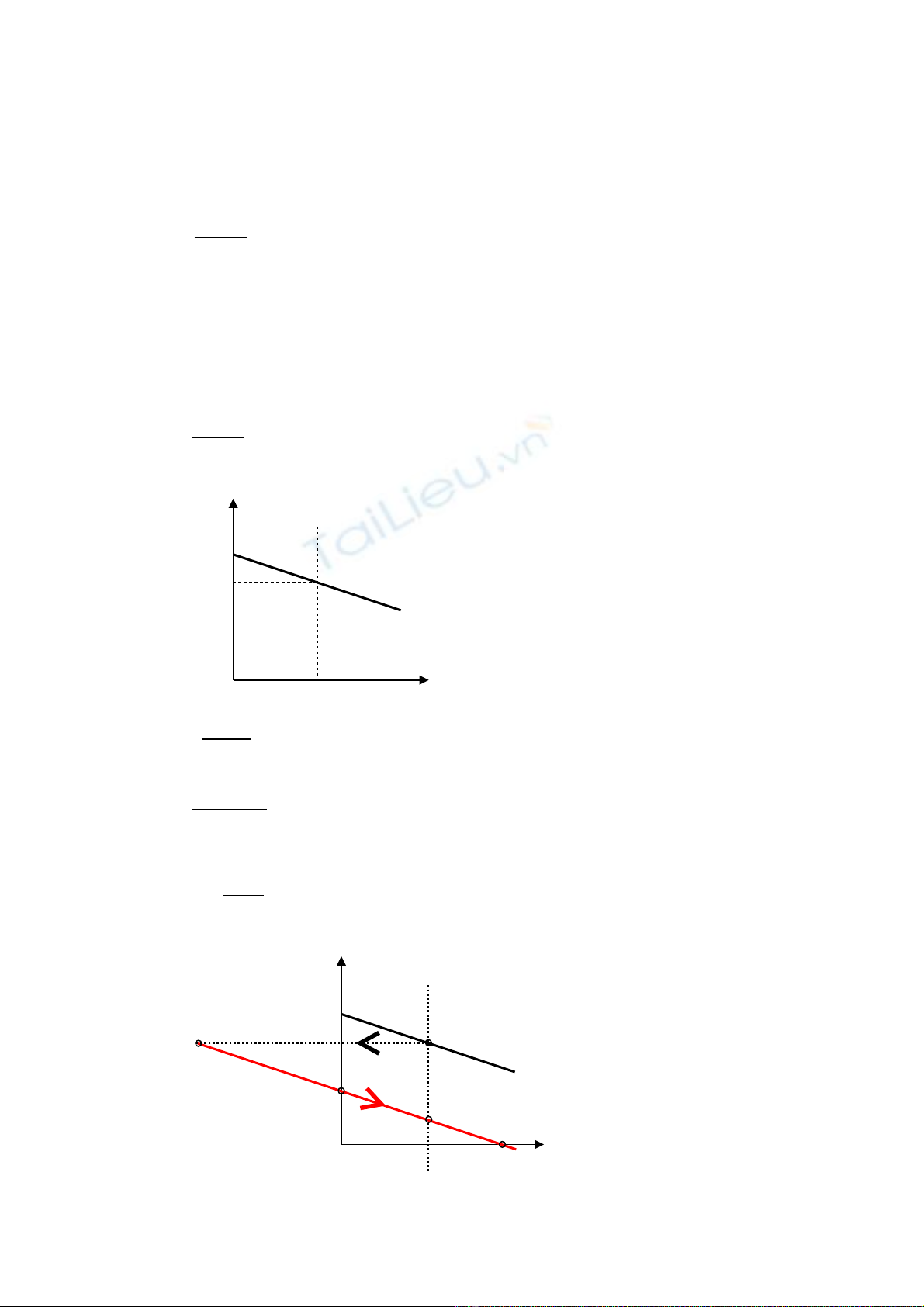
Cho đ ng c kích t đ c l p v i các thông s c b n sau:ộ ơ ừ ộ ậ ớ ố ơ ả
Pđm; U đmư; I đmư; Uktđm; Iktđm; Rư; Rkt; Lư; Lkt; nđm; p;a
Gi thi t đ ng c làm vi c ch đ đ nh m c v i mômen c n không đ i Mả ế ộ ơ ệ ở ế ộ ị ứ ớ ả ổ C
= Mđm .
V i các thông s trên ta có th tính đ c các thông s sau:ớ ố ể ượ ố
dm
dm
dm
dm
dm
2 n [rad/s]
60
P
M [Nm]
π
ω =
=ω
Eđmư = U đmư – RưIđmư
pN
K2 a
=π
udm
dm
dm
E
K.
φ = ω
Ta có đ c tính c c a đ ng c :ặ ơ ủ ộ ơ
( )
udm
0TN
dm
2
dm
TN
u
U
K.
K.
R
ω = φ
φ
β =
Gi m t c đ đ ng c b ng cách gi m đi n áp ph n ng Uả ố ộ ộ ơ ằ ả ệ ầ ứ ư .
Đ t: ặ
u
u udm
udm
U
x U x.U
U
= ⇒ =
v i x < 1ớ
Lúc này đ ng c s chuy n v đi m làm vi c m iộ ơ ẽ ể ề ể ệ ớ
oTN
ω
dm
ω
C dm
M M
=
ω
M
oTN
ω
dm
ω
oTN
ω
oNT
ω
ω
M
C
M
nmNT
M
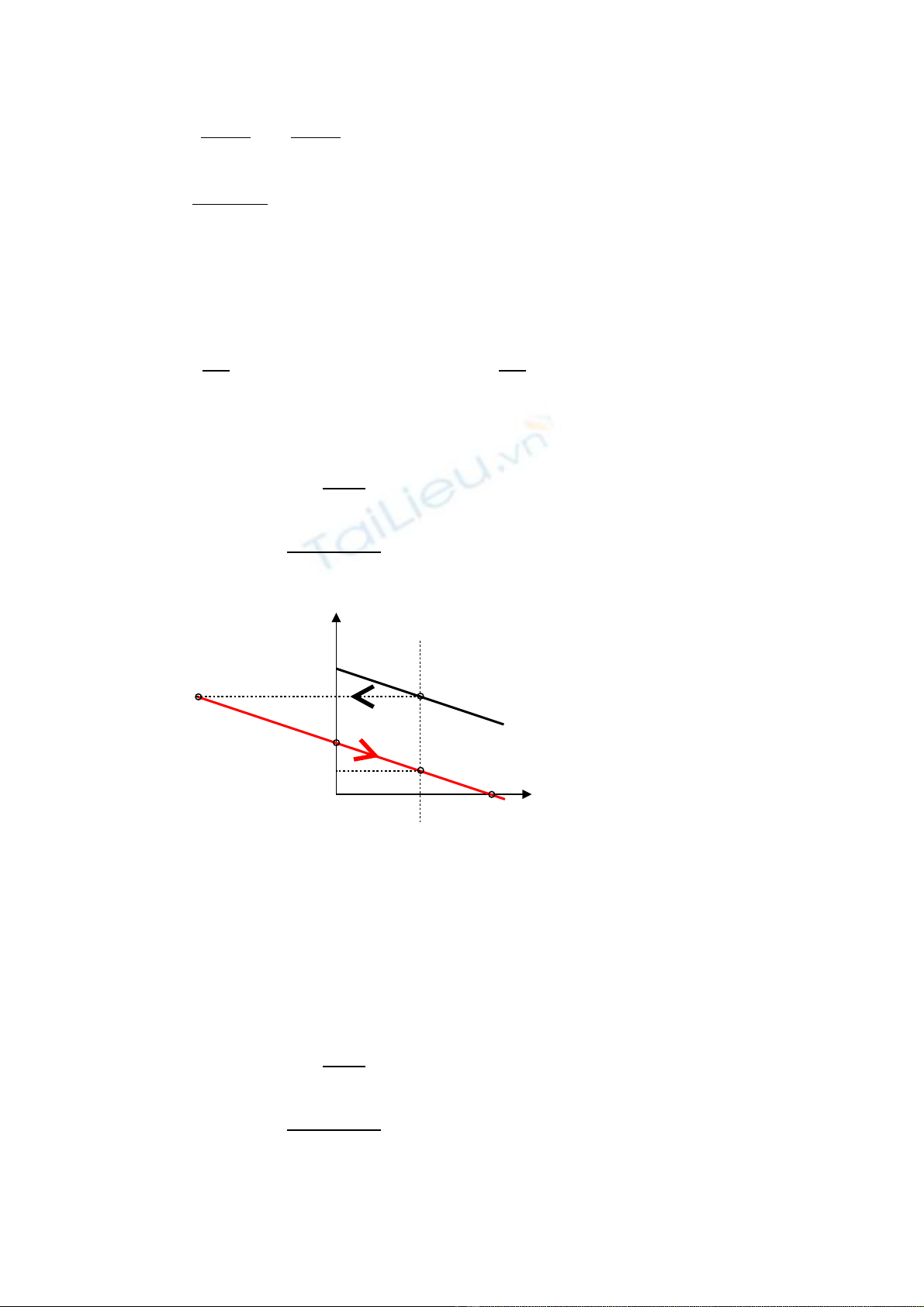
Khi gi m đi n áp ph n ng ta có:ả ệ ầ ứ
u udm
oNT oTN
dm dm
U U
x. x.
K. K.
ω = = = ω
φ φ
( )
2
dm
NT T N
u
K.
R
φ
β = = β
Nh v y trong kho ng th i gian gi m t c đ t t c đ đinh m c ư ậ ả ờ ả ố ộ ừ ố ộ ứ ωđm v t cề ố
đ không t i nhân t o ộ ả ạ ωoNT thì đ ng c ho t đ ng ch đ hãm tái sinh.ộ ơ ạ ộ ở ế ộ
Khi ω = 0
Tr ng h p: Mườ ợ nmNT > MC
nmNT C dm
u dm
dm dm
u
dm u
u dm dm
M M M
U
x.K. . M
R
M .R
xU .K.
⇔ > =
⇔ φ >
⇔ > φ
Trong tr ng h p này đi m làm vi c xác l p m i c a đ ng c có ườ ợ ể ệ ậ ớ ủ ộ ơ ω1 > 0. V yậ
trong kho ng th i gian đ ng c gi m t c đ t t c đ không t i nhân t oả ờ ộ ơ ả ố ộ ừ ố ộ ả ạ
ωoNT v t c đ xác l p m i ề ố ộ ậ ớ ω1 thì đ ng c ho t đ ng bình th ng, chi uộ ơ ạ ộ ườ ề
quay không thay đ i.ổ
Tr ng h p: Mườ ợ nmNT ≤ MC
nmNT C dm
u dm
dm dm
u
dm u
u dm dm
M M M
U
x.K. . M
R
M .R
xU .K.
⇔ ≥ =
⇔ φ ≤
⇔ ≤ φ
oTN
ω
dm
ω
oTN
ω
oNT
ω
ω
M
C
M
nmNT
M
1
ω
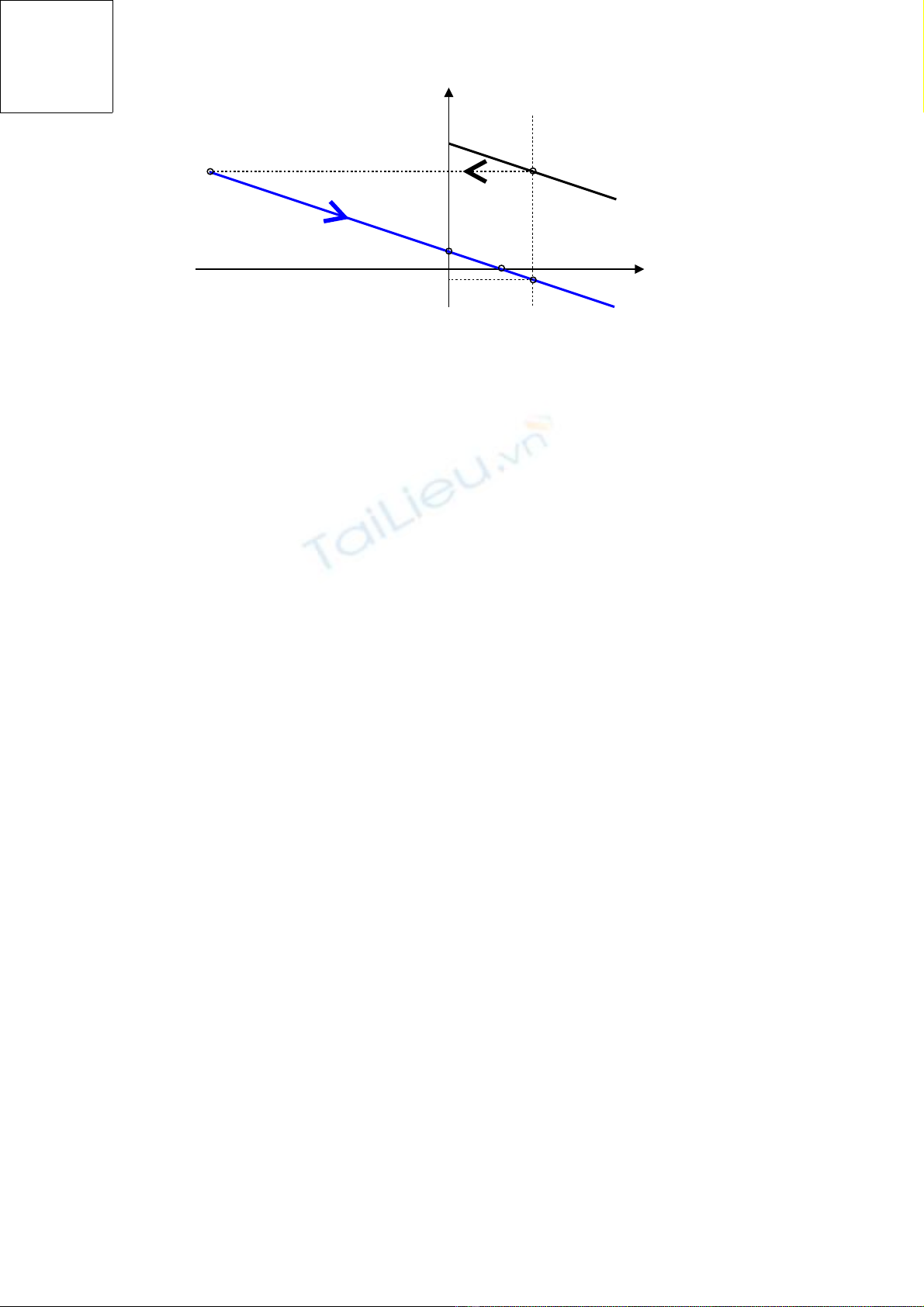
Trong tr ng h p này đi m làm vi c xác l p m i c a đ ng c có ườ ợ ể ệ ậ ớ ủ ộ ơ ω2 < 0.
V y trong kho ng th i gian đ ng c gi m t c đ t t c đ không t i nhânậ ả ờ ộ ơ ả ố ộ ừ ố ộ ả
t o ạωoNT v t c đ ề ố ộ ω = 0 thì đ ng c ho t đ ng bình th ng chi u quayộ ơ ạ ộ ườ ề
không thay đ i; và trong th i gian đ ng c gi m t c đ t t c đ ổ ờ ộ ơ ả ố ộ ừ ố ộ ω = 0 về
v t c đ xác l p m i ề ố ộ ậ ớ ω2 thì đ ng c ho t đ ng ch đ hãm ng c đo đóộ ơ ạ ộ ở ế ộ ượ
đ ng c quay ng cộ ơ ượ
oTN
ω
dm
ω
oTN
ω
oNT
ω
ω
M
C
M
nmNT
M
2
ω