Báo cáo khoa học:
Mô hình hoá kinh tế nông hộ ở miền Bắc:
Mô hình cân bằng cung cầu trong hộ
T¹pchÝKHKTN«ngnghiÖp2007:TËpV,Sè2:8795
§¹ihäcN«ngnghiÖpI


ModelingfarmhouseholdsintheNorth:thehouseholdsupplyanddemandmodel
Ph¹mV¨nHïng1
SUMMARY


          
             



             
!


"#$
1.§ÆTVÊN§Ò
*
TõkhicãNghÞquyÕt10cñaBéChÝnhtrÞ
(1988),hén«ngd©n®−îccoil(®¬nvÞkinhtÕ
tù chñ. C¸cnguån lùc s¶n xuÊt cña hé ®−îc
gi¶iphãng,s¶nxuÊtn«ngnghiÖpcãb−íctiÕn
v−îtbËctrong2thËpkûgÇn®©y.§Õnnay,hé
n«ngd©nv(kinhtÕhén«ngd©nvÉn®ãngvai
trßquanträng®èivíiquècgia.TheokÕtqu¶
tæng hîp s¬ bé cña cuéc Tæng ®iÒu tra n«ng
th«n,n«ngnghiÖpv(thñys¶n,®Õn01/7/2006,
c¶n−íccã10,46triÖuhén«ng,l©mnghiÖpv(
thñys¶n(trong®ãkhuvùcn«ngth«nl(9,78
triÖu hé). Tuy nhiªn, trong sè n(y chØ cã
67,9% sè hé cã nguån thu nhËp lín nhÊt tõ
ho¹t®éngs¶nxuÊtn«ng,l©mnghiÖpv(thñy
s¶n (Ban chØ ®¹o Trung −¬ng Tæng ®iÒu tra
n«ng th«n, n«ng nghiÖp v( thñy s¶n, 2006).
§iÒu®ãchothÊyc¬cÊung(nhnghÒcñahécã
chuyÓnbiÕntrongnh÷ngn¨mquanh−ngcßn
chËm.VËy®èivíin«nghé,t(inguyªnn(ol(

1
KhoaKinhtÕ&PTNT,§¹ihäcN«ngnghiÖpI.
t(inguyªnkhanhiÕmnhÊtv(r(ngbuécn(ol(
nh÷ng r(ng buéc lín nhÊt c¶n trë kh¶ n¨ng
ph¸ttriÓncñahé.NÕuchóngtacãthÓt×mra
nh÷ngc¶ntrën(yth×cãthÓcã nh÷ngchÝnh
s¸chthÝchhîpthøc®ÈykinhtÕhénãiriªngv(
kinh tÕ n«ng th«n nãi chung ph¸t triÓn. Mét
trongnh÷ngh−íngnghiªncøuth−êng®−îc¸p
dông hiÖu qu¶ nhÊt l( sö dông ph−¬ng ph¸p
m«h×nhhãanh»mm«phángsùthay®æic¸c
®iÒukiÖn(kÞchb¶n)®Ót×mranh÷ngh¹nchÕ
®èivíikinhtÕhé(Mooreetal.,1993).
Môctiªucñab(in(yl(x©ydùngv(®Ò
xuÊtmétm«h×nhph©ntÝchkinhtÕhé,trong
®ã cã kÕt hîp ®ång thêi c¸c ý t−ëng vÒ m«
h×nh c©n b»ng kh«ng gian v( m« h×nh c©n
b»ng c¸c ng(nh (ho¹t ®éng s¶n xuÊt) trong
hé.Trªnc¬sëm«h×nhx©ydùng,m«pháng
sùthay®æimétsè®iÒukiÖnnh»mt×mrat¸c
®éng cña viÖc thay ®æi c¸c chÝnh s¸ch. CÊu
tróc cña b(i gåm nh÷ng néi dung sau: PhÇn
tiÕp theo cña b(i tr×nh b(y vÒ ý t−ëng x©y
dùng m« h×nh lý thuyÕt. M« h×nh thùc
nghiÖm ®−îc tr×nh b(y trong phÇn thø 3.

PhÇn 4 sÏ m« t¶ sè liÖu v( c¸c ®Çu v(o cña
m« h×nh. PhÇn 5 l( kÕt qu¶ −íc l−îng, m«
pháng v( th¶o luËn vÒ nh÷ng kÕt qu¶ n(y.
Nh÷ng kÕt luËn v( ®Ò xuÊt ®−îc tr×nh b(y
trongnéidungcuèicñab(i.
2.M¤H×NHLýTHUYÕT
TheoFrankEllis(1998)hén«ngd©ncã
®Æc®iÓm®ångthêivõal( ng−êis¶nxuÊtv(
ng−êi tiªu dïng s¶n phÈm m( m×nh s¶n xuÊt
ra.§iÒun(ydÔd(ngnhËnranhÊtl(khis¶n
xuÊtn«ngnghiÖpcßntùcung,tùcÊpl(chÝnh.
Do ®ã, m« h×nh hãa cÇn ph¶i kÕt hîp ®ång
thêi lý thuyÕt ng−êi s¶n xuÊt v( lý thuyÕt
ng−êitiªudïng.
Hén«ngd©ns¶nxuÊtv(ho¹t®éngn»m
trong mèi t−¬ng quan r(ng buéc víi c¸c hé
kh¸ctrongph¹mvimétl(ng.VÝdô®Êt®ail(
métnguånlùcchÝnhcñac¸chév(n«ngd©n
®−îcgiaoquyÒnchuyÓnnh−îng,chothuªhay
chothuªl¹i®Êt®ai.Tuynhiªn,nh÷ngquyÒn
n(y hÇu hÕt ®Òu thùc hiÖn trong ph¹m vi
l(ng/xãm. Lao ®éng n«ng th«n ng(y c(ng
kiÕm ®−îc nhiÒu viÖc l(m ë c¸c th(nh phè,
nh−ngngaytrongph¹mvimétl(ngth×còng
xuÊthiÖnmétsèhéchothuªlao®éng,métsè
kh¸c®ithuªv(métsèhéth×tùcung,tùcÊp
vÒ lao ®éng1.C¸cnguån lùc s¶n xuÊt cã thÓ
®−îc chuyÓn tõ hé n(y sang hé kh¸c v( nh−
vËynguånlùcsÏ®−îcchuyÓnchonh÷nghé
södôngcãhiÖuqu¶h¬n.
M« h×nh c©n b»ng kh«ng gian ®−îc x©y
dùngdùatrªnkh¸iniÖmvÒtrao®æih(nghãa
gi÷ac¸cvïngv(tõngvïng®Òucãc¶cungv(
cÇuh(nghãa.§èivíitr−ênghîptrao®æi®Êt
gi÷ac¸chéth×mçihésÏcãcung®Êt®aid−íi
d¹ng mét sè thöa ®Êt (hoÆc diÖn tÝch ®Êt) v(
cÇuvÒ®Êt®ai®ãdùatrªnviÖcsödông®Êt®ai
chos¶nxuÊtcñahé.Gi¶sötrongl(ngcãm
hé,mçihéchØcãdiÖntÝchl(ai,khi®ãcung
v(cÇu®Êt®aitrongl(ngcãthÓ®−îcbiÓudiÔn
nh−sau(Hïngv(céngsù,2006):
Ax=

a
1
a
1
a
1
a
2
a
2
a
2
a
m
a
m
a
m
(mxm2)
Ay=
m
m
m
aaa
aaa
aaa
21
21
21
ΟΟΟ
Λ
(mxm2)
Trong ®ã: ma trËn Ax v( Ay ph¶n ¸nh
cungv(cÇu®Êt®ai2.
S¶nphÈms¶nxuÊtracñahécòngcãthÓ
®−îctrao ®æivíic¸chékh¸ctrongph¹mvi
l(ng hay víi c¸c l(ng kh¸c. Sù trao ®æi phô
thuécv(omøc®éthÆngd−cungv(cÇu(®−îc
ph¶n ¸nh bëi riªngtõng hé). Dßng h(ng hãa
n(ysÏx¸c®Þnhb¶nchÊtcñatrao®æi.DovËy,
m« h×nh hãa kinh tÕ hé cÇn xÐt ®Õn yÕu tè
kh«nggian.Ngo(ira,hécßnsödôngnh÷ng
s¶n phÈm n(y cho tiªu dïng néi bé cña gia
®×nhnh−®Ó¨nv(ch¨nnu«i.DovËy,m«h×nh
hãakinhtÕhécòngnªnkÕthîp®ångthêic¶
m« h×nh c©n b»ng cung cÇu trong hé v( m«
h×nhc©nb»ngkh«nggian.
D−íid¹ngto¸nhäc,m«h×nhcãthÓbiÓu
diÔnnh−sau:
1
Méttrongnh÷ng®Æctr−ngcñalao®éngl(kh«ngdùtr÷®−îc.
2
NÕumçihécãnthöa®Êtth×matrËnA
x
v(A
y
sÏcãbËcmx(m
2
xn).
M«h×nhho¸kinhtÕn«nghéëmiÒnB¾c...
MaxZ=
' '
1 1= =
−
∑ ∑
n n
j j jx j
j j
P Q P X
(1)
Víir(ngbuéc
Ax
≤
ax
Ay
≤
ay
Qj=f(ay,Xj)
Pjxdpjq
≤
0
Q,D≥0.
Trong ®ã: Z l( tæng lîi nhuËn/thu nhËp
cñahé(hoÆccñatÊtc¶c¸chétrongl(ng);
Pl(vÐct¬cñagi¸s¶nphÈm;
Ql(vÐct¬cñas¶nl−îngcñahé(c¸ché);
Pxl(vÐct¬cñagi¸c¸c®Çuv(o;
Xl(vÐct¬cñal−îngc¸c®Çuv(osödông
cñahé(hoÆctÊtc¶c¸ché);
axl(tængcung®Êt®aicñatõnghé;
ayl(tængcÇu®Êt®aicñatõnghé;
Axv(Ayl(2matrËncãbËcmxm2ph¶n
¸nhdiÖntÝchcñatõnghé.
S¶nl−îng(Qj)cãthÓl(h(msècñadiÖn
tÝch®Êt®ai,ay v(c¸c®Çuv(okh¸c.Gi¶thiÕt
r»ngmçihén«ngd©ncãdiÖntÝchl(ai v(cã
m hé. Thöa ®Êt víi diÖn tÝch ai cã thÓ ®−îc
cungchohéihoÆcl(méthén(o®ã.
M« h×nh (1) cùc ®¹i tæng lîi nhuËn/thu
nhËp cña tÊt c¶ c¸c hé trong ph¹m vi l(ng
hoÆcvïngvíir(ngbuécl(:Cungv(cÇu®Êt
®ai, h(m s¶n xuÊt cña s¶n xuÊt n«ng nghiÖp
(bao gåm c¶ trång trät v( ch¨n nu«i), lîi
nhuËnkh«ng©mchotõnghév(®¸pøngthu
nhËptèithiÓuchotõnghén«ngd©n.Ngo(ira,
m« h×nh trªn còng cã thÓ më réng ®Ó ®−a
thªmc¸cho¹t®éngkh¸cnh−chiphÝgiaodÞch
cñathÞtr−êng®Êt®ai,c¸cho¹t®éngtÝndông
cñahé;s¶nxuÊth(nghãaZ(h(nghãakh«ng
rathÞtr−êng).
3.X¢YDùNGM¤H×NHTHùCNGHIÖM
3.1.Gi¶thiÕtcñam«h×nh
Bëim«h×nhthùcnghiÖm®−îcx©ydùng
v(gi¶itheolýthuyÕtcñab(ito¸nquyho¹ch,
do®ãrÊtnhiÒuth«ngtincÇnph¶icãvÒmèi
quanhÖsèl−îngv(c¶gi¸trÞgi÷ac¸cho¹t
®éngs¶nxuÊtv(nguånlùcchos¶nxuÊt.Nãi
c¸chkh¸c,nã®ßiháinh÷ngkiÕnthøcvÒkü
thuËt®èivíic¸cc«ngthøclu©ncanhv(c¸c
yªu cÇu vÒ ®Çu v(o cho s¶n xuÊt n«ng
nghiÖp. C¸c hÖ sè trong m« h×nh quy ho¹ch
l(®Æcthïv(møc®échÝnhx¸ct−¬ng®èicña
c¸c hÖ sè n(y sÏ cã ¶nh h−ëng lín ®Õn kÕt
qu¶cñam«h×nh.
M« h×nh hãa c¸c kh¶ n¨ng x¶y ra trong
giao dÞch ®Êt th× h(ng lo¹t vÊn ®Ò cÇn ph¶i
xemxÐtv(®−îc®−av(om«h×nh.CôthÓgiao
dÞch ®Êt gi÷a c¸ché ®ßi hái cÇn ph¶i cã thÞ
tr−êng®Êt®aiho¹t®éng,trongtr−ênghîpcña
ViÖt Nam l( chuyÓn nh−îng quyÒn sö dông
®Êt.X©ydùngm«h×nh®Ó®¸nhgi¸trªnph¹m
viréngth×c¸cthamsèliªnquan®Õntrao®æi
®Êt®aith×cÇnph¶icãgi¶thiÕtthÞtr−êng®Êt
®aitånt¹iv(chóngta®ybiÕttr−ícc¸cchiphÝ
giaodÞch.X©ydùngm«h×nhgiaodÞch®Êtë
cÊpn«nghév(cÊpl(ng,xycòngcÇnph¶icã
gi¶ thiÕt l( thÞ tr−êng lao ®éng tån t¹i, ë ®ã
n«ngd©ncãthÓ®ithuªthªmlao®éngchoc¸c
ho¹t®éngn«ngnghiÖpcñam×nhhoÆccãthÓ
kiÕm ®−îc viÖc l(m phi n«ng nghiÖp. Ngo(i
ra,vènchos¶nxuÊttrångträtcòngcãthÓ®i
vayhaychuyÓntõb¸nc¸cs¶nphÈms¶nxuÊt
rav(tõchothuª®Êt.
3.2.CÊutróccñam«h×nh
ThunhËpcñahégi¶thiÕtl(tõ3nguånc¬
b¶n: Trång trät, ch¨n nu«i v( ®i l(m thuª.
Môc tiªu cña m« h×nh l( cùc ®¹i tæng lîi
nhuËn hay thu nhËp cña c¸c hé trong l(ng,
trong ®ã tæng lîi nhuËn/thu nhËp ®−îc x¸c
®Þnhl(gi¸trÞb¸nc¸cs¶nphÈmtrångträttrõ
®i tæng c¸c chi phÝ biÕn ®æi. §èi víi ng(nh
trångträt,c¸cchiphÝn(ybaogåmc¸cchiphÝ
cho ®Çu v(o ®y sö dông, ®i thuª ®Êt, chi phÝ
giaodÞchtrongthÞtr−êngthuªm−ín®Êt®ai,
thuÕv(c¸ckho¶nphÝv(c¸cchiphÝsödông
bëic¸ché.ChiphÝchoch¨nnu«igåmchiphÝ
gièng, thøc ¨n, lao ®éng v( c¸c kho¶n chi
kh¸c.R(ngbuécchÝnhtrongm«h×nh®èivíi
sö dông ®Êt sÏ bao gåm cung v( cÇu ®Êt ®ai
cñatõnghétrongtængsèmhé,diÖntÝchgieo
trångcñac¸cc©ytrångtõnghécãkh¶n¨ng
chotõngvô.§Óph¶n¸nht×nhh×nhs¶nxuÊttù
cung,tùcÊpv(h¹nmøccho®Êtlóa,s¶nxuÊt
lóa cña tõng hé ph¶i ®¸p øng nhu cÇu tiªu

dïng tèi thiÓu cña hé. PhÇn cßn l¹i cña s¶n
l−îng lóahé cãthÓ ®em b¸n hoÆc dïng cho
ch¨nnu«i.Nh−vËy,lóa®−îcs¶nxuÊtcho2
môc®Ýchl(tiªudïngnéibétronghév(®em
b¸nrathÞtr−êng.Gi¶thiÕtr»nghékh«ngdù
tr÷ lóa g¹o v( c¸c s¶n phÈm kh¸c. C©n b»ng
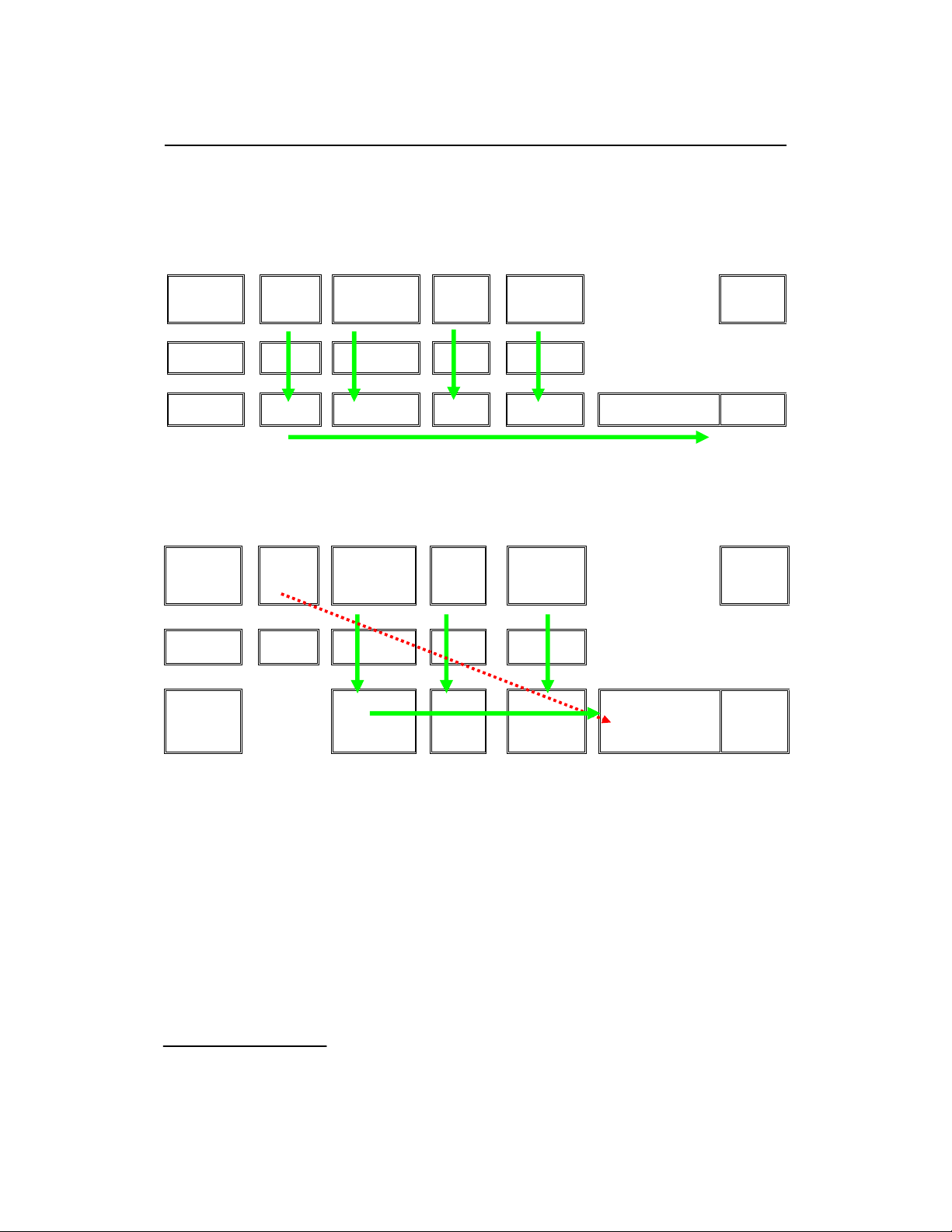
s¶nphÈmtronghécãthÓ®−îcm«phángnh−
h×nhd−íi®©y:
Tr−ênghîpc©nb»ng1: 
X
j
DTlóa
L−îng
thãcb¸n
Tiªu
dïng
Thãc®Ó
ch¨nnu«i
RHS
C
j
0
+Gi¸
0
0
C©nb»ng1
NS
1
1
1
Sumproduct(...) ≤0
Trongc©nb»ngn(y: S¶nl−îng≥tiªudïng+b¸n+södôngchoch¨nnu«i
Hay NSxDT≥tiªudïng+b¸n+södôngchoch¨nnu«i
Tr−ênghîpc©nb»ng2: 
X
j
DTlóa
L−îng
thãcb¸n
Tiªu
dïng
Thãc®Óch¨n
nu«i
RHS
C
j
0
+Gi¸
0 0
C©nb»ng2
1
1
1
Sumproduct(...)
f(DTgieo
trång,D)
≤0
Trongc©nb»ngn(y:
L−îng tiªu dïng + b¸n + sö dông cho
ch¨nnu«i≤f(DTgieotrång,D).
Trong®ã:fl(d¹ngh(ms¶nxuÊt,NSl(
n¨ng suÊt c©y trång, DT l( diÖn tÝch, D l(
vect¬c¸c®Çuv(obiÕn®æi®−îc®−av(om«
h×nhhãa3.
Trong s¬ ®å trªn, mòi tªn liÒn (nÐt liÒn)
ph¶n¸nhmèiquanhÖtrùctiÕptheo2tr−êng
hîp c©n b»ng. Trong m« h×nh 1, cung s¶n
phÈmbiÓuhiÖnëNS(dÊu©m)v(kh«ng®æi
trong khi cÇu s¶n phÈm bao gåm l−îng b¸n,
l−îng tiªu dïng v( l−îng cho ch¨n nu«i.
Trongc©nb»ng2,mét®iÓmkh¸cbiÖtl(cung
s¶nphÈm®−îcph¶n¸nhtrongh(ms¶nxuÊtf
(DT gieo trång, D) hay nãi c¸ch kh¸c s¶n
l−îngcñahétrongtr−ênghîpn(yphôthuéc
v(oc¸cbiÕncñam«h×nh.NÕuh(mfl(h(m
phituyÕnth×m«h×nh−ícl−îng(1)sÏl(m«
h×nhphituyÕn.
Ngo(i lóa, c¸c c©y trång kh¸c s¶n xuÊt
chñyÕu®Ób¸nrathÞtr−êngv(cãthÓphôcvô
ch¨nnu«i(ng«,®Ëut−¬ng).TængchÝphÝs¶n
xuÊttrångträttõng vôcñahébaogåmtæng
chiphÝbiÕn®æicñatÊtc¶c¸cc©ytrångtrong
3
Nh÷ngbiÕnkh«ng®−av(om«h×nhm(cãtrongh(mfcãthÓsödôngëmøcb×nhqu©n.