BÁO CÁO THÍ NGHIỆM BÀI 3
ĐO HỆ SỐ HALL
Nhóm 5: 1. Lê Văn Thuận
2. Nguyễn Thị Thúy Tình
3. Trần Thị Tuyết
4. Thongphanh Xiayalee
Lớp: Cao học Vật lí K22.
Chuyên ngành: Lý luận và Phương pháp giảng dạy Vật lí.
Ngày thực hành: 24/5/2013.
I. Tóm tắt nội dung
Giả sử ta có một mẫu phẳng bán dẫn có chiều dày d, có bốn tiếp điểm
A, B, C, D. Cho dòng điện chạy vào bán dẫn qua tiếp điểm A, C ( IAC). Do sự
chênh lệch điện áp giữa B và D ngay cả khi từ trường bằng 0. UBD khi đó
được xác định như sau:
Thay đổi giá trị của dòng điện và ghi lại những giá trị tương ứng của
hiệu điện thế UBD, đây là hiệu điện thế giữa hai điểm B, D khi từ trường bằng
0.
Cho dòng điện chạy vào nam châm điện. Dưới tác dụng của từ trường
cuộn dây thi electron và lỗ trống cùng chạy về một mặt của bán dẫn, do đó sẽ
xuất hiện một hiệu điện thế UBD mới.Do giá trị của nó trong các trường hợp
sau:
+ Cho B một giá trị không đổi trong giới hạn cho phép (Bmax =0,6 T),
thay đổi I ( bằng cách điều chỉnh biến trở), ghi lại các giá trị của UBD tương
ứng.
+ Cho IAC một giá trị xác định trong giới han IMax=30mA, thay đổi B
(bằng cách thay đổi dòng vào nam châm điện) và ghi lại những giá trị của UBD
hiển thị trên vôn kế.
II. Kết quả thí nghiệm
a) Điều kiện thực hiện phép đo.
- Phép đo được thực hiện nhờ 1 nam châm điện có thể tạo ra từ
trường cực đại Bmax = 0.6T.
- Mẫu đo là một lá đồng hình chữ nhật có bề dày d = 0.5mm đặt
vuông góc với từ trường của nam châm điện.
- Hiệu điện thế UBD được đo nhờ một vôn kế điện tử.
b) Kết quả.
- Xử lý bằng số liệu.
Vậy
1.952 0.033
H
R (10-5 Ω/T)
- Xử lý bằng đồ thị.
Ta có: ( 0) ( 0)
( )
. .
H CD B CD B
AC
d d
R U U U
I B B I
.H
d
I U
B R
Bảng số liệu:
IAC(mA)
10 20 30 40 50 60
∆U(mV)
0.120 0.235 0.348 0.465 0.57 0.688
Sử dụng phần mền Origin ta thu được hàm của IAC theo ∆UBD
I(mA) U(mV) RH
(10-5 Ω/T)
H
(10-5 Ω/T)
B = 0(T) B = 0.3(T)
10 0.131 0.010 2.017 0.065
20 0.257 0.021 1.967 0.015
30 0.387 0.033 1.967 0.015
40 0.509 0.042 1.946 0.012
50 0.627 0.050 1.903 0.049
60 0.749 0.061 1.911 0.041
Giá trị
trung bình
1.952 0.033
Chiều dài mẫu : d = 0.5mm
( 0) ( 0)
( )
.
H CD B CD B
AC
d
R U U
I B
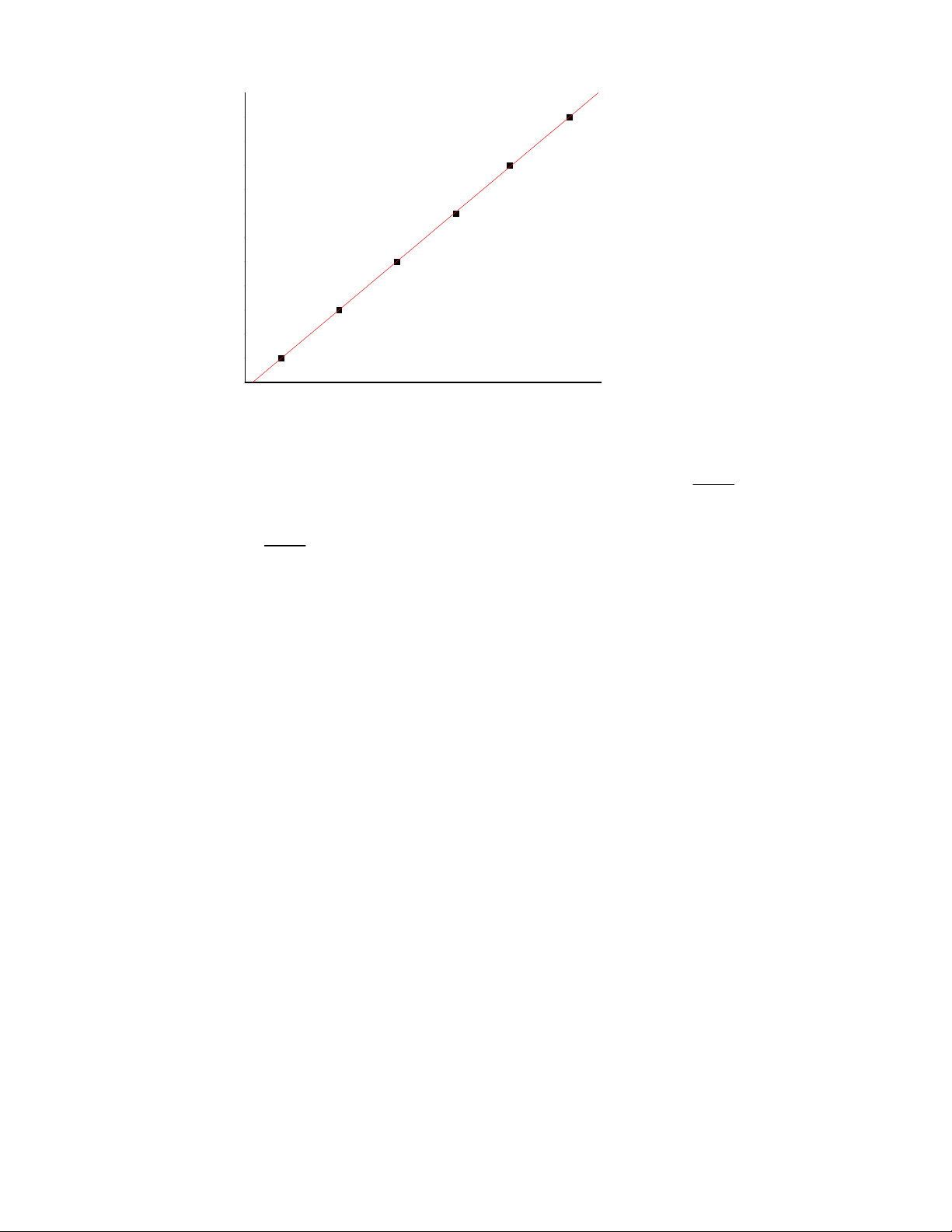
0.1 0.2 0.3 0.4 0.5 0.6 0.7
10
20
30
40
50
60
Y =-0.73693+88.38489 X
I ( mA)
UCD(B=0)-UCD(B=0.3)
Hệ số góc của đường thẳng ta thu được chính là giá trị của
.
H
d
B R
.
H
d
B R
= 88.38589 với 0.5
0.3
d mm
B T
RH = 1.885691 (10-5 Ω/T)
c) Các yếu tố ảnh hưởng đến phép đo.
- Khách quan:
+ Điện trở các điểm nối trong mạch không thể bỏ qua.
+ Từ trường đi qua mẫu có thể bị ảnh hưởng bởi từ trường trái đất và
từ trường do các thiết bị xung quanh gây ra.
+ Mẫu có thể không được đặt vuông góc với từ trường của nam châm
điện.
- Chủ quan:
+ Thao tác thay đổi cường độ IAC còn chưa chuẩn xác.
III. Thảo luận kết quả
Theo như lý thuyết chúng ta xây dựng thì hệ số Hall phụ thuộc vào
nồng độ hạt tải( electron và lỗ trống) khi cho dòng điện chạy qua bán dẫn và
đặt bán dẫn này trong từ trường thì trong bán dẫn nồng độ hạt tải không
ngừng thay đổi (do no luôn luôn xảy ra quá trình bứt các e và quá trình tái hợp
giữa e và lỗ trống), trong mỗi một điều kiện nhất định của từ trường cũng như
và của dòng điện thì số lượng hạt tải lại ở một trạng thái cân bằng nhiệt động
riêng, do đó mà hệ số Hall cũng thay đổi theo. Vì vậy mà kết quả trên thực
nghiệm ta thấy phù hợp với lý thuyết.
IV. Kết luận
Do RH > 0 nên đây là bán dẫn loại p. Ta thấy rằng giá trị của RH giảm
dần khi từ trường tăng, hay dòng qua bán dẫn tăng.
V. Trả lời câu hỏi
Câu 1: Hiệu ứng Hall trong kim loại và hiệu ứng Hall trong bán dẫn?
1.Chuyển động của hạt mang điện trong từ trường
Một hạt có điện tích q chuyển động với vận tốc v trong từ trường
B
sẽ
chịu tác dụng của lực lorentz
,
F q v B
. Hướng của lực này phụ thuộc vào
dấu của hạt mang điện và hướng của tích
,
v B
. Nếu hướng của
v
vuông góc
với
B
thì dưới tác dụng của lực lorentz sẽ xảy ra sự lệch của các hạt theo
phương vuông góc với
v
và
B
, do đó sẽ xuất hiện sự phân bố điện tích không
gian và xuất hiện điện trường
y
. Trong trạng thái dừng, lực điện trường tác
dụng lên hạt mang điện bằng lực lorentz.
y
F qE qvB
B là cảm ứng từ: 0
B H

;
µ là độ từ thẩm
7
0
4 .10 /
H m
Hằng số từ
H: cường độ từ trường (A/ m)
Hiện tượng tạo lên từ trường Ey và làm xuất hiện một hiệu điện thế U
khi vật dẫn có dòng điện chạy qua được đặt trong từ trường gọi là hiệu ứng
Hall
2.Hiệu ứng Hall trong kim loại
Ta cho dòng điện chạy qua một bản vật dẫn với mật độ dòng
j
. Một
từ trường có cảm ứng từ
B
đặt vuông góc với
j
và vuông góc với bản. Khi đó
theo phương vuông góc với
j
và
B
, trên hai mặt bên của bản xuất hiện hiệu
điện thế: U= R j Bd
R : hằng số Hall
J : mật độ dòng
d: độ rộng của bản ( khoảng cách giữa hai bản có tồn tại hiệu điện thế)
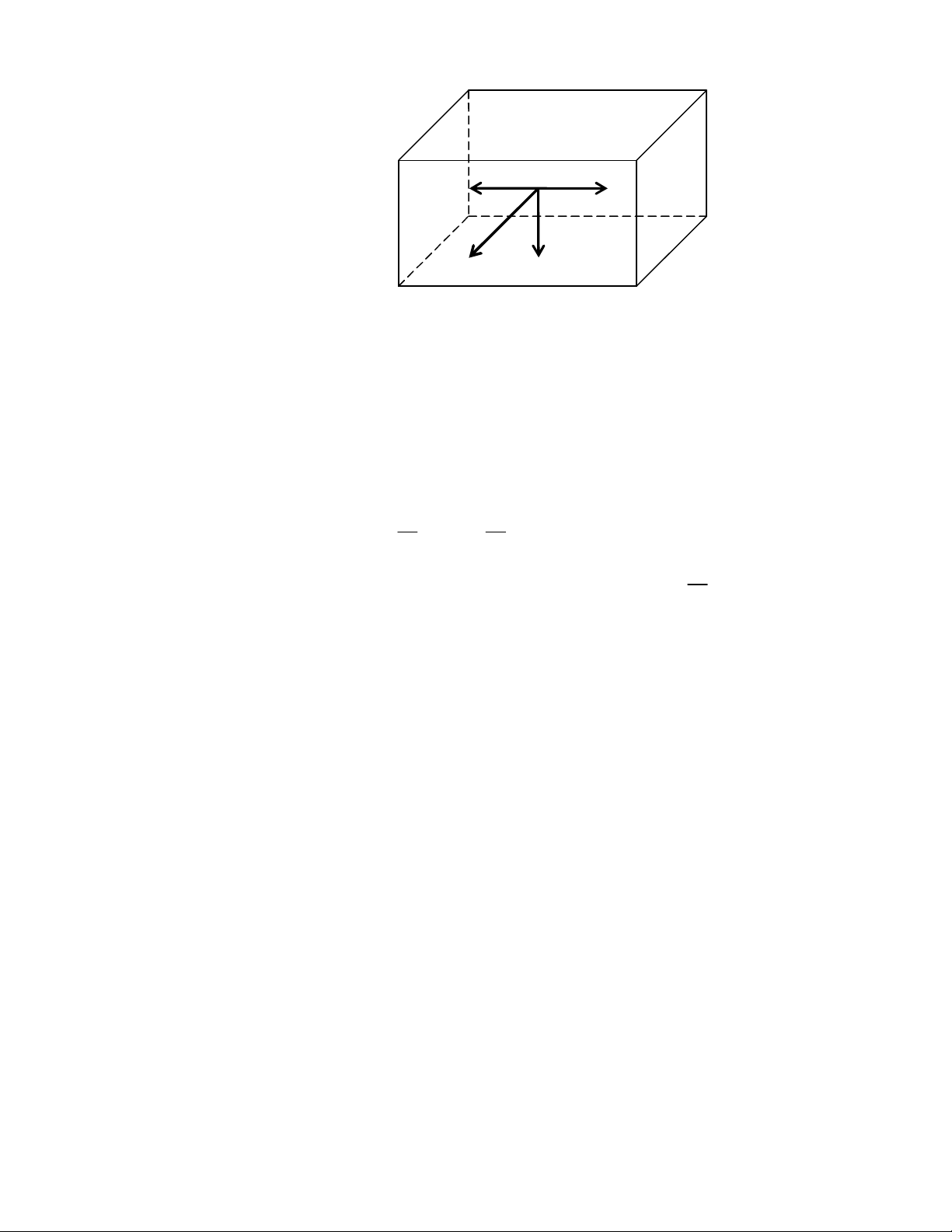
Dưới tác dụng của lực lorentz electron chuyển động xuống dưới nên
bờ dưới mang điện âm còn bờ trên mang điện dương, vì thế có sự trên lệc
điện thế giữa hai bản, làm xuất hiện điện trường
y
hướng từ trên xuống
dưới. Khi trạng thái cân bằng đạt được, lực lorentz có giá trị bằng giá trị của
lực điện trường
y
eE
(hướng lên).
y e y e
eE ev B E v B
Mà e e
j
j nv e v
ne
1
y
E jB
ne
Hiệu điện thế giữa bờ trên và bờ dưới là: 1
y
U E d jBd
ne
3.Hiệu ứng Hall trong bán dẫn
Xét dòng điện có mật độ dòng
j
chạy qua một mẫu bán dẫn hình hộp
chữ nhật có chiều dày là d. Một từ trường cảm ứng từ
B
đặt vuông góc với
j
và
vuông góc với bản.
Trong bán dẫn luôn tồn tại hai loại hạt mang điện: electron và lỗ
trống.
Mật độ dòng electron và lỗ trống được xác định.
e e
j nev
và
h h
j pev
n, p là mật độ electron và mật độ lỗ trống
e là độ lớn điện tích của electron
j
F
B
e
v
d