Baìi giaíng Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
Chæång III :
CHUYÃØN ÂÄÜNG QUAY CUÍA VÁÛT RÀÕN
XUNG QUANH MÄÜT TRUÛC CÄÚ ÂËNH
§1. Mäüt säú liãn kãút thäng duûng giæîa hai váût ràõn:
@ Cho hai váût ràõn (S) vaì (Σ) tiãúp xuïc nhau vaì cuìng chuyãøn âäüng trong hãû quy chiãúu (R). Taïc
âäüng cå tæì (Σ) lãn (S) taûi chäù tiãúp xuïc khi thu goün vãö âiãøm tiãúp xuïc A báút kyì thuäüc (S) gäöm: Læûc
thu goün vaì momen thu goün: . R
G
,
A tiepxuc
M
G
@ Täøng cäng suáút cuía caïc taïc âäüng cå tæì (Σ) lãn (S) vaì tæì (S) lãn (Σ) taûi chäù tiãúp xuïc bàòng :
S
PP P
Σ
=+
våïi: SS,
P = R. v (A) .
A tiepxuc S
M
+
Ω
GG
GG
,
P = - R. v (A) .
A tiepxuc
M
Σ
ΣΣ
−
Ω
G
GG
G
AS vaì láön læåüt laì caïc âiãøm thuäüc (S) vaì (Σ) truìng nhau taûi âiãøm A;
AΣS
v (A )
G
, láön læåüt
laì váûn täúc cuía âiãøm vaì A thuäüc (S) vaì (Σ);
v (A )
Σ
G
S
AΣS
Ω
G
,
Ω
G
láön læåüt laì veïctå quay cuía (S) vaì (Σ)
trong (R).
@ Liãn kãút giæîa (S) vaì (Σ) âæåüc goüi laì lyï tæíåíng (parfait) (khäng coï ma saït) nãúu nhæ :
0
S
PP P
Σ
=+=
@ Thäng thæåìng, chuïng ta nghiãn cæïu chuyãøn âäüng cuía váût ràõn (S) trong hãû quy chiãúu
(
)
R
Σ
gàõn
liãön våïi (Σ) ((Σ) âoïng vai troì gia âåî vaì (S) dëch chuyãøn trãn âoï). Khi âoï taïc âäüng cå tæì lãn
taûi chäù tiãúp xuïc khäng sinh cäng vç(
()S
()Σ)
Σ
cäú âënh ⇒ Täøng cäng suáút P cuía caïc taïc âäüng cå tiãúp
xuïc bàòng cäng suáút cuía taïc âäüng cå tæì
S
P ()
Σ
lãn taûi chäù tiãúp xuïc :
()S
SS/,
/
P = P = R. v (A ) .
RAtiepxucS
R
M
Σ
Σ
+Ω
GG
GG
våïi : , vectå quay cuía (S) vaì váûn täúc cuía âiãøm A thuäüc (S) trong hãû quy chiãúu
.
/
SRΣ
Ω
G
S/
v (A ) RΣ
G
RΣ
R
G
g
v
G/SR
Σ
Ω
G
R
G
,A tiepxuc
M
G
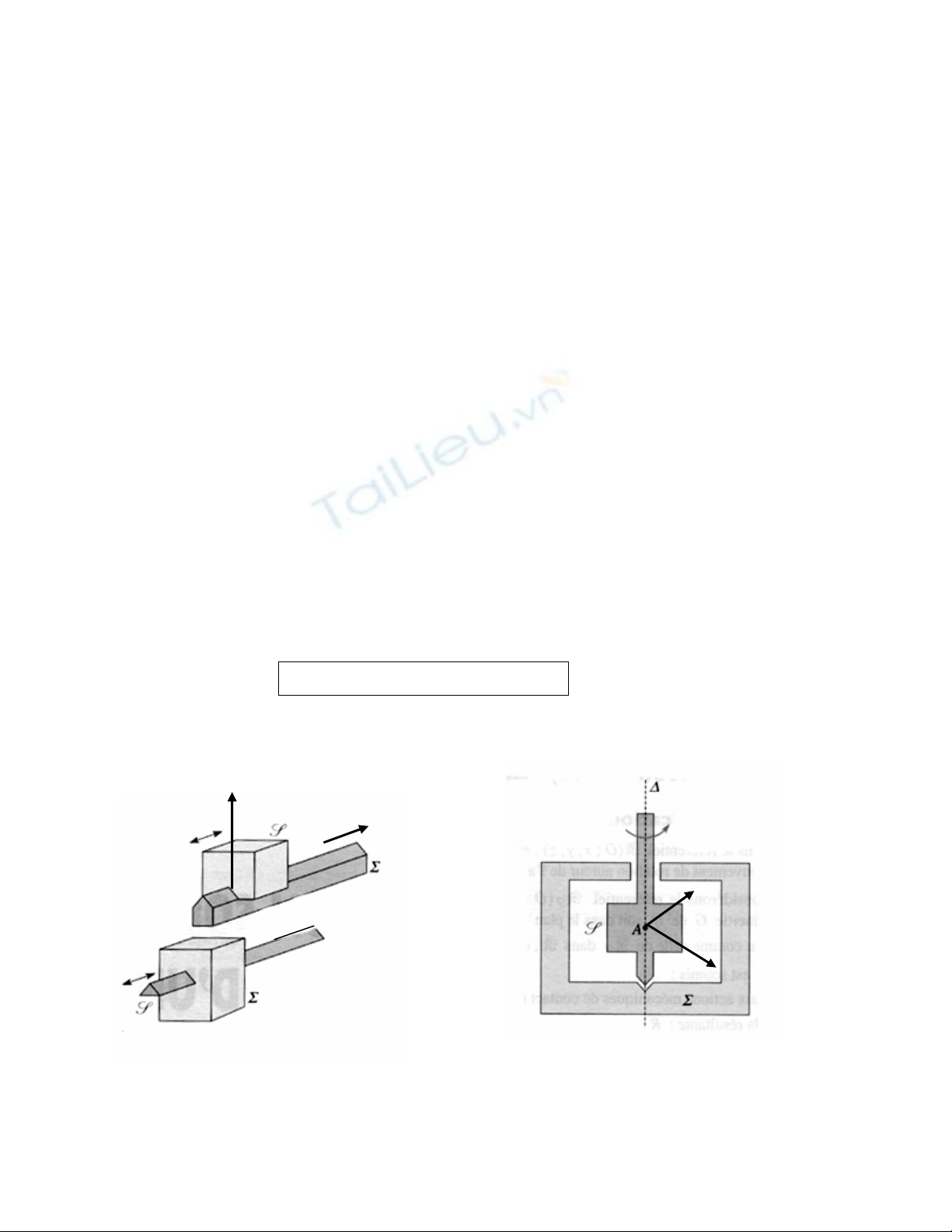
Hçnh 1 : Vê duû vãö liãn
kãút træåüt
Hçnh 2 : Vê duû vãö liãn kãút baín
lãö (liãn kãút truû quay)
28
Baìi giaíng Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
1) Liãn kãút træåüt (liãn kãút kiãøu làng truû, liãn kãút tënh tiãún):
@ Hai váût ràõn (S) vaì (Σ) âæåüc goüi laì coï liãn kãút træåüt (liason glissieìre) våïi nhau nãúu (S) chè
chuyãøn âäüng tënh tiãún thàóng song song våïi mäüt truûc gàõn liãön våïi (Σ) (Hçnh 1).
@ Liãn kãút træåüt laì lyï tæåíng (khäng coï ma saït træåüt) nãúu læûc thu goün R
G
vuäng goïc våïi phæång
chuyãøn âäüng cuía (S) trãn (Σ).
Do (S) tënh tiãún trong hãû quy chiãúu R
Σ
gàõn liãön våïi (Σ) nãn táút caïc caïc âiãøm thuäüc (S) coï cuìng
váûn täúc vaì bàòng váûn täúc træåüt v
g
Gcuía (S) trãn()
Σ
: S/
v (A ) v
R
Σg
=
G
G. Màût khaïc : ,
0
A tiepxuc
M
=
(ma
saït làn vaì ma saït xoay khäng xuáút hiãûn) Cäng suáút cuía taïc âäüng cå tæì lãn taûi chäù tiãúp
xuïc :
⇒()Σ()S
SS/g
P .v(A) .v 0
R
RR
Σ
==
GG
GG
=
(do g
R v
⊥
G
G
)
2) Liãn kãút baín lãö (liãn kãút truû quay, liãn kãút quay):
@ Hai váût ràõn (S) vaì (Σ) âæåüc goüi laì coï liãn kãút baín lãö (liason pivot) våïi nhau nãúu (S) chè chuyãøn
âäüng quay xunh quanh mäüt truûc (∆) gàõn liãön våïi (Σ) (Hçnh2).
@ Liãn kãút baín lãö laì lyï tæåíng (khäng coï ma saït) nãúu thaình pháön trãn truûc quay (∆) cuía momen thu
goün vãö mäüt âiãøm A thuäüc truûc quay (∆) bàòng 0, nghéa laì nãúu :
,
A tiepxuc
M
G
,()
A tiepxuc
M⊥∆
G
Khi âoï, cäng suáút cuía taïc âäüng cå tæì ()
Σ
lãn ( taûi chäù tiãúp xuïc:
)SS
P 0
=
vç: vaì
,/
A tiepxuc S R
MΣ
⊥Ω
GG
/
v( ) 0
SR
AΣ=
G
§2. Nghiãn cæïu chuyãøn âäüng quay (Liãn kãút baín lãö):
1) AÏp duûng âënh lyï vãö âäüng læåüng vaì momen âäüng læåüng :
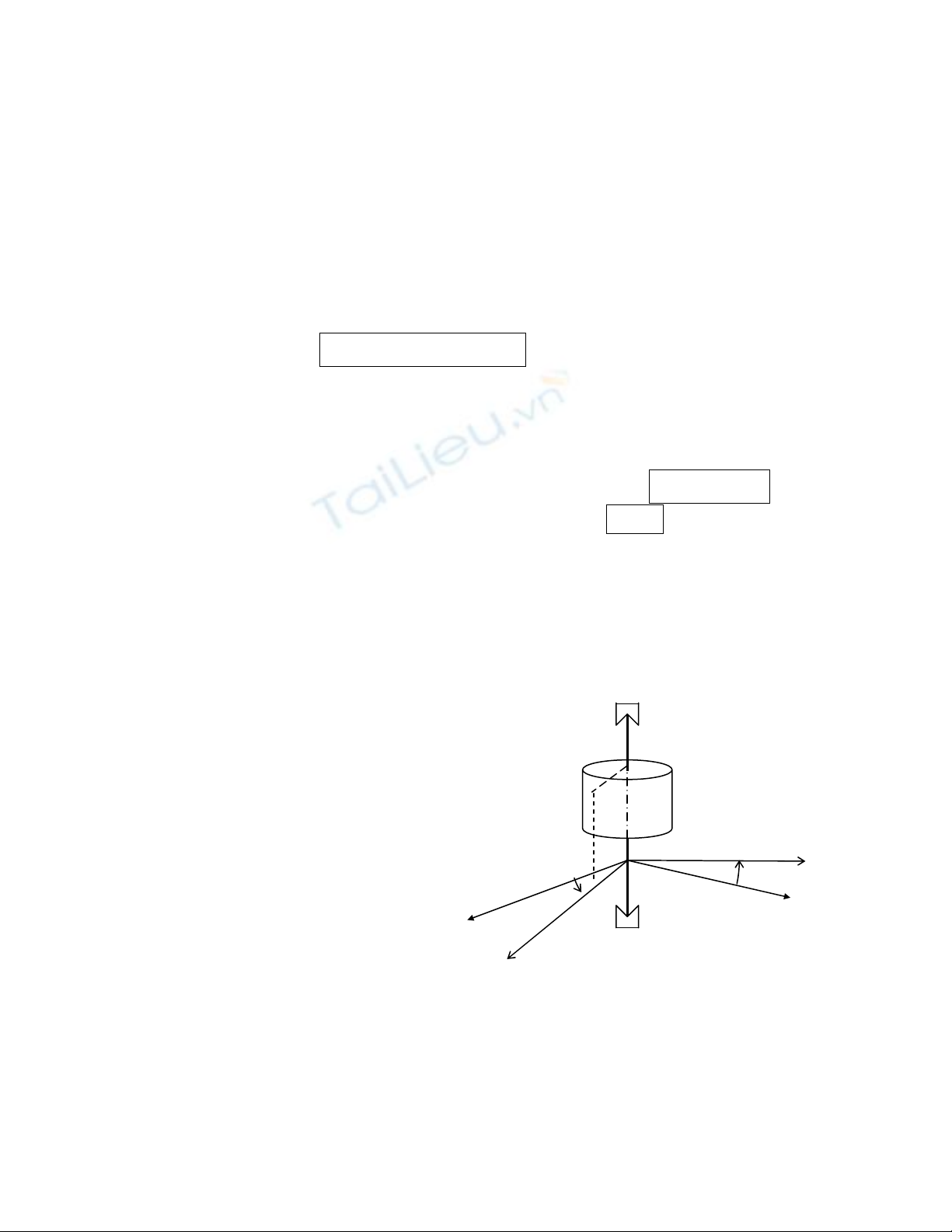
Xeït mäüt váût ràõn (S) quay xung quanh mäüt truûc cäú âënh Oz trong hãû quy chiãúu (;,,)
R
Oxyz giaí sæí
laì Galileïe. Giaí sæí ràòng liãn kãút giæîa (S) vaì
giaï cäú âënh (liãn kãút baín lãö) laì lyï tæåíng
(khäng coï ma saït).
z
Goiü (; , , )
SSSS
R
Ox y z laì hãû quy chiãúu gàõn
liãön våïi (S), sao cho khäúi tám G cuía (S)
nàòm trong màût phàóng (OxSz).
Chuyãøn âäüng quay cuía (S) trong hãû quy
chiãúu (R) âæåüc xaïc âënh bàòng goïc quay
JJ JJJJ .
S
= (Ox, Ox )
θ
JG G
R
(S) chëu taïc âäüng cuía caïc ngoaûi læûc: Taïc
âäüng cå tiãúp xuïc do caïc baín lãö taïc âäüng
lãn truûc quay, khi thu goün vãö âiãøm O
gäöm: Læûc thu goün G vaì momen thu
goün: ,
O tiepxuc
M
Oz⊥G
GJJ (do liãn kãút khäng coï ma saït); caïc ngoaûi læûc khaïc biãút træåïc (nhæ troüng læåüng,
ngáùu læûc cuìa âäüng cå...) taïc âäüng lãn (S), khi thu goün vãö âiãøm O gäöm: Læûc thu goün vaì momen
thu goün:
F
G
O
M
G
B
A
θ
y
s
y
s
x
a
H
çnh 3
θ
O
b
G
x
Âãø nghiãn cæïu chuyãøn âäüng cuía váût ràõn (S) coï thãø aïp duûng âënh lyï vãö âäüng læåüng, âënh lyï vãö
momen âäüng læåüng vaì âënh lyï vãö âäüng nàng.
29
Baìi giaíng Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
@ AÏp duûng âënh lyï vãö âäüng læåüng cho váût ràõn (S) trong hãû quy chiãúu (R)
() e
i
i
dP ma G F
dt ==
∑
GG
G ⇒()ma G F R
=
+
G
G
G
Goüi a vaì b laì toüa âäü cuía G trong cå såí xs ys zs
(e ,e ,e )
G
GG , ta coï:
2
() xs ys
aG a e a e
θ
θ
=− +
GG

G
⇒
()
2xs ys
mae ae FR
θθ
−+ =+
GG
GG

Chiãúu lãn caïc truûc: ;;
s
s
Ox Oy Ozs
ta coï:
2
0
xs xs
ys ys
zz
ma F R
ma F R
FR
θ
θ
⎧−=+
⎪=+
⎨
⎪=+
⎩
 (1)
@ Aïp duûng âënh lyï vãö momen âäüng læåüng cuía váût ràõn (S) âäúi våïi âiãøm O cäú âënh :
O
dL ()
dt
e
Oi
i
M
F=∑
GGG
⇒ Oz O ,
dL dL
dt dt O O tiepxuc
MM
⊥
+=+
GGGG våïi: ,O tiepxuc
M
Oz⊥
G
⇒ Oz O ,
dL dL
dt dt Oz O O tiepxuc
MM M
⊥⊥
+=++
GGGG G
⇒ O,
dL
dt O O tiepxuc
MM
⊥⊥
=+
GGG (2)
Våïi laì thaình pháön cuía vaì cuía
;
Oz Oz
LM
GG
O
L
G
O
M
G
song song våïi truûc Oz.
Våïi laì thaình pháön cuía vaì cuía
;
OO
LM
⊥⊥
GG
O
L
G
O
M
G
vuäng goïc våïi truûc Oz.
Vaì : Oz
dL
dt Oz
M
=
GG
Maì: Oz
LOz Oz z
JJe
θ
=Ω=
GG
G
Suy ra : Hay:
Oz z Oz
JeM
θ
=G
G
 Oz Oz
JM
θ
=
 (3)
2) Nghiãn cæïu chuyãøn âäüng cuía váût ràõn (S):
@ Nãúu cáön xaïc âënh quy luáût chuyãøn âäüng = (t)
θ
θ
cuía váût ràõn (S) coï thãø aïp duûng âënh lyï vãö
momen âäüng læåüng âäúi våïi truûc Oz cäú âënh :
dL ()
dt
e
Oz Oz i
i
M
F=∑
GGG
⇒ Oz z Oz
JeM
θ
=
G
G
 ⇒Oz Oz
J
M
θ
=
 (4)
Âáy chênh laì phæång trçnh vi phán cuía chuyãøn âäüng quay cuía (S).
@ Coï thãø viãút phæång trçnh vi phán cuía chuyãøn âäüng quay cuía (S) bàòng caïch aïp duûng âënh lyï
âäüng nàng: int
dE
dt
ext
ki
ii
PP=+
∑∑
i
. Våïi : vaì láön læåüt laì cäng suáút cuía ngoaûi læûc
ext
i
Pint
i
Pe
i
F
G
vaì
näüi læûc taïc âäüng lãn (S) ⇒
i
i
F
G2
d1
dt 2 tiepxuc khac
JPP
θ
⎛⎞
=+
⎜⎟
⎝⎠
30
Baìi giaíng Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
Trong âoï: laì cäng suáút cuía taïc âäüng cå lãn (S) taûi chäù tiãúp xuïc, laì cäng suáút cuía caïc
ngoaûi læûc khaïc taïc âäüng lãn (S).
tiepxuc
Pkhac
P
Do liãn kãút baín lãö laì lyï tæåíng: 0
tiepxuc
P
=
Màût khaïc : .v( )
khac O z Oz
PFOMeM
θ
θ
=+=
GG
GG

⇒ Oz Oz
JM
θ
θθ
=
 ⇒ Oz Oz
JM
θ
=
 (5)
3) Taïc âäüng cå tiãúp xuïc:
Khi biãút quy luáût chuyãøn âäüng = (t)
θ
θ
, coï thãø xaïc âënh âæåüc taïc âäüng cå lãn (S)
taûi chäù tiãúp xuïc nhåì caïc phæång trçnh (1), (2) .
,
(R, )
O tiepxuc
M
GG
4) Âënh luáût baío toaìn momen âäüng læåüng âäúi våïi truûc quay:
Khi caïc ngoaûi læûc taïc duûng lãn váût ràõn quay xung quanh mäüt truûc cäú âënh coï momen âäúi våïi truûc
quay bàòng 0, momen âäüng læåüng cuía váût ràõn âäúi våïi truûc quay âæåüc baío toaìn.
Tháût váûy, theo âënh lyï vãö momen âäüng læåüng: Oz
dL ()
dt
e
Oz i
i
M
F=∑
G
G
G
Maì: .Suy ra:
()0
e
Oz i
i
MF=
∑GG Oz
dL 0
dt
=
G
. Hay: Oz
Lconst=
J
JJJJG
G
Tµi liÖu tham kh¶o :
[1] C¬ häc vËt r¾n, N¨m thø hai, MP-MP*-PC-PC*-PT-PT*, Hachette SupÐrieure, Nxb. Gi¸o
dôc Hµ Néi 2002
[2] MÐcanique des solides, DeuxiÌme annÐe, MP-MP*-PC-PC*-PT-PT*, Hachette SupÐrieure,
1999
[3] L−¬ng Duyªn B×nh (chñ biªn), VËt lý ®¹i c−¬ng, TËp I : C¬- NhiÖt, Nxb. Gi¸o dôc Hµ Néi
1998
31