Baìi giaíng Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
Chæång 2 :
TIÃÚP XUÏC GIÆÎA HAI VÁÛT RÀÕN - ÂËNH LUÁÛT VÃÖ MA SAÏT
§1. Nghiãn cæïu âäüng hoüc:
(R)
xO
y
(
Σ
)
(S)
(
Σ
)
I
H
çnh 1:
S/R
v(I )
G
/R xe
v(I ) v
∑
=
GG
g
v(I)
G
z
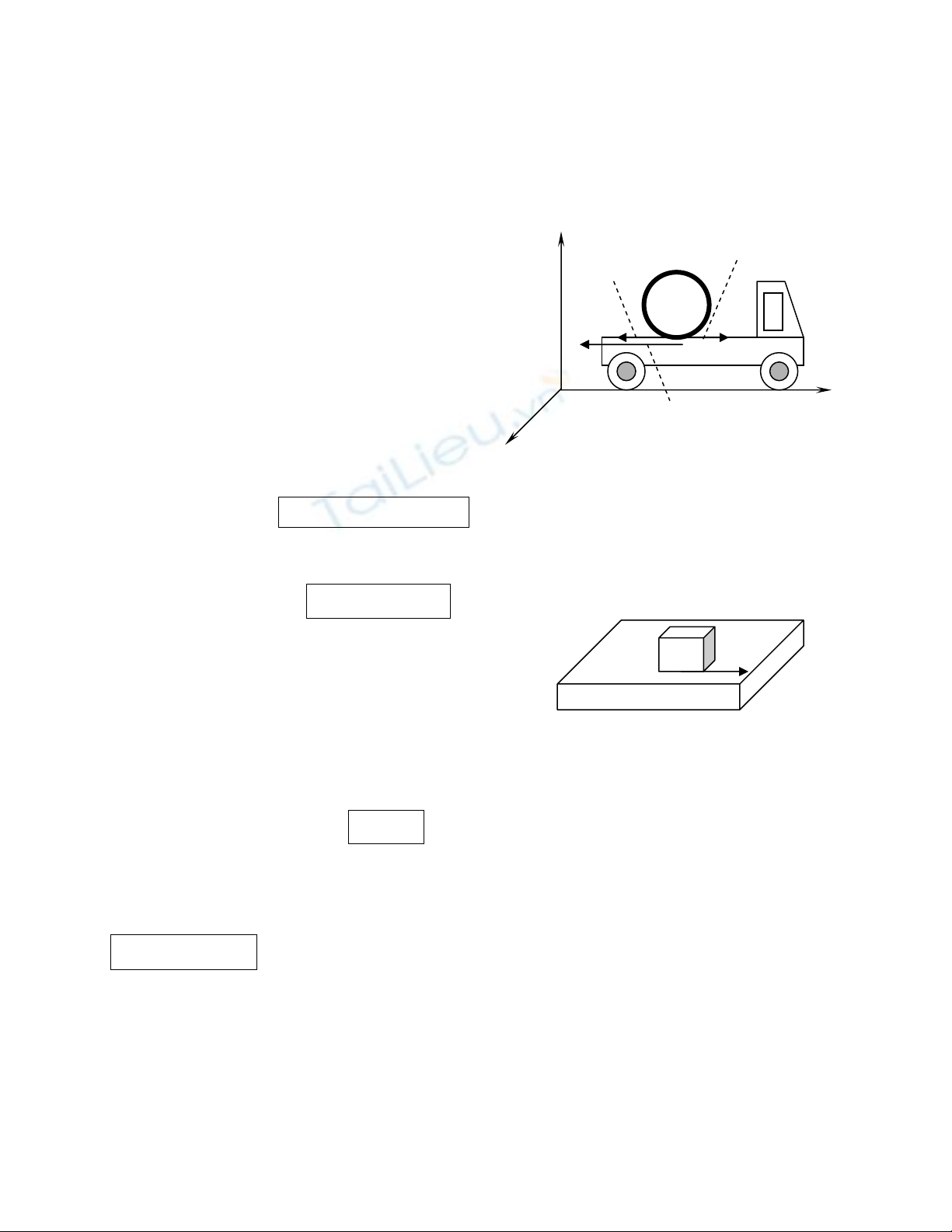
1) Váûn täúc træåüt:
• Xeït hai váût ràõn (S) vaì (Σ) luän luän tiãúp xuïc
våïi nhau, vaì cuìng chuyãøn âäüng trong hãû quy
chiãúu R (Hçnh 1).
Chuïng coï thãø tiãúp xuïc theo mäüt màût, theo mäüt
âæåìng hay theo mäüt âiãøm Taûi mäùi thåìi âiãøm
t, luän luän coï êt nháút mäüt âiãøm IS cuía (S) truìng
våïi mäüt âiãøm IΣ cuía (Σ) taûi âiãøm tiãúp xuïc I.
⇒
Váûn täúc træåüt v
g
K cuía (S) trãn (Σ) taûi âiãøm I vaìo
thåìi âiãøm t :
//
v() v( ) v( )
g
SR R
II I
∑
=−
KK K
Váûn täúc træåüt cuía (S) trãn (Σ) taûi âiãøm I cuîng chênh laì váûn täúc cuía âiãøm IS cuía (S) (hçnh truû) trong
hãû quy chiãúu ()
R
∑ gàõn liãön våïi (Σ) (xe cam nhäng) :
/
v() v( )
g
SR
II
∑
=
KK
g
v(I)
G
(P)
()
∑
(S)
H
çnh 2
• Thäng thæåìng, chuïng ta nghiãn cæïu chuyãøn âäüng cuía
váût ràõn (S) trãn mäüt giaï âåî (Σ) cäú âënh trong hãû quy chiãúu
R : Khi âoï hãû quy chiãúu ()
R
∑ truìng våïi hãû quy chiãúu R.
• Trong træåìng håüp giæîa hai váût ràõn (S) vaì (Σ) täön taûi
mäüt tiãúp diãûn chung (P), váûn täúc træåüt v
g
K
seî nàòm trong
màût phàóng (P) (Hçnh 2).
• (S) âæåüc goüi laì khäng træåüt trãn (Σ) khi váûn täúc træåüt bàòng 0 taûi moüi âiãøm tiãúp xuïc I :
v() 0
gI
=
G
K
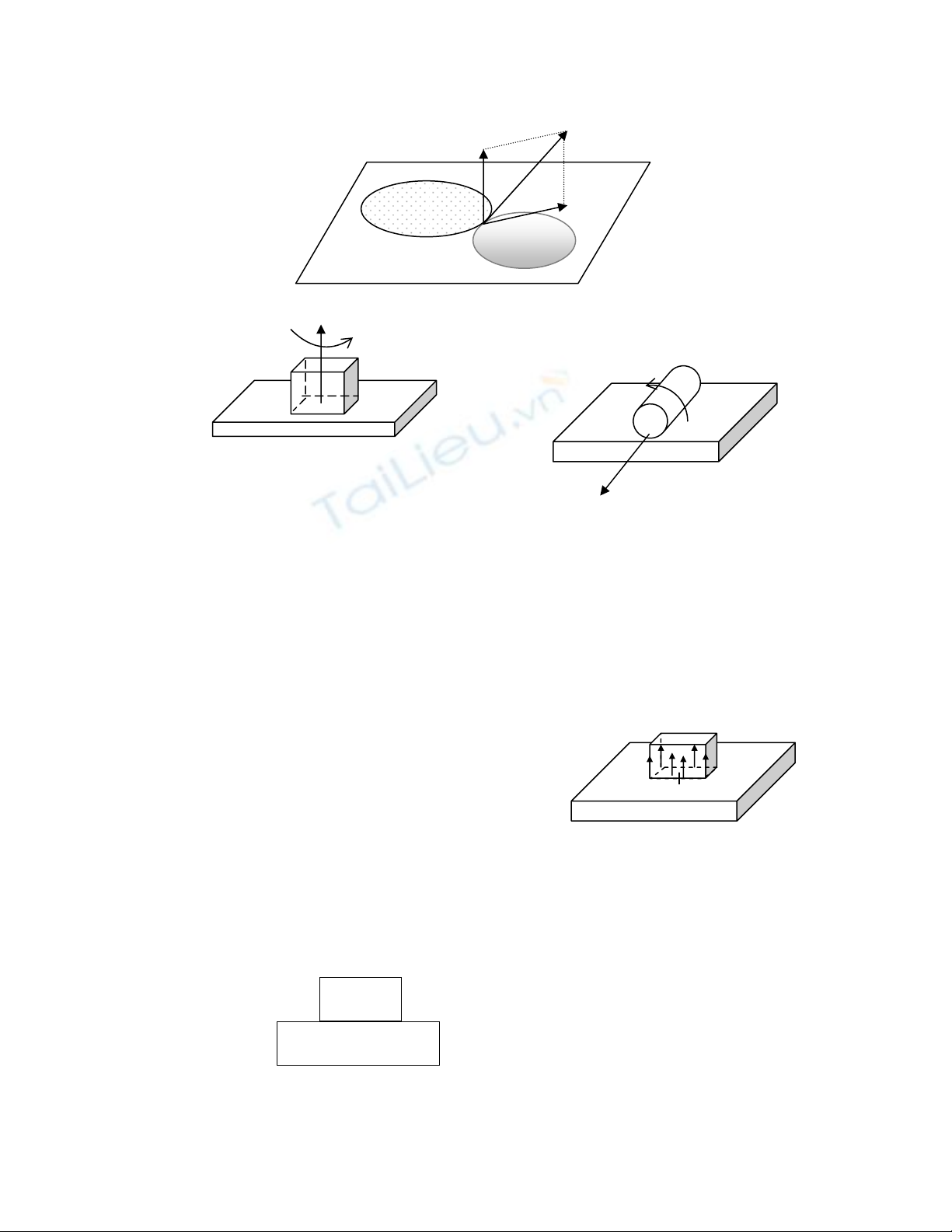
2) Chuyãøn âäüng làn vaì xoay cuía (S) âäúi våïi (Σ):
• Trong hãû quy chiãúu R, goüi vaì
S
Ω
K
∑
Ω
K
laì vectå quay cuía váût ràõn (S) vaì (Σ). Veïctå quay tæång
âäúi cuía (S) so våïi (Σ), tæïc laì veïctå quay cuía (S) trong hãû quy chiãúu
/S∑
Ω
K()
R
∑ gàõn liãön våïi (Σ):
/SS∑
Ω=Ω−Ω
KK
∑
K
coï thãø âæåüc phán thaình hai thaình pháön (Hçnh 3).
+ Veïctå phaïp
N
Ω
Kvuäng goïc våïi tiãúp diãûn chung taûi I cuía (S) vaì (Σ).
(P)
N
Ω
K âæåüc goüi laì vectå
quay cuía chuyãøn âäüng xoay.
+ Veïctå tiãúp nàòm trong tiãúp diãûn chung .
T
Ω
K(P) T
Ω
K
âæåüc goüi laì vectå quay cuía chuyãøn âäüng
làn.
21
Baìi giaíng Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
22
(P)
(
Σ
)
(S)
I
N
Ω
G
T
Ω
G
/S
∑
Ω
G
H
çnh 3:
H
çnh 5: Hçnh truû (S) chuyãøn âäüng
làn so våïi giaï âåî
T
Ω
=Ω
K
K
()
∑
()S
I
N
Ω=Ω
KK
()∑
()S
I
H
çnh 4 : Khäúi vuäng (S) chuyãøn
âäüng xoay so våïi giaï âåî
• Trong toaìn bäü pháön Cå hoüc váût ràõn, chuïng ta chè nghiãn cæïu caïc chuyãøn âäüng âån giaín cuía váût
ràõn (S) trãn giaï âåî cäú âënh våïi:
()∑
+ Caïc vectå
N
Ω
K vaì khäng thay âäøi phæång trong quïa trçnh chuyãøn âäüng.
T
Ω
K
+ (S) làn khäng xoay ( ) hay xoay khäng làn (
0
N
Ω=
K0
T
Ω
=
K
), hoàûc khäng làn khäng xoay
(chuyãøn âäüng tënh tiãún) trãn
()∑
§2. Taïc âäüng cå taûi chäù tiãúp xuïc:
1) Taïc âäüng cå taûi chäù tiãúp xuïc cuía hai váût ràõn:
()
∑
()S
I
i
R
G
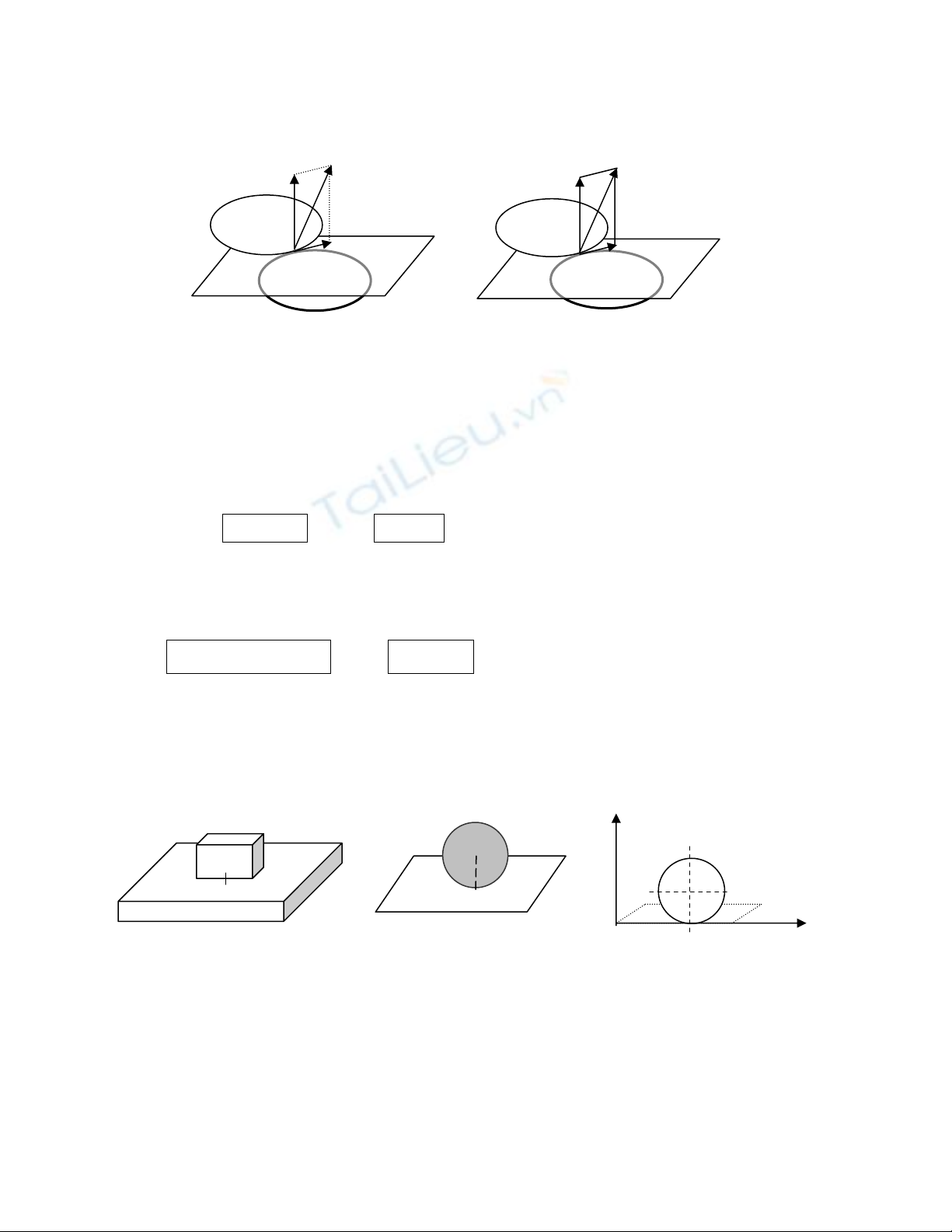
@ Hai váût ràõn (S) vaì (Σ) coï thãø tiãúp xuïc nhau theo màût
(khäúi vuäng tiãúp xuïc våïi màût phàóng), theo âæåìng (hçnh
truû tiãúp xuïc våïi màût phàóng) hay theo âiãøm (hçnh cáöu
tiãúp xuïc våïi màût phàóng). Tuy nhiãn, trãn thæûc tãú, do coï
biãún daûng âaìn häöi, (S) vaì (Σ) luän tiãúp xuïc nhau theo
mäüt màût naìo âoï (diãûn têch tiãúp xuïc coï thãø khaï nhoí).
H
çnh 6:
Taïc âäüng cå taûi chäù tiãúp xuïc giæîa (S) vaì (Σ) gáy ra båíi tæång taïc giæîa caïc phán tæí cuía (S) vaì (Σ)
trãn bãö màût tiãúp xuïc, vaì coï táöm taïc duûng ráút ngàõn. Noïi chung, âáy laì mäüt hãû læûc khäng gian phán
bäú (Hçnh 6).
@ Taïc âäüng cå tæì (Σ) lãn (S) taûi chäù tiãúp xuïc, khi thu goün vãö mäüt âiãøm tiãúp xuïc I, bao gäöm:
• Læûc thu goün (Håüp læûc): i
i
R = R
∑
GG
• Momen thu goün: I, tiepxuc
M(
Ii
i
)
M
R=∑
G
GG
Theo âënh luáût III Newton, (S) seî taïc duûng lãn (Σ) mäüt hãû læûc, khi thu goün vãö I cuîng bao gäöm:
G
• Læûc thu goün: - R
Baìi giaíng Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
• Momen thu goün: I, tiepxuc
- M
G
Taïc âäüng cå taûi chäù tiãúp xuïc laì áøn säú cuía baìi toaïn phán têch læûc.
@ Taïc âäüng cå do (Σ) taïc duûng lãn (S) taûi chäù tiãúp xuïc âæåüc phán thaình caïc thaình
pháön (Hçnh 7) :
I, tiepxuc
(R, M )
GG
• Âäúi våïi håüp læûc : R
G
+ Thaình pháön nòm taûi I trong tiãúp diãûn chung (P) taûi I cuía (S) vaì (Σ). T
G
+ Thaình pháön nòm taûi I theo phæång phaïp tuyãún taûi I våïi (P)
N
G
R = T + N
GGG
våïi: T N⊥
G
G
• Âäúi våïi momen :
I, tiepxuc
M
G
+ Thaình pháön nàòm trong tiãúp diãûn chung (P).
I,
Mt
G
+ Thaình pháön nàòm theo phæång phaïp tuyãún våïi (P) .
I,
Mn
G
I, tiepxuc I, I,
M = MM
tn
+
GGG
våïi : I, I,
MM
tn
⊥
G
G
N
Gâæåüc goüi laì aïp læûc (phaín læûc phaïp tuyãún); T
G
âæåüc goüi laì læûc ma saït træåüt båíi vç noï chäúng laûi
chuyãøn âäüng træåüt cuía (S) trãn (Σ); I,
Mt
G
âæåüc goüi laì momen ma saït làn båíi vç noï chäúng laûi
chuyãøn âäüng làn cuía (S) trãn (Σ); I,
Mn
G
âæåüc goüi laì momen ma saït xoay båíi vç noï chäúng laûi
chuyãøn âäüng xoay cuía (S) trãn (Σ).
@ Trong chæång naìy, chuïng ta seî boí qua ma saït xoay vaì ma saït làn. Båíi vç chuïng ta chè nghiãn cæïu caïc
træåìng håüp âån giaín :
+ Hoàûc: (S) chuyãøn âäüng tënh tiãún trãn giaï âåî (Σ) nhæ hçnh 9, momen ma saït xoay vaì momen ma saït làn
khäng xuáút hiãûn.
+ Hoàûc : (S) tiãúp xuïc våïi giaï âåî (Σ) theo âiãøm (hçnh cáöu tiãúp xuïc våïi màût phàóng - hçnh 10, hay træåìng håüp
tiãúp xuïc theo âæåìng trong baìi toaïn phàóng : Baïnh xe làn trãn màût âáút - hçnh 11), chuïng ta boí qua ma saït làn
vaì ma saït xoay.
I, n
M
G
(P)
()
Hçnh 8:
Σ
(S)
I, tiepxuc
M
G
I, t
M
G
N
G
(P)
I T
G
R
G
(S)
()
Σ
Hçnh 7:
()∑
I
()S
I
(
Σ
)
(
S
)
H
çnh 11
I
x
O
y
H
çnh 10
Hçnh 9
23
Baìi giaíng Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
Khi âoï, taïc âäüng cå taûi chäù tiãúp xuïc tæì váût ràõn (Σ) lãn váût ràõn (S) chè coìn laûi håüp læûc R = T + N
GGG
âi qua
âiãøm tiãúp xuïc I.
2) Âënh luáût Coulomb vãö ma saït træåüt (khä) :
Khi nghiãn cæïu chuyãøn âäüng cuía váût ràõn, phaíi kãø thãm vaìo caïc áøn säú cuía baìi toaïn caïc læûc ma saït træåüt T
G
vaì aïp læûc . Caïc âënh lyï cå baín khäng cho ta âuí säú phæång trçnh âãø xaïc âënh táút caí caïc áøn säú ⇒ Do váûy,
cáön phaíi biãút thãm quan hãû giæîa vaì .
N
G
T
GN
G
Bàòng thæûc nghiãûm, Coulomb âaî tçm âæåüc mäúi quan hãû giæîa læûc ma saït træåüt vaì aïp læûcT
GN
G
.
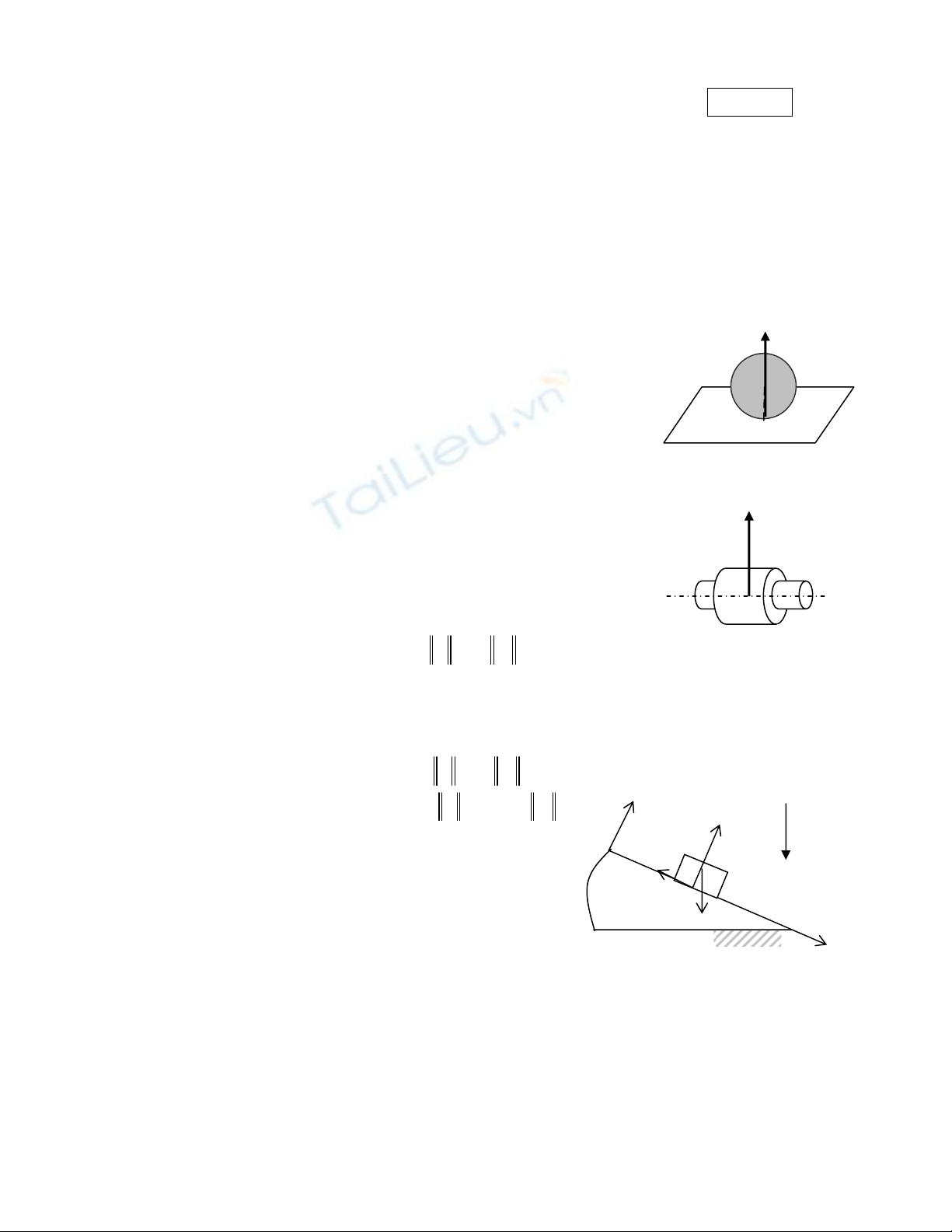
a) Tênh cháút cuía aïp læûc :
N
G
• Âäúi våïi liãn kãút mäüt phêa, vê duû khi (S) âæåüc âàût trãn giaï âåî (Σ)
(Hçnh 12), aïp læûc tæì (Σ) taïc duûng lãn (S) luän luän hæåïng tæì (Σ)
vãö (S).
N
G
(
S
)
H
çnh 12
(
Σ
)
I
N
G
N
G
(
S
)
(
Σ
)
O
O
H
çnh 13
(S) vaì (Σ) khäng tiãúp xuïc våïi nhau næîa khi: N = 0
G
• Âäúi våïi liãn kãút hai phêa, vê duû hçnh truû räùng (S) läöng qua mäüt
thanh hçnh truû (Σ) (Hçnh 13), càõt truûc OO cuía hçnh truû, nhæng
chæa thãø kãút luáûn gç vãö phæång, chiãöu cuía
N
G
N
G
.
G
b) Tênh cháút cuía læûc ma saït træåüt T:
• Tuìy theo (S) træåüt hay khäng træåüt trãn (Σ) maì T
G
coï caïc tênh
cháút khaïc nhau. Goüi váûn täúc træåüt cuía (S) trãn (Σ).
g
v
G
+ Nãúu (S) træåüt trãn (Σ): :
g
v0≠
GT
G
vaì g
v
G
song song vaì ngæåüc
chiãöu nhau: vaì
g
T v 0×=
GG
g
T .v 0<
GG
Suáút (moâun) cuía T tè lãû våïi suáút cuía
GN
G
: .TfN=
G
G
våïi f laì hãû säú tè lãû vaì âæåüc goüi laì hãû säú ma saït træåüt (f > 0).
+ Nãúu (S) khäng træåüt trãn (Σ), maì chè coï xu hæåïng træåüt trãn (Σ): g
v0
=
G
: cuìng phæång vaì
ngæåüc chiãöu våïi chiãöu cuía xu hæåïng træåüt.
T
G
Suáút cuía vaì cuía thoía maîn biãøu thæïc: T
GN
G.TfN≤
G
G
Trong caí hai træåìng håüp, giaï trë cæûc âaûi cuía T
G
bàòng .
f
N
G
• Khi f = 0, tiãúp xuïc giæîa (S) vaì (Σ) âæåüc goüi laì tiãúp xuïc
khäng coï ma saït. Khi âoï: vaì håüp læûc
T = 0
GR = T + N = N
G
GGG
vuäng goïc våïi tiãúp diãûn chung (P) taûi âiãøm tiãúp xuïc I cuía
(S) vaì (Σ).
• Vê duû, khi hçnh khäúi chæî nháût (S) âæåüc âàût nàòm yãn trãn
màût phàóng nghiãng (Σ) (Hçnh 14), (S) coï xu hæåïng træåüt
xuäúng trãn màût phàóng nghiãng (Σ) theo phæång chiãöu x'x
J
JJG ⇒T
G
hæåïng lãn theo phæång
chiãöu . xx'
JJG
N
G
g
G
mg
G
T
G
y
x’
x
H
çnh 14
Khi hçnh khäúi chæî nháût (S) cán bàòng, ta coï :
0xy
Te Ne mg=+ +
GG G
24
Baìi giaíng Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
Tæì âoï : sin 0Tmg
α
=− < vaì cos 0Nmg
α
=>
(T vaì N laì caïc gêa trë âaûi säú cuía læûc ma saït vaì cuía
aïp læûc).
c) Tênh cháút cuía hãû säú ma saït træåüt f:
• Hãû säú ma saït træåüt f phuû thuäüc vaìo:
+ Baín cháút cuía caïc váût ràõn tiãúp xuïc (váût liãûu caïc bãö màût tiãúp xuïc), vê duû khi váût ràõn bàòng theïp tiãúp xuïc våïi
váût ràõn bàòng gäù, hãû säú ma saït f seî khaïc våïi træåìng håüp váût ràõn bàòng theïp tiãúp xuïc våïi váût ràõn bàòng cao su.
+ Traûng thaïi caïc bãö màût tiãúp xuïc, vê duû khi hai bãö màût tiãúp xuïc gäö ghãö, f seî låïn. Khi hai bãö màût tiãúp xuïc
âæåüc phuí mäüt låïp cháút bäi trån, f seî giaím xuäúng.
+ Tàng theo thåìi gian tiãúp xuïc ban âáöu (thåìi gian coï aïp læûc N
G
nhæng chæa coï træåüt tæång âäúi hay xu
hæåïng træåüt tæång âäúi).
• Hãû säú ma saït træåüt f khäng phuû thuäüc vaìo diãûn têch tiãúp xuïc vaì háöu nhæ khäng phuû thuäüc vaìo váûn täúc
træåüt.
Ghi chuï: Âënh luáût Coulomb chè phaín aïnh gáön âuïng quy luáût ma saït træåüt khä, tuy nhiãn váùn coï thãø aïp
duûng noï trong nhiãöu baìi tênh kyî thuáût. Trãn thæûc tãú, f khäng phaíi laì hoaìn toaìn âäüc láûp våïi váûn täúc træåüt:
Træåìng håüp (S) khäng træåüt trãn (Σ), f låïn hån trong træåìng håüp (S) træåüt trãn (Σ), do váûy ngæåìi ta phán
biãût hãû säú ma saït âäüng fâ khi (S) træåüt trãn (Σ) vaì hãû säú ma saït ténh ft khi (S) khäng træåüt trãn (Σ). Trong
âa säú træåìng håüp: fâ < ft
2) Mäüt säú hãû quaí cuía âënh luáût Coulomb:
a) Váût ràõn cán bàòng: y
@ Hãû ngoaûi læûc taïc duûng lãn váût ràõn (S) khi thu
goün vãö âiãøm A naìo âoï bao gäöm læûc thu goün e xt
F
G
vaì momen thu goün . Trong hãû quy chiãúu
Rg giaí sæí laì hãû quy chiãúu Galileïe, váût ràõn (S) cán
bàòng khi :
A, ext
M
G
e xt
F0=
G; A, ext
M0=
G vaì nãúu váût ràõn
âæïng yãn taûi thåìi âãøm ban âáöu.
Ngoaìi ra, nãúu (S) chëu taïc âäüng cå I, tiepxuc
(R, M )
G
G
taûi âiãøm tiãúp xuïc I, thç hãû læûc naìy phaíi tuán theo âënh luáût Coulomb.
I, tiepxuc
(R, M )
GG
F
G
x’
()
Σ
mg
G
I
N
G
T
G
G
(S)
O
x
H
H
çnh 15
@ Vê duû: Khäúi chæî nháût (S) tiãúp xuïc våïi màût âáút (Σ) (Hçnh 15). Hãû ngoaûi læûc taïc duûng lãn (S)
bao gäöm: Troüng læåüng ; læûc keïo
mg
GF
G
vaì taïc âäüng cå tiãúp
xuïc tæì (Σ) lãn (S) : .
I, tiepxuc
(R, M )
GG
N
G
H
çnh 1
6
T
G
R
G
α
ϕ
(,)NR
α
=
G
G
()
Σ
Noïn (N)
(S)
Dæåïi taïc duûng cuía , giaí sæí váût ràõn (S) coï xu hæåïng chuyãøn
âäüng so våïi (Σ) theo phæång chiãöu xx’ (nhæng chæa chuyãøn
âäüng tæång âäúi so våïi (Σ)) hæåïng theo chiãöu x’x. Ta
coï:
F
G
⇒T
G
• ; T =
N = - mg
GG - F
GG
(S) khäng træåüt trãn màût âáút: TfN≤
GG
⇒F fmg≤
G
• ,
IG IH ( ) 0
I tiepxuc
mg F II T N M×+×+×++ =
JJG JJG JJG
G
GGGG
G
25







![Bài tập Vật lý sóng: Tổng hợp bài tập 6 [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250805/oursky04/135x160/401768817575.jpg)














