Baìi giaíng Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
Chæång 1 :
CHUYÃØN ÂÄÜNG CUÍA VÁÛT RÀÕN
§1. Váût ràõn trong cå hoüc :
1) Khaïi niãûm vãö váût ràõn :
Trong cå hoüc, váût ràõn laì mäüt váût thãø khäng biãún daûng : Khoaíng caïch
giæîa hai âiãøm báút kyì cuía váût ràõn khäng âäøi theo thåìi gian.
Khaïi niãûm váût thãø khäng biãún daûng chè laì mäüt mä hçnh. Vç váûy, mäüt tåì giáúy
moíng træåüt trãn màût baìn vaì khäng bë biãún daûng váùn coï thãø xem nhæ laì mäüt váût
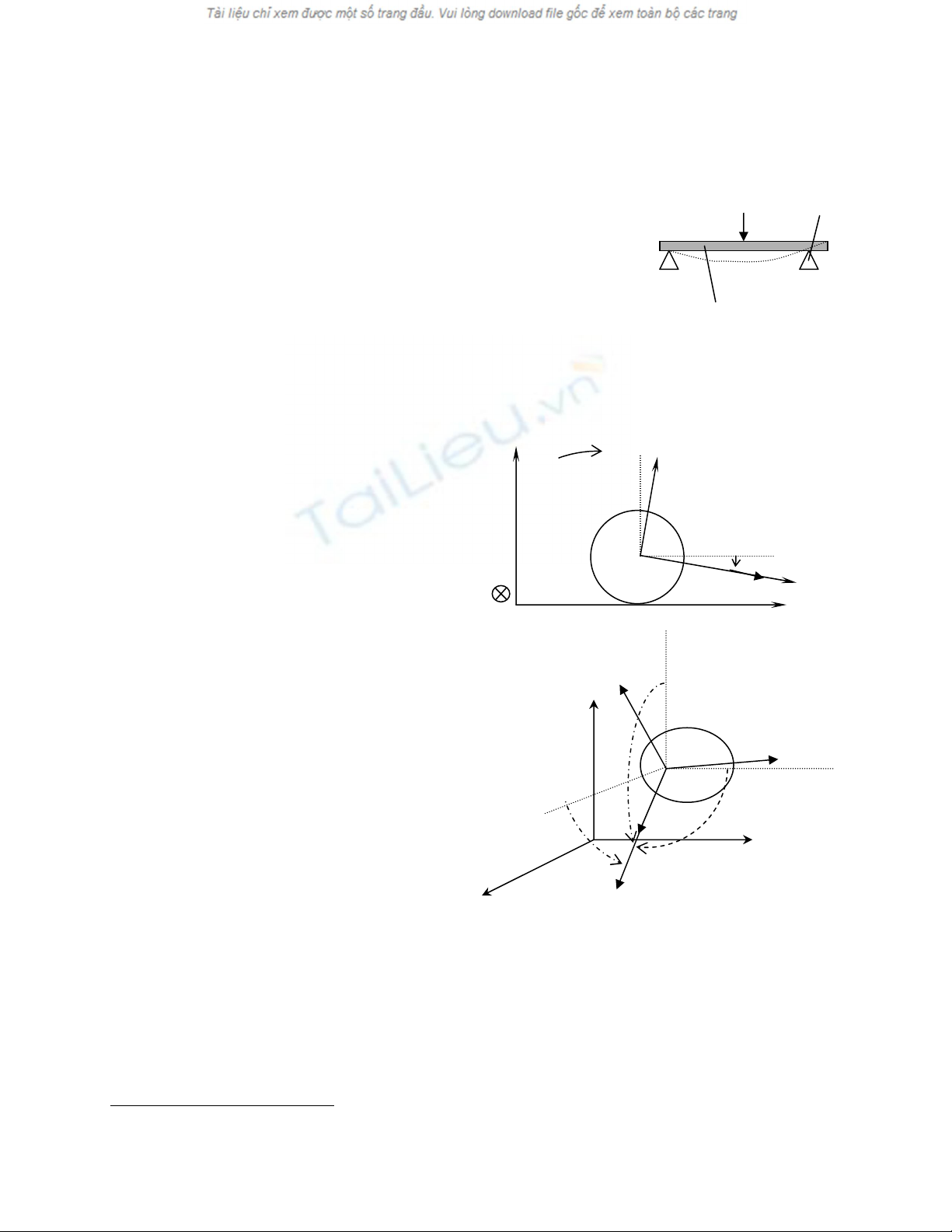
ràõn. Trong khi âoï mäüt dáöm kim loaûi âàût trãn hai gäúi tæûa vaì chëu læûc
J
G
F khaï låïn,
seî bë biãún daûng khaï nhiãöu trong quïa trçnh chëu læûc trong træåìng håüp naìy, khäng thãø coi dáöm laì váût ràõn. ⇒
F
Ggäúi tæû
a
dáöm kim loaûi
Hçnh 1
2) Hãû quy chiãúu gàõn liãön våïi váût ràõn :
(R)
S
(R )
z
x
OHçnh 2
zS
OSyS
xS
()S
O
z
y
(R)
()
S
R
xs
e
G
β
α
γ
x
M
zS
xS
C
y = yS
⊕
θ
xs
e
G
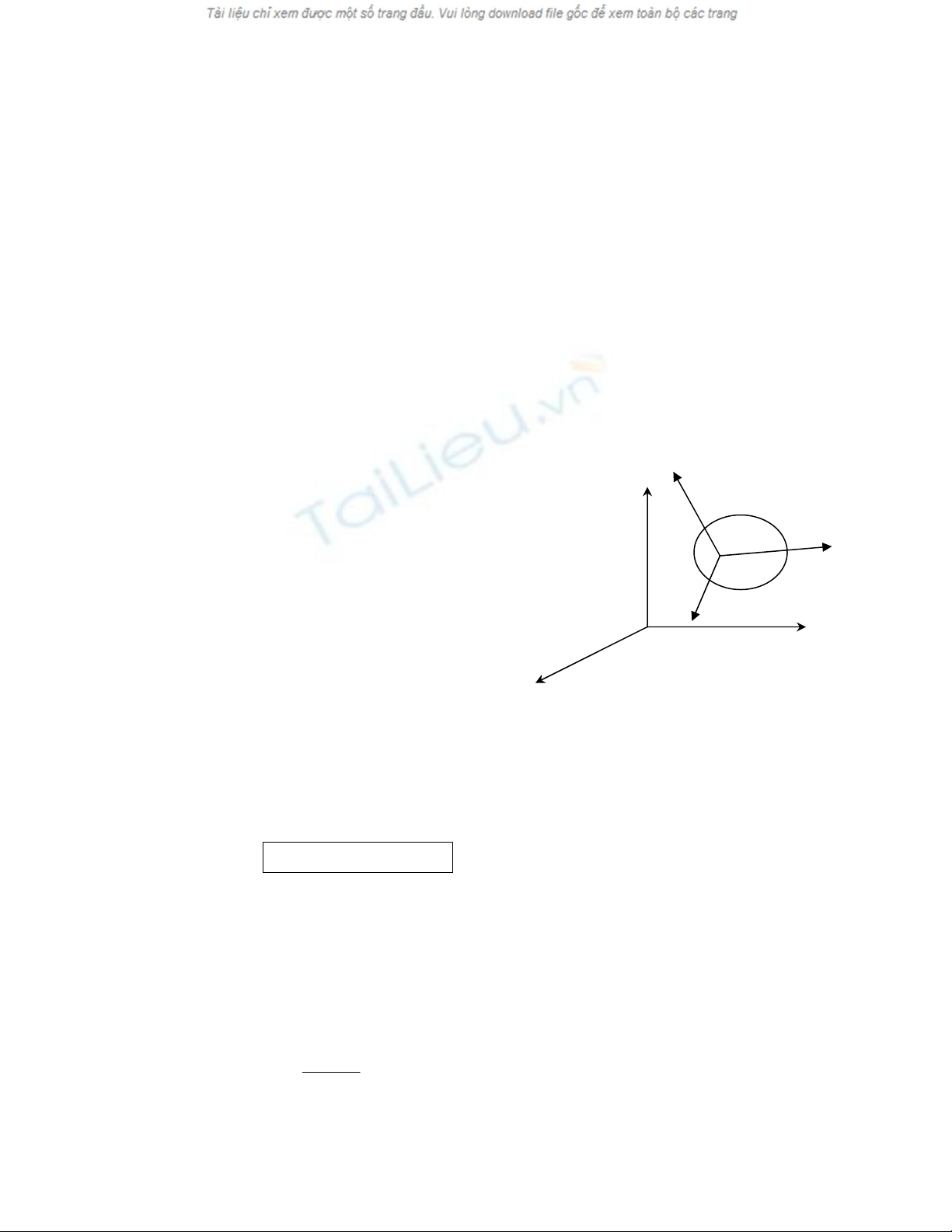
Xeït mäüt váût ràõn (S) coï daûng hçnh vaình troìn,
tám C, chuyãøn âäüng trong màût phàóng thàóng
âæïng trãn màût âáút nàòm ngang, trong hãû quy
chiãúu traïi âáút (;; ;)
x
yz
R
Oe e e
GGG. Âiãøm C, tám
cuía vaình troìn, cuîng coï thãø xem nhæ laì mäüt
âiãøm thuäüc váût ràõn, màûc âáöu taûi C khäng coï váût
cháút, båíi vç khi vaình troìn chuyãøn âäüng, âiãøm C
cuîng chuyãøn âäüng cuìng våïi vaình troìn. Täøng
quaït hån, moüi âiãøm trong khäng gian (màûc dáöu
taûi âoï khäng coï váût cháút), liãn kãút chàût cheî våïi
(S) vaì chuyãøn âäüng cuìng våïi (S) cuîng coï thãø
xem laì caïc âiãøm thuäüc váût ràõn (S).
Nhæ váûy nãúu gàõn cæïng trãn váût ràõn (S) mäüt hãû
quy chiãúu (; ; ; )
SSS
Sxyz
R
Ce e e
GGG(1) liãn kãút chàût
cheî våïi váût ràõn vaì chuyãøn âäüng cuìng våïi váût
ràõn. Khi âoï, chuyãøn âäüng cuía váût ràõn (S) trong
hãû quy chiãúu (R) coï thãø xem nhæ tæång âæång
våïi chuyãøn âäüng cuía hãû quy chiãúu (RS) so våïi
hãû quy chiãúu (R).
Hçnh 3
3) Thäng säú cáön thiãút âãø mä taí chuyãøn âäüng cuía váût ràõn :
• Âäúi våïi mäüt hãû cháút âiãøm (S) gäöm n cháút âiãøm Mi. Âãø mä taí chuyãøn âäüng cuía hãû (S) trong hãû
quy chiãúu(R), cáön phaíi biãút 3n thäng säú (våïi mäùi cháút âiãøm cáön biãút ba toüa âäü x, y, z cuía noï).
1 Caïc hãû toaû âäü vaì laì caïc hãû toüa âäü De scartes
(; ; ; )
xyx
Oe e e
GGG (; ; ; )
SSS
xyz
Ce e e
GGG
12
Baìi giaíng Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
• Tuy nhiãn, âãø mä taí chuyãøn âäüng cuía váût ràõn (S) trong hãû quy chiãúu (R), chè cáön biãút nhiãöu
nháút laì 6 thäng säú, nhàòm mä taí chuyãøn âäüng cuía hãû quy chiãúu (RS) gàõn liãön våïi váût ràõn âäúi våïi
hãû quy chiãúu (R):
+ Ba thäng säú âãø xaïc âënh vë trê cuía gäúc cuía hãû quy chiãúu (RS) âäúi våïi hãû quy chiãúu (R) : ba
toüa âäü xOS, yOS, zOS cuía âiãøm OS trong hãû (R)
S
O
+ Ba thäng säú (ba goïc) âãø xaïc âënh phæång chiãöu cuía vectå âån vë S
x
e
G
cuía hãû (RS) âäúi våïi hãû (R):
α, β, γ
• Trong træåìng håüp chuyãøn âäüng cuía váût ràõn âæåüc dáùn hæåïng båíi mäüt säú raìng buäüc, säú thäng säú
cáön thiãút âãø mä taí chuyãøn âäüng cuía váût ràõn coï thãø < 6. Vê duû, vaình troìn chuyãøn âäüng trong màût
phàóng thàóng âæïng vaì luän tiãúp xuïc våïi màût âáút nàòm ngang chè cáön hai thäng säú âãø mä taí
chuyãøn âäüng cuía váût ràõn trong hãû quy chiãúu (R) (Hçnh 2):
⇒
+ Hoaình âäü x cuía tám C cuía vaình troìn trong hãû (R)
+ Goïc θ xaïc âënh phæång chiãöu cuía veïctå âån vë S
x
e
G
cuía hãû (RS) trong (R).
§2. Træåìng váûn täúc :
1) Quan hãû váûn täúc vaì gia täúc :
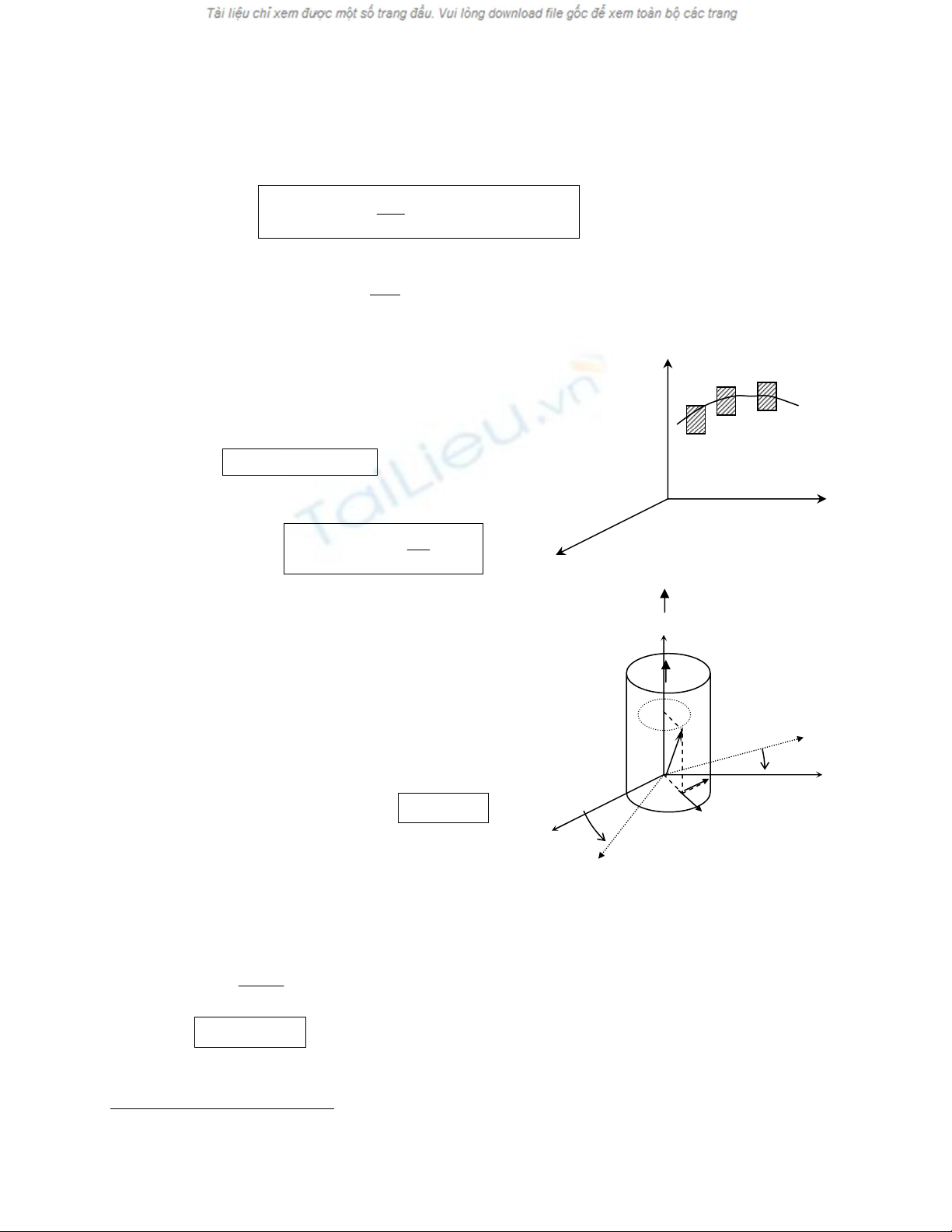
Xeït mäüt váût ràõn (S) chuyãøn âäüng trong hãû quy chiãúu
(R). Goüi (RS) laì hãû quy chiãúu gàõn liãön våïi váût ràõn (S)
vaì coï gäúc P, våïi P laì mäüt âiãøm cäú âënh trãn (S).
@ Goüi laì váûn täúc cuía âiãøm M thuäüc váût ràõn
(S) trong hãû quy chiãúu (R). AÏp duûng âënh lyï håüp váûn
täúc :
/
()
R
vM
K
//
() () ()
S
Re R
vM v M vM=+
KKK
våïi : : váûn täúc theo cuía âiãøm M. ()
e
vM
K
: váûn täúc cuía âiãøm M trong hãû quy
chiãúu (RS) (Âiãøm M cäú âënh trong hãû quy chiãúu (RS) :
/
()
S
R
vM
K
/
() 0
S
R
vM
=
K
)
Hçnh 4 y
O
z
P ° M
()S
(R)
()
S
zS
R
xS
yS
x
Goüi laì veïctå quay tæïc thåìi cuía váût ràõn (S) trong hãû quy chiãúu (R) (veïctå quay cuía hãû quy
chiãúu (RS) âäúi våïi hãû quy chiãúu (R))
/
S
RR
Ω
K
⇒ ///
() () () S
Re R RR
vM v M vP PM==+Ω×
J
JJJK
K
KKK
Viãút goün laûi, ta coï : () ()vM vP PM=+Ω×
J
JJJK
K
KK (1)
Nhæ váûy, khi biãút váûn täúc cuía mäüt âiãøm P vaì vectå quay tæïc thåìi
Ω
K
cuía váût ràõn (S) ⇒ coï thãø xaïc
âënh váûn täúc cuía mäüt âiãøm M báút kyì thuäüc váût ràõn (S) theo biãøu thæïc (1).
@ Tæång tæû, goüi laì gia täúc cuía âiãøm M thuäüc váût ràõn (S) trong hãû quy chiãúu (R). AÏp
duûng âënh lyï håüp gia täúc :
/
()
R
aM
G
//
() () () ()
S
R
eC
aM a M a M aM=+ +
GGGG
R
våïi : laì gia täúc theo cuía âiãøm M : ()
e
aM
G
/
//
() () ( )
S
SS
RR
e R RR RR
d
a M a P PM PM
dt
Ω
= + × +Ω×Ω×
GJJJJGJGJJJ
G
G
GG
laì gia täúc Coriolis :
()
C
aM
G
13
Baìi giaíng Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
do
//
()2. () 0
S
CRRR
s
aM vM=Ω × =
G
GG
/
() 0
Rs
vM
=
G
: gia täúc cuía âiãøm M trong hãû quy chiãúu (RS) (Âiãøm M cäú âënh trong hãû quy
chiãúu (RS) : )
/
()
S
R
aM
G
/
() 0
S
R
aM =
G
Viãút goün laûi, ta coï : () () ( )
d
aM aP PM PM
dt
Ω
= + × +Ω× Ω×
G
J
JJJGJGJJJ
G
G
GG (2)
Nhæ váûy, khi biãút gia täúc cuía mäüt âiãøm P, vectå quay tæïc thåìi
Ω
K
(coìn goüi laì vectå váûn täúc goïc tæïc
thåìi) vaì vectå gia täúc goïc tæïc thåìi d
dt
Ω
G
cuía váût ràõn (S) trong hãû quy chiãúu (R) ⇒ coï thãø xaïc âënh
gia täúc cuía mäüt âiãøm M báút kyì thuäüc váût ràõn (S) theo biãøu
thæïc (2).
Hçnh 5 y
z
(R)
()S
O
2) Caïc træåìng håüp âån giaín :
a) Váût ràõn (S) chuyãøn âäüng tënh tiãún :
Nãúu váût ràõn chuyãøn âäüng tënh tiãún trong (R)⇒ S0
Ω
=
K
⇒ () () ()vM vP vt==
KKK
Váûn täúc cuía moüi âiãøm M trãn váût ràõn taûi thåìi âiãøm t cho træåïc
âãöu bàòng nhau.
() () (
dv
aM aP at
dt
===
Tæång tæû cho gia täúc : )
K
GKK
x
O
z = zS
y
()R
Hçnh 6
xS
yS
M
° ()
S
R
Ω
G
z
e
G
z
θ
r
e
G
e
θ
G
θ
r
H
x
b) Váût ràõn (S) quay xung quanh mäüt truûc Oz cäú âënh
trong (R):
Xeït váût ràõn (S) quay xung quanh truûc Oz cäú âënh trong
hãû quy chiãúu (;; ; )
xyz
R
Oe e e
GGG. Gàõn cæïng våïi váût ràõn mäüt
hãû quy chiãúu (; , , )
SSSS
R
Ox y z nhæ hçnh 6 våïi Oz = OzS.
Goüi θ laì goïc quay cuía váût ràõn (S) quanh truûc Oz (goïc
quay cuía hãû quy chiãúu (RS) xung quanh truûc Oz cuía hãû
quy chiãúu (R)).
Veïctå quay cuía váût ràõn (S) trong (R): ().z
te
θ
Ω=
J
JK
K
Mäùi âiãøm M cuía váût ràõn vaûch nãn mäüt quyî âaûo hçnh troìn,
coï truûc laì Oz. Trong hãû toüa âäü truû, vë trê cuía M âæåüc xaïc
âënh bàòng :
JJJJ ..
r
OM re ze=+
z
GGG
(r vaì z khäng phuû thuäüc vaìo t)
@ Váûn täúc cuía âiãøm M trong (R) :
/
() ()
R
dOM
v M v O OM OM HM
dt
⎛⎞
==+Ω×=Ω×=Ω×
⎜⎟
⎝⎠
JJJJG
J
JJJK JJJJK JJJJK
K
KK
G
K(2)
⇒ () ..vM r e
θ
θ
=JJK
K
Vectå vM vuäng goïc våïi HM vaì hæåïng theo chiãöu chuyãøn âäüng cuía (S) trong hãû quy chiãúu R.
()
K
2 O vaì M laì hai âiãøm thuäüc váût ràõn nãn : () ()vM vO OM=+Ω×
J
JJJK
K
G
K; Ο cäú âënh trong R nãn
() 0vO =
G
14
Baìi giaíng Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
@ Gia täúc cuía âiãøm M trong (R) :
//
/
(( )) (.. )
() .. ..
RR
R
dvM dr e de
aM r r e
dt dt dt
θθ
θ
θ
θ
θ
⎛⎞
⎛⎞ ⎛⎞
===+
⎜⎟
⎜⎟ ⎜⎟
⎝⎠ ⎝⎠
⎝⎠
G
G
K
J
JK
G
våïi :
//
S
zr
RR
de de eeee
dt dt
θθ θθ θ
e
θ
θ
⎛⎞⎛⎞
= +Ω×=Ω×= ×=−
⎜⎟⎜⎟
⎝⎠⎝⎠
GG
GG
GGGG
G
(3)
⇒ 2
/
(( ))
() .. ..
r
R
dvM
aM r e r e
dt
θ
θ
θ
⎛⎞
==−+
⎜⎟
⎝⎠
K
J
KJK
G
J
@ Ghi chuï : Gia täúc cuía âiãøm M coï thãø phán thaình hai thaình pháön : Thaình pháön
hæåïng tæì M vãö H (goüi laì gia täúc hæåïng tám) vaì thaình pháön
()aM
G
2
() ..
n
aM r e
θ
=− JK
Gr() ..
t
aM r e
θ
θ
=
J
JK
G
vuäng goïc våïi HM (gia täúc tiãúp tuyãún).
3) Váût ràõn quay xung quanh truûc coï phæång khäng âäøi trong (R):
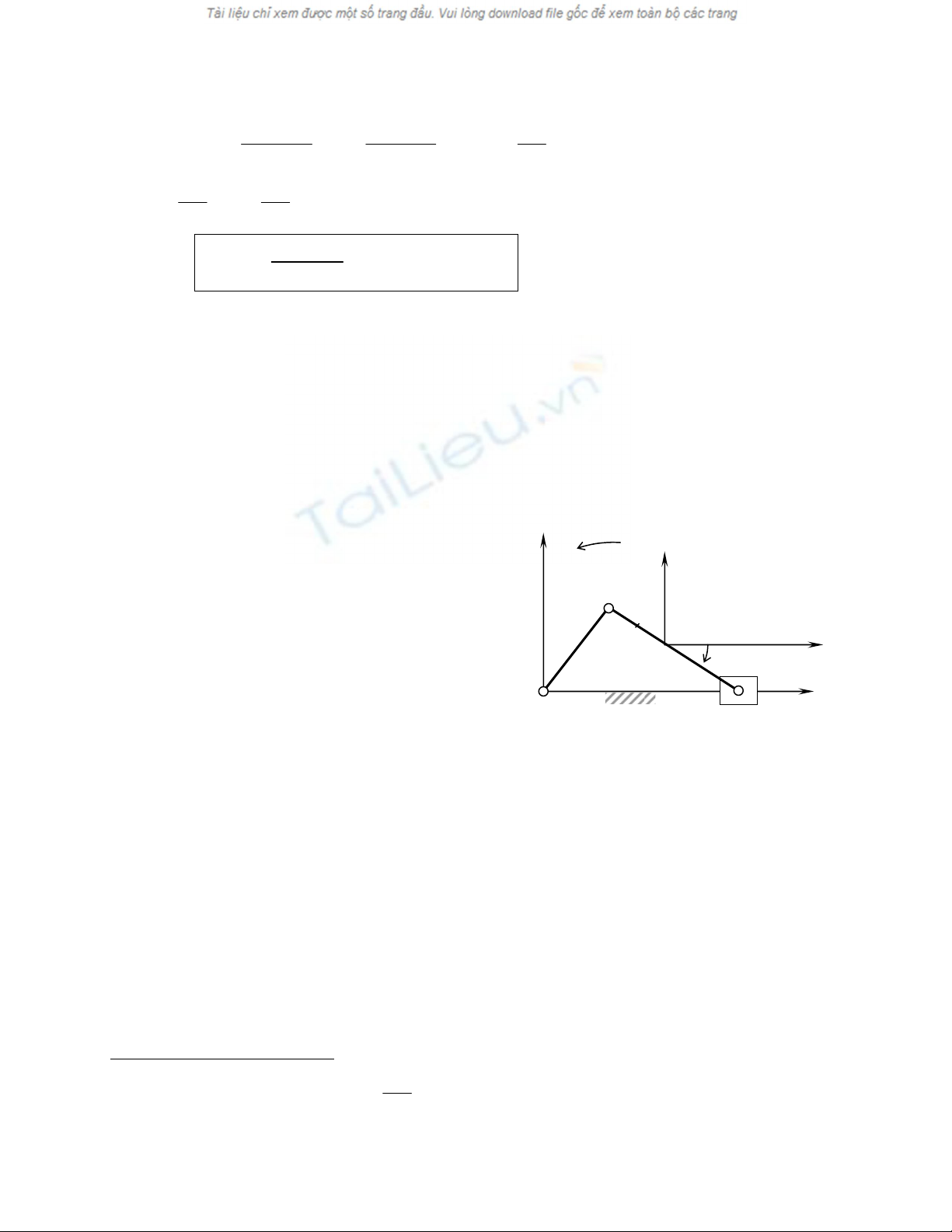
a) Vê duû 1 : Chuyãøn âäüng cuía thanh truyãön :
Xeït cå cáúu tay quay- con træåüt nhæ hçnh 7î, duìng âãø biãún chuyãøn âäüng quay cuía kháu OA thaình
chuyãøn âäüng tënh tiãún cuía con træåüt B vaì ngæåüc laûi. Haîy nghiãn cæïu chuyãøn âäüng cuía thanh
truyãön AB coï khäúi tám laì G.
Âãø nghiãn cæïu chuyãøn âäüng cuía thanh truyãön AB,
ta xeït thãm hãû quy chiãúu khäúi tám *( ; , , )
xyz
R
Ge e e
G
GG
tæång æïng våïi hãû quy chiãúu (R).
()R
y
x
A
OB
MG
x
y
θ
(*)R
⊕
z
:
@ Trong hãû quy chiãúu khäúi tám (R*), thanh truyãön
AB quay xung quanh truûc Gz cäú âënh. Goüi M laì
mäüt âiãøm báút kyì cuía thanh truyãön AB, ta coï :
JJJJ
()* ()* *vM vG GM=+Ω×
K
K
KK
**
K
våïi : vaì laì váûn täúc cuía M vaì G
trong hãû quy chiãúu khäúi tám (R*), laì
()vM
K()vG
K
*
Ω
K
Hçnh 7
vectå quay tæïc thåìi cuía thanh truyãön AB
JJ
K
trong hãû (R*) : *().
z
te
θ
Ω=
Do khäúi tám G cäú âënh trong hãû (R*) ⇒()* 0vG
=
K
⇒()* *vM GM=Ω ×
J
JJJK
K
K
Sæí duûng âënh lyï håüp váûn täúc, trong hãû quy chiãúu (R), ta coï :
() () ()*
e
vM v M vM=+
KK K
Hãû quy chiãúu khäúi tám (R*) chuyãøn âäüng tënh tiãún âäúi våïi hãû quy chiãúu (R)
⇒ () ()
e
vM vG=
KK
⇒ () () *vM vG GM=+Ω×
J
JJJK
K
KK (1)
@ Màûc khaïc, goüi Ω laì vectå quay tæïc thåìi cuía thanh truyãön AB trong hãû (R), ta coï :
K
() ()vM vG GM=+Ω×
J
JJJK
K
KK (2)
3 Chuï yï ràòng trong RS, e
θ
G khäng âäøi nãn
/
0
S
R
de
dt
θ
⎛⎞
=
⎜⎟
⎝⎠
G
15
Baìi giaíng Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
Tæì (1) vaì (2), suy ra : *(
z
te
θ
Ω=Ω= ).
J
JK
KK
Veïctå quay tæïc thåìi cuía váût ràõn laì nhæ nhau trong hai hãû quy chiãúu (R) vaì (R*). Måí räüng ra, veïctå quay
tæïc thåìi cuía váût ràõn laì nhæ nhau trong caïc hãû quy chiãúu chuyãøn âäüng tënh tiãún tæång âäúi âäúi våïi nhau.
@ Ghi chuï: Chuyãøn âäüng cuía thanh truyãön AB trong hãû quy chiãúu (R) coï thãø xem nhæ håüp cuía
hai chuyãøn âäüng:
• Chuyãøn âäüng tënh tiãún cuìng våïi khäúi tám G trong hãû quy chiãúu (R).
• Chuyãøn âäüng quay xung quanh mäüt truûc Gz âi qua khäúi tám G trong hãû quy chiãúu khäúi tám
(R*) (Truûc Gz cäú âënh trong hãû quy chiãúu khäúi tám (R*)).
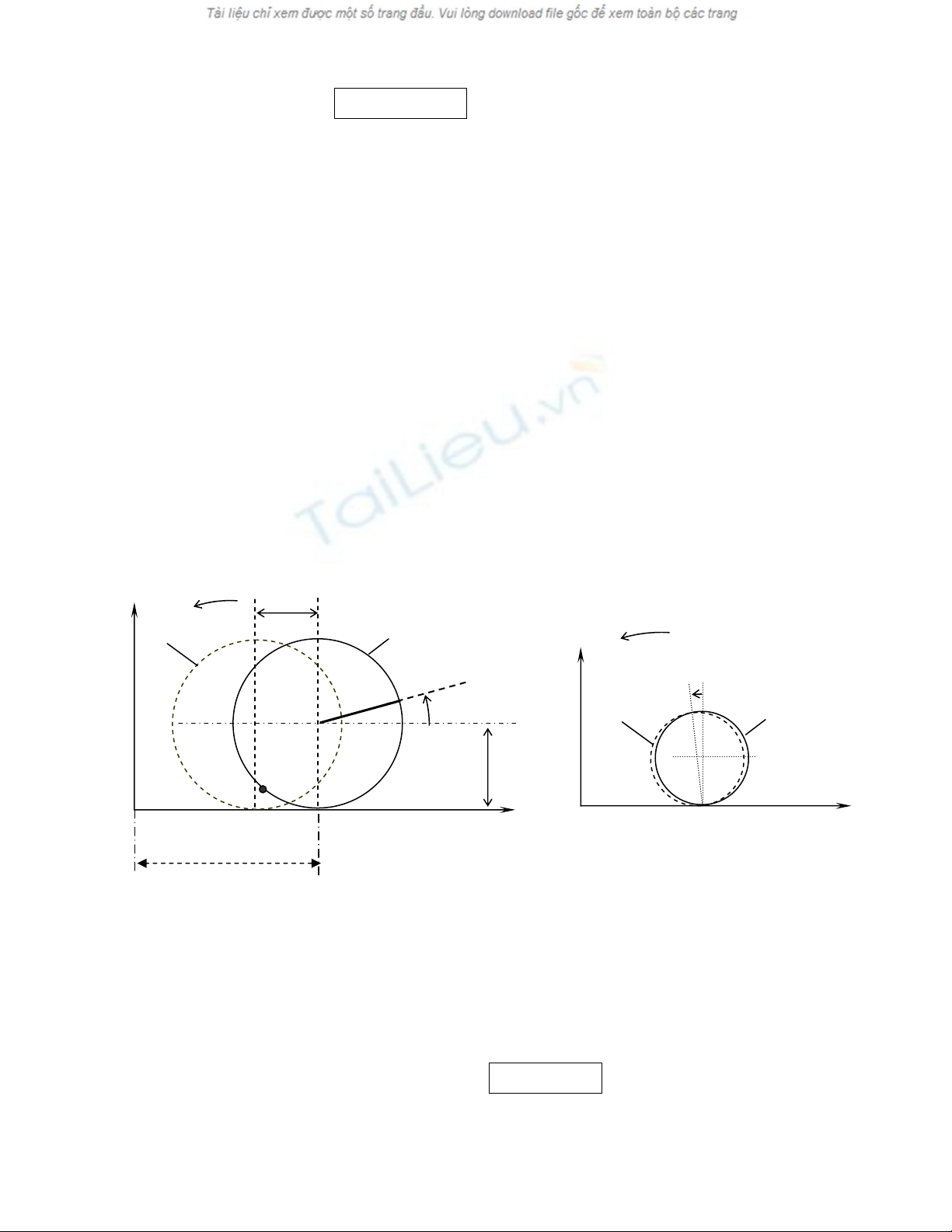
b) Vê duû 2 : Chuyãøn âäüng cuía mäüt baïnh xe :
@ Xeït mäüt baïnh xe, coi nhæ mäüt âéa troìn, baïn kênh b, tám C, chuyãøn âäüng trong màût phàóng thàóng
âæïng trãn màût âáút nàòm ngang cäú âënh trong hãû quy chiãúu (R) (Hçnh 8).
Goüi I laì âiãøm tiãúp xuïc cuía baïnh xe vaì màût âáút taûi thåìi âiãøm t. Taûi chäù tiãúp xuïc I vaìo thåìi âiãøm t,
cáön phán biãût ba âiãøm khaïc nhau:
• Âiãøm IS cuía màût âáút, cäú âënh trong (R).
• Âiãøm IR cuía baïnh xe. Do baïnh xe làn ⇒ taûi mäüt thåìi âiãøm sau âoï IR khäng coìn nàòm trãn màût
âáút næîa.
• Âiãøm hçnh hoüc I xaïc âënh vë trê tiãúp xuïc.
()R
y
O
C
z
I
Hçnh 9
C’
⊕
.dtΩ
taûi t
t
aûi t + δ
t
:
()∆
:Ω
G
y
O
z x
(R)
x
bb
I = IR = IS
Hçnh 8
JS = J
C
C’
∆x
:
x
θ
taûi t
taûi t + ∆
t
JR
:z
= e
θ
Ω
G
G
⊕
M (R*)
y
x
Taûi thåìi âiãøm t, ba âiãøm IS, IR vaì I coï váûn täúc khaïc nhau trong (R) :
()0
S
vI =
K
() ( )vI vC=
KK
, båíi vç I vaì C luän luän nàòm trãn cuìng mäüt âæåìng thàóng âæïng.
våïi : () ()
R
vI vC CI=+Ω×
JJK
K
KK
Ω
K
laì veïctå quay cuía baïnh xe trong (R).
Váûn täúc âæåüc goüi laì váûn täúc træåüt cuía baïnh xe trãn màût âáút (nhåï ràòng màût âáút laì cäú
âënh trong R). Ta tháúy
()
R
vI v=
K
g
K
g
v
Knàòm theo phæång tiãúp tuyãún chung taûi I giæîa baïnh xe vaì màût dáút.
@ Baïnh xe âæåüc goüi laì làn khäng træåüt nãúu nhæ : ()0
gR
vvI
=
=
K
K.
16