
316
BỒI DƯỠNG TƯ DUY HÀM CHO SINH VIÊN NGÀNH KINH TẾ
THÔNG QUA DẠY HỌC ỨNG DỤNG MÔ HÌNH HÀM SỐ
Nguyễn Chiến Thắng1*, Thái Thị Vân Anh2†
1 Khoa Toán - Ứng dụng, Trường Đại học Sài Gòn
2 Khoa Kinh tế - Trường Cao đẳng Kinh tế - Kế hoạch Đà Nẵng
TÓM TẮT
Nghiên cứu này nhằm hiểu được tư duy hàm của sinh viên kinh tế khi học
nội dung hàm số, với hai câu hỏi nghiên cứu chính: (1) Các quá trình tư duy hàm
mà sinh viên kinh tế phát triển là gì? (2) Sinh viên gặp những khó khăn nào khi
tìm hiểu về các hàm trong phân tích kinh tế? Mức độ tư duy hàm của sinh viên
được khảo sát, đánh giá trên các khía cạnh: nhận diện mối quan hệ, phân tích sự
tương ứng, xây dựng mô hình, khái quát hóa và ứng dụng thực tiễn. Ngoài ra,
phương pháp phỏng vấn sinh viên được triển khai để thu thập phản hồi về chương
trình giảng dạy và ảnh hưởng của nó đến quá trình tư duy hàm của sinh viên. Kết
quả cho thấy khả năng tư duy hàm của sinh viên khác nhau. Tuy nhiên, nhiều
sinh viên vẫn gặp khó khăn đáng kể trong phát triển tư duy hàm, đặc biệt là trong
khả năng mô hình hóa, khái quát hóa và ứng dụng thực tiễn.
Từ khóa: Tư duy hàm; hàm số; kinh tế; sinh viên; bồi dưỡng
1. Giới thiệu
Phát triển kỹ năng suy luận của sinh viên là mục tiêu cơ bản của giáo dục
đại học, đặc biệt trong các lĩnh vực dựa nhiều vào tư duy phân tích, chẳng hạn
như kinh tế
1
. Những kỹ năng này giúp sinh viên tiếp thu và diễn đạt kiến thức
thông qua các quá trình như suy đoán, khái quát hóa, điều tra, hình thành và đánh
giá các lập luận về các khái niệm phức tạp. Ở bậc đại học, khả năng suy luận của
sinh viên phát triển từ cụ thể đến trừu tượng, trong đó việc nghiên cứu các hàm
số đóng vai trò then chốt
2
. Nội dung các môn học về hàm số rất quan trọng để
mô hình hóa và phân tích các hiện tượng kinh tế khác nhau. Việc hiểu các hàm
này đòi hỏi sinh viên phải giải thích và vận dụng các cách biểu diễn khác nhau,
bao gồm các dạng số, đồ thị và đại số. Các kỹ năng này rất cần thiết để rèn luyện
tư duy hàm, bao gồm việc nhận biết và khái quát hóa các mô hình cũng như mối
quan hệ giữa các biến số. Tư duy hàm không chỉ là một thành phần chính của lý
1
Arslan, R., Gulveren, H., Aydin, E. (2014), “Research on critical thinking tendencies and factors that affect
critical thinking of higher education students”, International Journal of Business and Management, 9(5).
2
Oehrtman, M., Carlson, M., Thompson, P. W. (2008), “Foundational reasoning abilities that promote
coherence in students’ function understanding”, Making the connection: Research and teaching in
undergraduate mathematics education, 27, p. 42.

317
luận toán học mà còn là một công cụ quan trọng để phân tích kinh tế và ra quyết
định. Việc hiểu và vận dụng các hàm số đặt ra những thách thức đáng kể. Sinh
viên thường gặp khó khăn trong việc kết nối các biểu diễn hàm khác nhau, diễn
giải đồ thị một cách chính xác, thao tác ký hiệu và hiểu thuật ngữ chuyên ngành
liên quan đến các hàm này. Điều đó có thể cản trở khả năng áp dụng lý thuyết
vào các vấn đề kinh tế thực tế một cách hiệu quả.
Bài viết đề xuất lồng ghép giảng dạy các hàm số trong phân tích kinh tế
vào chương trình học, nhằm cải thiện kỹ năng phân tích, dự báo và hiểu biết của
sinh viên về các khái niệm kinh tế cốt lõi. Nghiên cứu tập trung xác định các quá
trình tư duy hàm và những khó khăn sinh viên gặp phải để phát triển chiến lược
giáo dục hiệu quả hơn. Nghiên cứu này dự định trả lời các câu hỏi nghiên cứu
sau:
(1) Các quá trình tư duy hàm được sinh viên kinh tế phát triển trong quá
trình học nội dung hàm số là gì?
(2) Khó khăn gặp phải khi tìm hiểu về các hàm trong phân tích kinh tế?
2. Phương pháp nghiên cứu
Nghiên cứu đã khảo sát 46 sinh viên ngành kinh tế ở các trường đại học
chuyên ngành kinh tế ở Việt Nam thông qua Google Form. Thời gian thực hiện
đầu tháng 6/2024, lúc này sinh viên đã học xong nội dung môn Toán. Bài kiểm
tra được sử dụng để đánh giá mức độ tư duy hàm của sinh viên, gồm 20 câu hỏi
ở các mức độ về tư duy hàm. Ngoài ra phương pháp phỏng vấn được dùng để
thu thập phản hồi về chương trình giảng dạy và cách nó ảnh hưởng đến khả năng
tư duy hàm của sinh viên.
3. Kết quả và thảo luận
3.1. Tư duy hàm
Theo Smith
1
, tư duy hàm là khả năng tập trung vào mối quan hệ giữa
hai/nhiều đại lượng/biến thay đổi trong toán học. Theo Nguyễn Bá Kim (1994),
tư duy hàm thể hiện được sự nhận thức được tiến trình những tương ứng riêng
và chung giữa các đối tượng toán học hay những tính chất của chúng, kể cả kỹ
năng vận dụng chúng. Theo quan điểm của tác giả, tư duy hàm là hoạt động trí
tuệ được sử dụng để nghiên cứu các mối quan hệ và sự tương ứng giữa hai hoặc
nhiều đại lượng thay đổi và dẫn đến sự khái quát hóa.
1
Smith, E. (2008), “Representational thinking as a framework for introducing functions in the elementary
curriculum”, In Algebra in the early grades (Routledge, pp. 133-160), In J. J. Kaput, D. W. Carraher &
M. L. Blanton (Eds.).

318
Trong tư duy hàm, hàm số được sử dụng làm cơ sở cho hệ thống biểu diễn
trong các trường hợp khác nhau
12
. Tư duy hàm liên quan đến cốt lõi của tư duy
đại số: sự khái quát hóa và biểu tượng hóa
34
. Khái quát hóa là quá trình nhận
dạng mẫu từ các đối tượng đã xác định
5
, trong khi ký hiệu hóa là quá trình sử
dụng hệ thống ký hiệu để thể hiện khái quát hóa5. Trong giai đoạn chuyển tiếp
từ trung học cơ sở lên trung học phổ thông, kiến thức của học sinh về hàm số là
điều kiện tiên quyết để tiếp tục học tập. Ở giai đoạn này, các biến số tiến từ rời
rạc sang liên tục, yêu cầu tăng khả năng trừu tượng, điều mà một số tác giả cho
rằng có ảnh hưởng đến việc xác định các đặc điểm tích hợp tư duy hàm. Tư duy
hàm là trung tâm khi liên quan đến hai hoặc nhiều đại lượng biến đổi, ví dụ như
sự phụ thuộc giữa tốc độ, khoảng cách và thời gian, hoặc khi mô hình hóa sự lây
lan của virus. Nó cũng có liên quan đến việc học các môn khác và hiểu biết các
tình huống hàng ngày. Pittalis và cs.
6
mô tả tư duy hàm là quá trình xây dựng,
mô tả và lập luận với và về các hàm số. Theo Lichti và Roth
7
, tư duy hàm bao
gồm ba đặc điểm cơ bản: ánh xạ, sự cùng biến thiên và hàm số như một đối
tượng.
Việc bồi dưỡng tư duy hàm cho sinh viên kinh tế thông qua việc giảng
dạy các hàm số thông dụng trong phân tích kinh tế là rất quan trọng. Trong kinh
tế học, hiểu các mối quan hệ hàm số như cung và cầu, chi phí và doanh thu, hoặc
tác động của lãi suất đối với đầu tư là rất cần thiết. Tư duy hàm giúp sinh viên
nắm bắt sự tương tác giữa các biến kinh tế khác nhau và áp dụng các khái niệm
này vào các kịch bản kinh tế thực tế. Bằng cách học cách ánh xạ các mối quan
hệ, hiểu sự cùng biến thiên và xem hàm số như các đối tượng toàn diện, sinh viên
có thể phát triển sự hiểu biết sâu sắc hơn về các lý thuyết và mô hình kinh tế
89
.
Việc tích hợp các bài tập sử dụng các biểu diễn khác nhau của hàm số,
như đồ thị, bảng và công thức đại số được sử dụng thường xuyên trong giáo dục
1
Oehrtman, M., Carlson, M., Thompson, P. W. (2008), Tlđd.
2
Günster, S. M., Weigand, H. G. (2020), “Designing digital technology tasks for the development of
functional thinking”, ZDM, 52(7), pp. 1259-1274.
3
Kaput, J. (2008), “What is Algebra? What is Algebraic reasoning?”, In Algebra in the early grades
(Routledge, 5-18). In J. J. Kaput, D. W. Carraher, & M. L. Blanton (Eds.).
4
Smith, E. (2008), Tlđd.
5
Maudy, S. Y., Didi, S., Endang, M. (2018), “Student’ algebraic thinking level”, International Journal
of Information and Education Technology, 8(9), pp. 672-676.
6
Pittalis, M., Pitta-Pantazi, D., Christou, C. (2020), “Young students’ functional thinking modes: the
relation between recursive patterning, covariational thinking, and correspondence relations”, Journal for
research in mathematics education, 51, pp. 631-674.
7
Lichti, M., Roth, J. (2018), “How to foster functional thinking in learning environments using computer-
based simulations or real materials”, Journal for STEM education research, 1, pp. 148-172.
8
Lê Đình Thúy (2010), Toán cao cấp cho các nhà kinh tế, Nxb Thống kê, Hà Nội.
9
Lê Văn Hốt (2000), Toán cao cấp, Nxb Đại học Kinh tế TP. Hồ Chí Minh.

319
kinh tế. Cách tiếp cận này giúp sinh viên hình dung và diễn giải các mối quan hệ
kinh tế, khuyến khích khả năng tổng quát hóa từ các trường hợp cụ thể đến các
nguyên lý kinh tế rộng hơn. Để bồi dưỡng những kỹ năng này, điều cần thiết là
sử dụng nhiều dạng biểu diễn và các bài tập thách thức sinh viên nhận diện và
trình bày các mối quan hệ giữa các biến số. Từ đó xây dựng sự hiểu biết vững
chắc về các hàm kinh tế và cải thiện khả năng giải quyết vấn đề. Bằng cách tập
trung vào tư duy hàm từ giai đoạn đầu, các nhà giáo dục có thể chuẩn bị cho sinh
viên phân tích kinh tế phức tạp hơn và trang bị các công cụ cần thiết cho sinh
viên.
Theo tác giả, các biểu hiện của tư duy hàm của sinh viên ngành kinh tế
bao gồm:
- Nhận diện mối quan hệ: Xác định cách các đại lượng thay đổi liên quan
đến nhau, chẳng hạn như sự phụ thuộc của lượng cầu vào giá cả trong kinh tế.
- Phân tích sự tương ứng: Xác định các tương ứng giữa các giá trị của các
đại lượng, ví dụ như việc lập bảng hoặc biểu đồ để mô tả mối quan hệ giữa chúng.
- Xây dựng mô hình: Sử dụng hàm số để mô tả các mối quan hệ này, chẳng
hạn như các hàm tuyến tính, hàm bậc hai, hay hàm mũ.
- Khái quát hóa: Từ các mô hình cụ thể, rút ra các nguyên lý hoặc quy
luật tổng quát có thể áp dụng cho các tình huống tương tự khác. Ví dụ, nhận biết
rằng hàm cầu thường có dạng giảm dần khi giá tăng.
- Ứng dụng thực tiễn: Sử dụng các khái quát hóa và mô hình để giải quyết
các vấn đề thực tiễn, đưa ra dự đoán hoặc đề xuất giải pháp dựa trên sự hiểu biết
về mối quan hệ giữa các đại lượng.
3.2. Các biểu hiện của tư duy hàm thông qua dạy học ứng dụng mô hình hàm số
Ví dụ 1. Giả sử hàm cầu cho sản phẩm giày dép có dạng tuyến tính: 𝑄𝑑=
𝑎.𝑃+𝑏, trong đó: 𝑄𝑑 là lượng cầu, 𝑃 là giá sản phẩm, 𝑎 và 𝑏 là các hệ số xác
định đặc trưng của hàm cầu. Giá của sản phẩm 100.000; 150.000; 200.000;
250.000 và lượng cầu tương ứng 200; 150; 100; 50. Hãy lập mô hình hàm cầu
và cho nhận xét từ mô hình trên.
Nhận diện mối quan hệ: Quan sát sự thay đổi của lượng cầu khi giá thay
đổi: Ví dụ, khi giá tăng từ 100.000 lên 150.000 VND, lượng cầu giảm từ 200
xuống 150. Điều này cho thấy mối quan hệ nghịch giữa giá và lượng cầu.
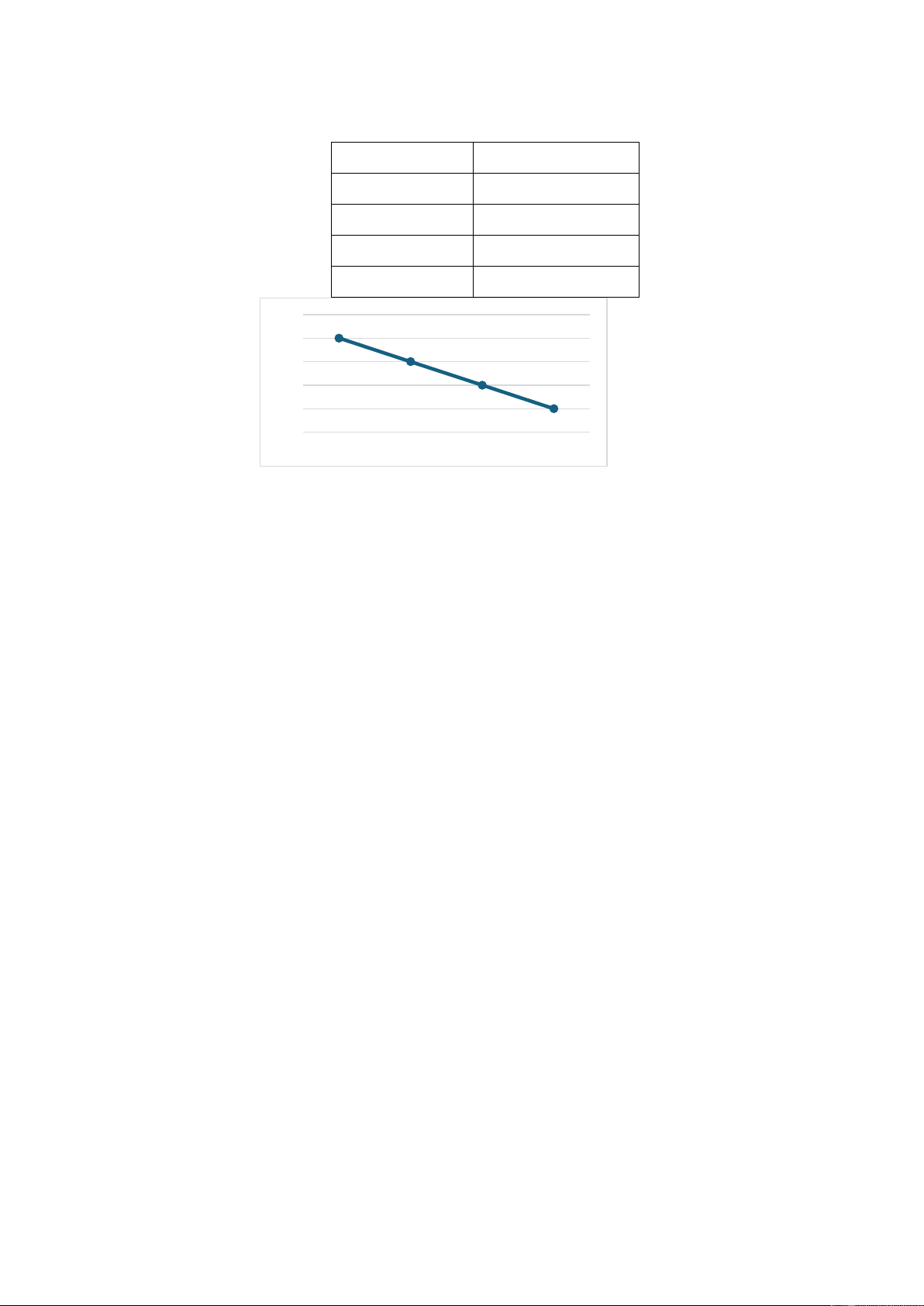
Phân tích sự tương ứng: Bảng 1 mô tả mối quan hệ giữa giá 𝑃 và lượng
cầu 𝑄𝑑.
320
Bảng 1. Mối quan hệ giữa giá và lượng cầu
𝑃
𝑄𝑑
100.000
200
150.000
150
200.000
100
250.000
50
Hình 1. Đồ thị mô phỏng sự tương ứng giữa giá và lượng cầu
Xây dựng mô hình: Sử dụng dữ liệu để ước lượng các hệ số trong hàm
cầu. Từ dữ liệu, có thể tìm được hệ số a và b bằng cách giải hệ phương trình:
{200=𝑎.100000+𝑏
150=𝑎.150000+𝑏.
Giải ra ta được 𝑎=−0,001;𝑏=300. Mô hình hàm cầu là:
𝑄𝑑=−0,001.𝑃+300.
Khái quát hóa: Từ mô hình cụ thể, rút ra nguyên lý: khi giá sản phẩm
tăng, lượng cầu giảm và ngược lại. Mối quan hệ này thường được biểu diễn bằng
đường cầu dốc xuống. Chẳng hạn, nhận biết rằng khi giá tăng thêm một đơn vị,
lượng cầu sẽ giảm đi một lượng tương ứng theo hệ số b.
Ứng dụng thực tiễn: Sử dụng mô hình và các nguyên lý khái quát hóa để
dự đoán lượng cầu trong các tình huống tương tự. Ví dụ, nếu giá sản phẩm là
180.000 đồng, dự đoán lượng cầu sẽ là: 𝑄𝑑=−0,001.180000+300=120.
Ví dụ trên giúp sinh viên hiểu rõ cách giá cả ảnh hưởng đến lượng cầu.
Bằng cách nhận diện mối quan hệ, phân tích sự tương ứng, xây dựng mô hình,
khái quát hóa và áp dụng thực tiễn, các nguyên lý kinh tế có thể được áp dụng
để dự đoán và giải quyết các vấn đề thực tế liên quan đến thị trường và hành vi
tiêu dùng.
Ví dụ 2. Một hãng sản xuất mỹ phẩm độc quyền dự định bán ra thị trường
hai loại sản phẩm chăm sóc da. Qua quá trình khảo sát nhu cầu thị trường và
ước lượng giá bán tương ứng, hãng sản xuất có được số liệu ở Bảng 2.
0
50
100
150
200
250
100 000 150 000 200 000 250 000


























