50
2.3. Những phương pháp giải bài toán QHTT
2.3.1.
2.3.1. Phương
Phương ph
phá
áp
pđ
đồ
ồth
thị
ị
2.3.2.
2.3.2. Phương
Phương ph
phá
áp
pđơn
đơnh
hì
ình
nh
a.
a. Xác định miềnchấpnhậnđược
b.
b. Tìm giá trịcủahàmmụctiêutrênmiềnchấpnhận
a.
a. Thuật toán đơnhìnhgiảibàitoándạng chuẩn
b.
b. Thuật toán đơnhìnhgiảibàitoánmởrộng
c.
c. Giảibằng máy tính
51
2.3.1. Phương pháp đồ thị
Trong các phương pháp giải bài toán qui hoạch tuyến tính,
phương pháp đồ thị(Phương pháp hình học) thường đượcsử
dụng. Phương pháp này có ưuđiểmlàtrực quan, dễhiểu. Tuy
nhiên, phương pháp này chỉdùng để giảinhững bài toán hai
biếnquyếtđịnh.
Vềcơbảnphương pháp này gồmhaibướcsau:
Xác định miềnphương án chấpnhậnđược;
Từđótìmphương án tốiưutrênmiềnchấtnhậnđó.
52
a. Xác định miềnchấpnhậnbằng đồ thị
Mỗitrụcthểhiệnmộtbiếnquyếtđịnh;
Mỗiràngbuộcvẽmộtđường thẳng để xác định miềnchấp
nhận:
Mỗiđường thẳng chỉcầnvẽ2 điểmvànối chúng với nhau;
Chọnmộtđiểmbấtkỳthoảmãn ràng buộc, miềnchứađiểmđó
sẽlà miềnchấpnhậnthỏamãnràngbuộcđang xét;
Giao tấtcảcác miềnchấpnhậncủa các ràng buộc hình thành
vùng chấpnhậncủa bài toán.
Bấtcứđiểmnàonằmtrênđường biên của vùng chấpnhậnhoặc
trong vùng chấpnhậnđượcgọilàđiểmphương án chấpnhậnđược
đốivới bài toán qui hoạch.
53
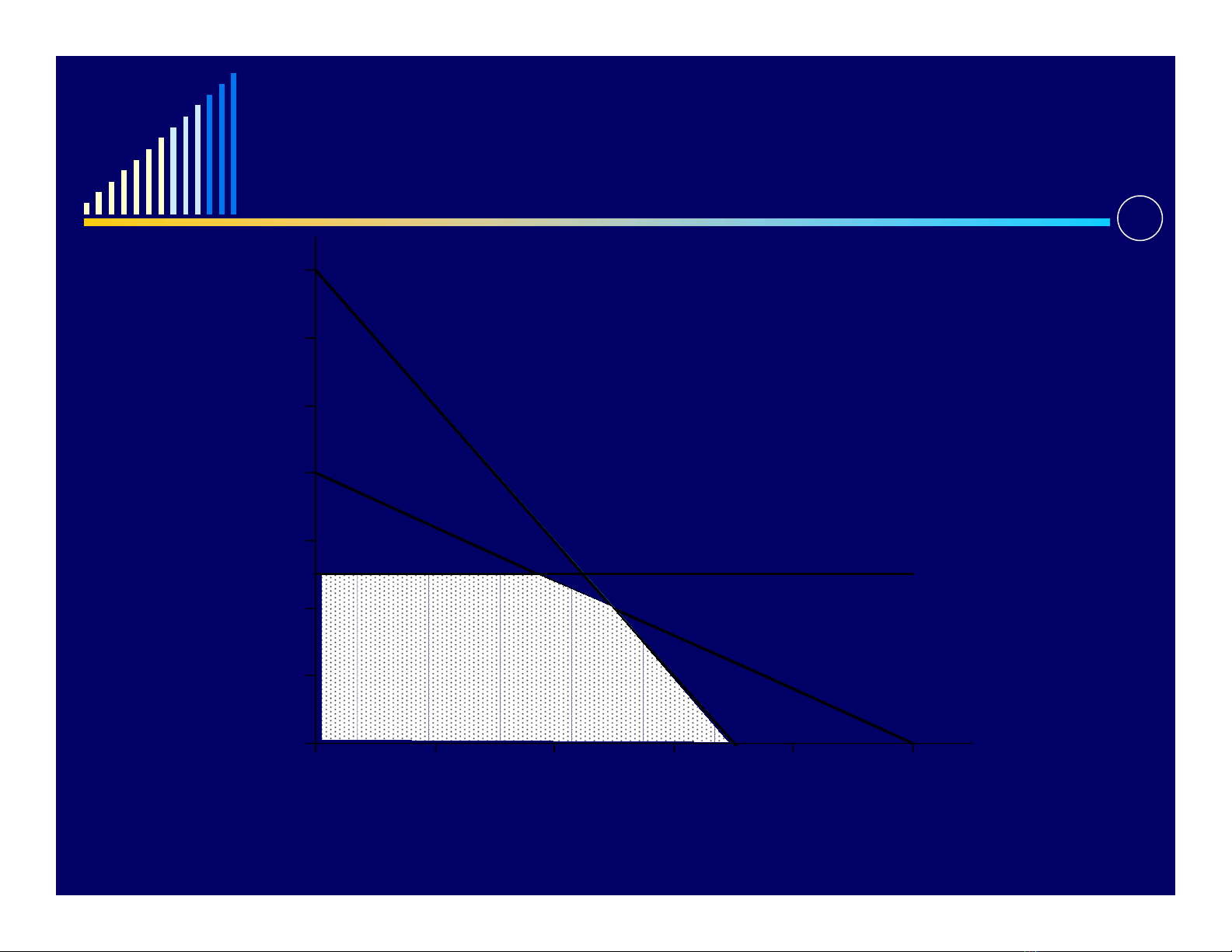
a. Tiếp
Nguyên liệu 2
Nguyên liệu 1
Nguyên liệu 3
0
10
20
30
40
50
60
70
0 1020304050
Số tấn chất phụ gia
Số tấn chất bazơ hoà tan
Vùng chấp nhận
54
b. Tìm giá trịcủahàmmụctiêutrênmiền
chấpnhận
0
10
20
30
40
50
60
70
0 1020304050
Số tấn chất phụ gia
Số tấn chất bazơ hoà tan
Phương án tối ưu
F=25
,
B=20