Một số cách xác định công thức tổng quát
của một số dạng dãy số cơ bản
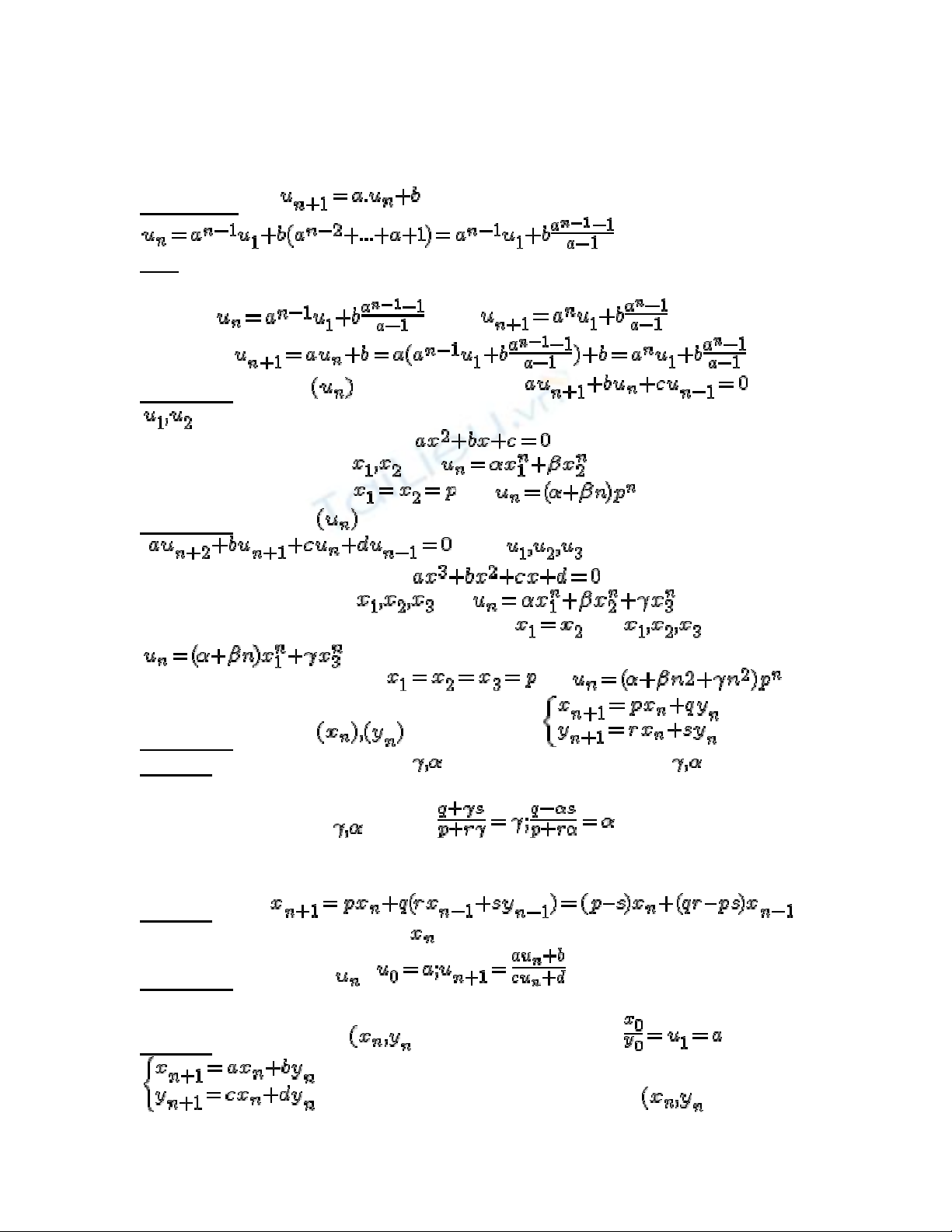
Kết quả 1: Dãy có số hạng tổng quát là
Cm: Ta chứng minh bằng phương pháp quy nạp
*n=1 ta thấy (1) đúng
*Giả sử ta cm
Thậy vậy: đpcm
Kết quả 2:Với dãy được xác định bởi : , biết
Ta xét phương trình đặc trưng: (*)
-Nếu (*) có hai nghiệm thì:
-Nếu (*) có nghiệm kép thì :
Kết quả 3: Với dãy được xác định bởi
: , biết
Ta xét phương trình đặc trưng: (**)
-Nếu (**) có ba nghiệm thì:
-Nếu (**) có 1 nghiệm đơn, 1 nghiệm kép thì: thì:
-Nếu (**) có nghiệm bội ba thì:
Kết quả 4: Với dãy được xác định:
Cách 1: Đưa vào tham số phụ . Nhân vào pt thứ hai với và cộng hai
pt vào ta được
Tiếp theo ta xác định sao cho .Nếu hai pt này có
nghiệm khi đó ta có
Từ đây chúng ta xác định được cttq của các dãy đã cho
Cách 2: ta có: ta
dễ dạng tìm được cttq của dãy theo kết quả 2
Kết quả 5:Với dãy số : với mọi n 1. Đối với dạng
này ta có hai cách làm như sau:
Cách 1: Xét hai dãy số được xác định như sau: ;
Theo kết quả 4 ta xác định được dãy và khi đó
dãy :
Cách 2:Ta đưa vào các tham số x,y như sau:
Tiếp theo ta xác định x,y sao cho:
. Khi đó ta có: . Đặt
. Ta được . theo kết quả 1 ta xác định
được dãy nên ta tìm được
Sau đây là các ví dụ:
Ví dụ 1: Cho dãy và .Tìm số hạng
tổng quát của dãy
Lời giải: Bài này chúng ta có thể giải theo các cách sau:
Cách 1: Xét pt đặc trưng: pt này có hai nghiệm
nên . Vì nên ta suy ra . Vậy
Cách 2: Đặt ta có nên ta có
suy ra lấy tổng hai vế ta có
Ví dụ 2: Cho dãy số xác định bởi:
a)Tìm công thức tổng quát của dãy
b)Chứng minh rằng nếu p là số nguyên tố thì chia hết cho p
Lời giải :
Xét pt đặc trưng: pt này có ba nghiệm
nên Theo gt nên ta có hệ
gồm ba pt sau:
giải hệ ba pt này ta có
nghiệm
Vậy
b)Ta có 1 1 (mod p)
Vì p là số nguyên tố nên theo định lí nhỏ Fecma ta có:
Suy ra đpcm
Ví dụ 3: Cho dãy
a) Tính
b) Tìm phần nguyên:
Lời giải:
Ta có:
Đặt . Ta có
Áp dụng kết quả 1 ta có:
a) Theo trên ta có:
b) Ta có:
Mặt khác:
Ví dụ 4:Cho hai dãy được xác định như sau:
. Tìm
công thức tổng quát của hai dãy
Lời giải:
Ta có: . ta chọn sao
cho:
Do đó ta có hệ:
Suy ra:
Ví dụ 5: Cho dãy với mọi
n>=2. Cmr
Lời giải: Để chứng minh bài toán ta chỉ cần chứng minh
có là được
Dãy số đã cho gần giống với dạng ở kết quả 2, nhưng vì có hệ số tự do 1975
nên ta chưa áp dụng được kết quả 2.Chúng ta có thể chuyển về dạng ở kết
quả 1 bằng cách đặt . Khi đó
, đến
đây ta chọn a,b sao cho 22a-8b=0, chọn a=4, b=11
Suy ra
Phương trình đặc trưng có hai nghiệm x=-1 và x=-5 nên
dựa vào ta xác định được
. Do đó suy ra
Do 1997 là số nguyên tố nên theo định lí nhỏ Féc ma ta có:
(vì (4;1997)=1) đpcm
Chú ý: Theo chứng minh ở trên ta có bài toán tổng quát hơn là :Cmr
với mọi số nguyên tố p
Ví dụ 6: Cho hai dãy được xác định như sau: và
. Tìm tất cả các số
nguyên tố p sao cho : không chia hết cho p
Lời giải:
Ta có:
Mặt khác: . Đặt
Đặt ta có: . Áp dụng kết quả 1 ta có được .
Thay vào (1) ta có:
*p=2 không thỏa mãn
*p=3 không chia hết cho 3, suy ra p=3 thỏa mãn
*p=5 thỏa mãn
*p 5 khi đó không thỏa
mãn
Vậy p=3,5 là những số cần tìm
Các bài tập
1) Cho dãy được xác định bởi . Xác định công thức
tổng quát của dãy ?
2) Cho dãy số . Cmr:
là số chính phương
3) Cho dãy
a) Xác định công thức tổng quát của dãy
b)Đặt . Tìm để dãy có giới hạn và tìm giới hạn đó
4)Cho hai dãy được xác định như sau:
. Cmr:
5) Cho dãy
a) Tìm số nguyên dương h bé nhất để: với mọi n
b) Cmr tồn tại ít nhất một số của dãy chia hết cho 1996