Lecturer: Date Approved by: Date
Oct. 16th,
2023
Oct. 16th,
2023
ThS. Phan Thị Khánh Vân
.....................................................................................................
UNIVERSITY OF TECHNOLOGY - VNUHCM
Faculty of Applied Science
Midterm Exam
Academic year 2023-2024 Semester 1
Exam date October 28th, 2023
Course title Linear Algebra Score
Course ID MT1007 Sheet code 3131
Duration 50 minutes Shift 12:00
Instructions to students:
- This is a closed book exam. Only your calculator is allowed. Total available score: 10.
- At the beginning of the working time, you MUST fill in your full name and student ID on this question
sheet. There are 20 questions on 4 pages.
- Do not round between steps. Round your final answers to 4 decimal places.
Student’s full name: ...................................... Invigilator 1: .......................
Student Id: ................... Group: ...... .......... Invigilator 2: .......................
1. (L.O.1,L.O.2) Given two matrices A∈M2×4and B∈M5×5.Let Xand Ysatisfy Y=AXB. Then,
the size of Xis:
A None of the others B X∈M4×5CX∈M4×2DX∈M3×5EX∈M5×4
2. (L.O.1,L.O.2) Find the rank of the matrix A=
1202
2−1−1−4
1 2 −4 1
1−134
.
A1B None of the others C 3D2E4
3. (L.O.1,L.O.2) Let Abe the matrix
1 1 1
1−4 3
3 2 2
with the determinant 7. Evaluate det(2A3).
A512 B None of the others C 2744 D1000 E1728
4. (L.O.1,L.O.2) In the vector space R3,let mbe a real number and
M={(1,−4,1),(2,−7,2),(1,2, m),(3,−11,3)}
be a vector set. Find msuch that Mis a spanning set of R3.
Am= 3 Bm=−2Cm= 1 D None of the others E m= 0
5. (L.O.1,L.O.2) In the vector space P2[x],let mbe a real number and
M={−4x2+ 2x+ 1, x2+ 2,2x+m}be a vector set. Find msuch that Mis linearly independent.
Am= 6 Bm= 9 Cm= 11 Dm= 8 E None of the others
6. (L.O.1,L.O.2) A circuit is given in the following figure.
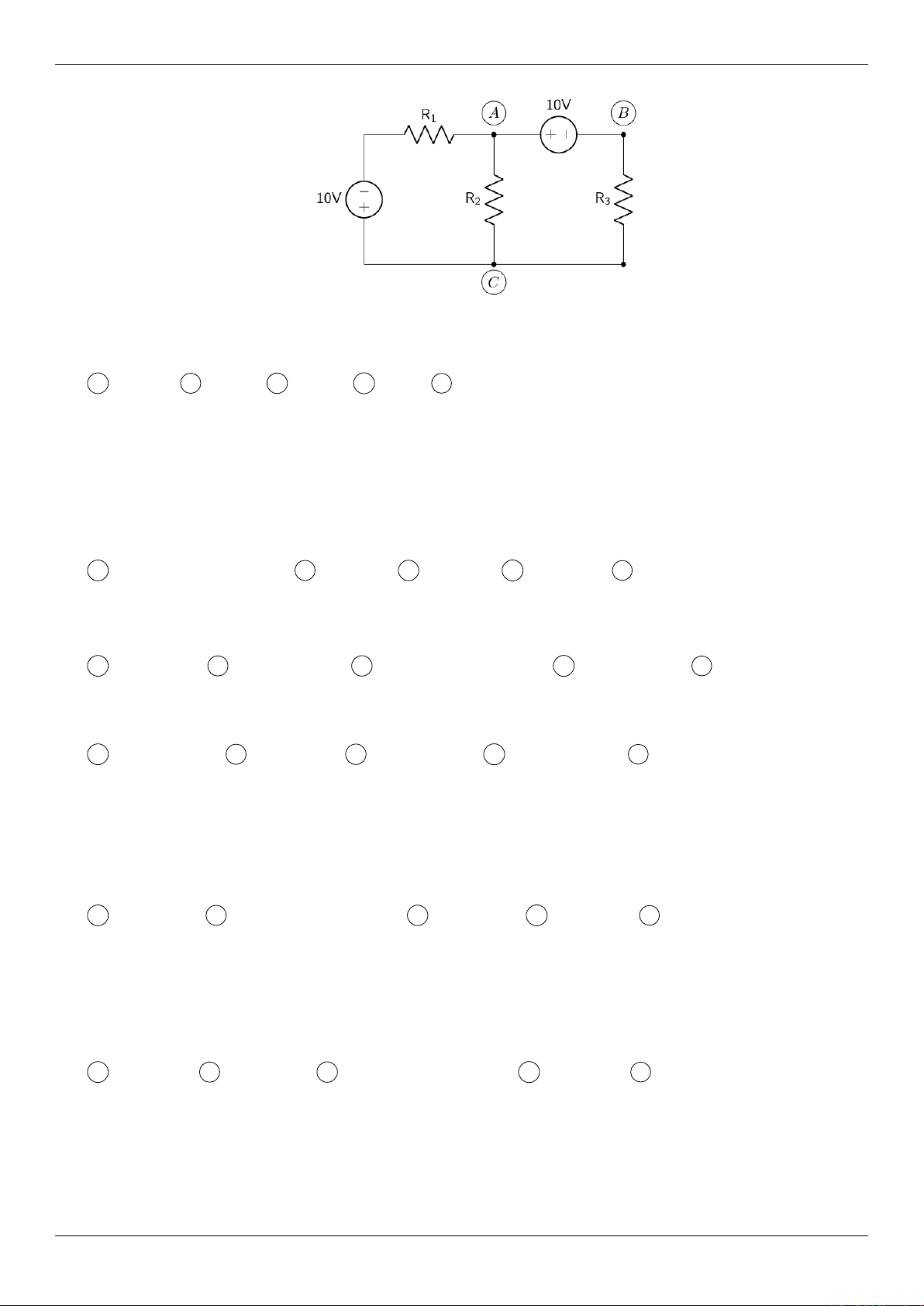
Midterm Exam
- MT1007 3131 - 12:00 Semester 1 - October 28th, 2023
Given that R1= 2Ω,R2= 5Ω,R3= 4Ω. Find the current which flows through R1(the result is
rounded to 2 decimal digits.).
A3.68 B3.67 C3.23 D4.0E None of the others
Questions 7 through 9
Let mbe a real number such that the system
x1+ 2x2−x3= 2
2x1+ 3x2+ (m−2)x3= 2
3x1+ 4x2+mx3= 2,
has infinitely many solutions.
7. (L.O.1,L.O.2) Find m.
A There is no such mBm= 5 Cm= 4 Dm= 3 E None of the others
8. (L.O.1,L.O.2) Let (x1, x2, x3)be a solution of the above system satisfying x1=x2.
Find x3.
Ax3=−1Bx3=−1/2C None of the others D x3=−3/7Ex3=−5
9. (L.O.1,L.O.2) In R3,let x= (x1, x2, x3)be a solution of the above system (a vector in R3), given
that xis a linear combination of M={(1,1,0),(1,3,2)}.Find x3.
Ax3=−3/7Bx3=−5Cx3=−5/6Dx3=−4/7E None of the others
Questions 10 through 11
In the vector space R3,given that E={(1,2,−4),(2,5,−3),(−4,−3, m)}
and F={(1,0,0),(1,1,0),(1,1,1)}are two bases.
10. (L.O.1,L.O.2) Determine all values m∈Rto make sure that Eis a basis of R3.
Am=−2B None of the others C m= 41 Dm= 13 Em= 40
11. (L.O.1,L.O.2) Let m= 0.Find the coordinate vector of a vector uwith respect to the basis F,
given that the coordinate vector of uwith respect to the basis Eis [u]E=
1
2
3
.
A
−13
14
−9
B
−7
10
−13
C None of the others D
−10
23
−23
E
0
1
−19
Questions 12 through 13
In the vector space M3×2(R)(the set of all real matrices size of 3×2),
let V={X∈M3×2(R)|XA = 0}be a subspace of M3×2(R)where A=1 2
3 6.
Stu. Fullname: Stu. ID: Page 2 of 4
Midterm Exam
- MT1007 3131 - 12:00 Semester 1 - October 28th, 2023
12. (L.O.1,L.O.2) Find all values m∈Rsuch that
−6 2
m2
−m−6 0
∈V.
Am=−6B None of the others C m= 0 Dm=−4Em= 1
13. (L.O.1,L.O.2) Find the dimension of V.
A5B1C None of the others D 3E6
Questions 14 through 17
Assume that the input-output matrix of a economic system with 3 sectors: Industry, Agriculture, Service
is given as below: A=
0.1 0.1 0.1
0.1 0.15 0.1
0.15 0.2m
, m ∈R.Let B= 20A. Given that the output values (in the
order: Industry, Agriculture, Service) of each sector is 60,40,50 (billion USD).
14. (L.O.1,L.O.2) Find all values m∈Rsuch that Ais invertible.
Am= 3/20 Bm= 11/40 Cm= 1/5Dm= 1/4Em= 1/3
15. (L.O.1,L.O.2) What is the total value of products supplied by the industry to the agricultural sector
in billions of USD?
A4B6.5C None of the others D 6E5.5
16. (L.O.1,L.O.2) Find the total input values (billion USD) of the industry sector (the total value that
all sectors supply to the industry )?
A14.0B None of the others C 18.5D23.2E21.0
17. (L.O.1,L.O.2) For a sector, let out := the total output value and in := the total input value. Then
the profit margin is defined by: roe =out -in
in ·100% . Compute the profit margin of the industry
sector.
A162.71% B None of the others C 185.71% D241.71% E96.71%
Questions 18 through 20
Given the life span of a population of species is 9 months (after 9 months it will be sold). This population
is divided into 3 classes: 0<age ≤3 (I),3≤age <6 (II),6≤age <9 (III). The average numbers of
offsprings produced in 3 months by the age class I, II, III are: 1.0, 6, 2, respectively. The probabilities
of survival after 3 months of the age classes I and II are 80% and 90%, respectively. Suppose that at
the initial moment, one has 100 individuals in age class I while there is not any individual in classes II
and III.
18. (L.O.1,L.O.2) Find the Leslie matrix L.
A
1.0 6.0 2.0
0.8 0.0 0.0
0.0 0.9 0.0
B
0.0 2.0 2.0
0.8 0.0 0.0
0.0 0.9 0.0
C
0.0 6.0 2.0
0.8 0.0 0.0
0.0 0.9 1.0
D
1.0 6.0 2.0
0.8 0.0 0.2
0.0 0.9 0.1
E None of the others
19. (L.O.1,L.O.2) After 1 year, how many individuals are there in the age class III? (Round the result
to the nearest integer).
A418.0B441.0C404.0D286.0E None of the others
Stu. Fullname: Stu. ID: Page 3 of 4
Midterm Exam
- MT1007 3131 - 12:00 Semester 1 - October 28th, 2023
20. (L.O.1,L.O.2) Each newborn individual will get a vaccination dose. After one year, what is the
total number of doses will have been used? (Round the result to the neareast integer).
A5193.0B None of the others C 1367 D6016.0E9542.0
Stu. Fullname: Stu. ID: Page 4 of 4
Lecturer: Date Approved by: Date
Oct. 16th,
2023
Oct. 16th,
2023
ThS. Phan Thị Khánh Vân
.....................................................................................................
UNIVERSITY OF TECHNOLOGY - VNUHCM
Faculty of Applied Science
Midterm Exam
Academic year 2023-2024 Semester 1
Exam date October 28th, 2023
Course title Linear Algebra Score
Course ID MT1007 Sheet code 3132
Duration 50 minutes Shift 12:00
Instructions to students:
- This is a closed book exam. Only your calculator is allowed. Total available score: 10.
- At the beginning of the working time, you MUST fill in your full name and student ID on this question
sheet. There are 20 questions on 4 pages.
- Do not round between steps. Round your final answers to 4 decimal places.
Student’s full name: ...................................... Invigilator 1: .......................
Student Id: ................... Group: ...... .......... Invigilator 2: .......................
1. (L.O.1,L.O.2) Given two matrices A∈M2×3and B∈M5×5.Let Xand Ysatisfy Y=AXB. Then,
the size of Xis:
A None of the others B X∈M4×4CX∈M3×2DX∈M3×5EX∈M2×5
2. (L.O.1,L.O.2) Find the rank of the matrix A=
1 2 0 2
2−1−1 2
1 2 2 1
1−1 3 4
.
A2B3C None of the others D 1E4
3. (L.O.1,L.O.2) Let Abe the matrix
1 1 1
1 2 3
3 2 2
with the determinant 1. Evaluate det(2A3).
A−8B None of the others C −64 D8E0
4. (L.O.1,L.O.2) In the vector space R3,let mbe a real number and
M={(1,2,1),(2,5,2),(1,2, m),(3,7,3)}
be a vector set. Find msuch that Mis a spanning set of R3.
Am=−2B None of the others C m= 0 Dm= 3 Em= 1
5. (L.O.1,L.O.2) In the vector space P2[x],let mbe a real number and
M={2x2+ 2x+ 1, x2+ 2,2x+m}be a vector set. Find msuch that Mis linearly independent.
Am=−3Bm=−6Cm=−4D None of the others E m=−1
6. (L.O.1,L.O.2) A circuit is given in the following figure.