2
2
Chương 2
Áp dụng cơ học lượng tử vào cấu tạo nguyên tử
2.1 Lí thuyết tóm lược
Kể từ khi sự áp dụng thành công cơ học lượng tử để khảo sát cấu tạo nguyên tử trong hoá
học đã khẳng định tính đúng đắn của lí thuyết lượng tử. Trong chương này chúng ta đề cập tới
một số hệ lượng tử hoá học quan trọng có liên quan đến cấu trúc nguyên tử (Hệ quay tử cứng
nhắc và dao động tử điều hoà được chuyển xuống chương khái quát về phổ phân tử).
2.1.1 Electron chuyển động trong giếng thế
1. Chuyển động của electron trong giếng thế một chiều
Phương trình Schrửdinger trong trường hợp này cú dạng:
Giải phương trình vi phân ta có:
– Hàm sóng ψ
n
(x) =
2
L
sinn
L
π
x
– Năng lượng E
n
= n
2
2
2
h
8mL
;
n =1, 2, 3... số lượng tử chính;
h- hằng số Planck;
m- khối lượng electron;
2
2
d
dx
ψ
+ 2
2m
=
Eψ = 0
Phương trỡnh Schrửdinger trong trường hợp này cú dạng:
Giải phương trình vi phân ta có:
u = 0
0Lx
Vuihoc24h.vn
3
3
– Hàm sóng ψ
n
(x) =
2
L
sinn
L
π
x
– Năng lượng E
n
= n
2
2
2
h
8mL
;
n =1, 2, 3... số lượng tử chính;
h- hằng số Planck;
m- khối lượng electron;
L- chiều rộng giếng thế.
2. Chuyển động của electron trong giếng thế 3 chiều
– Hàm sóng:
xyz
nnn
ψ
(x, y, z) =
x
n
ψ
(x)
y
n
ψ
(y)
z
n
ψ
(z)
với:
x
n
ψ
(x) =
x
2
L
sinn
x
x
L
π
x
y
n
ψ
(y) =
y
2
L
sinn
y
y
L
π
y
z
n
ψ
(z) =
z
2
L
sinn
z
z
L
π
z
– Năng lượng E =
x
n
E
+
y
n
E
+
z
n
E
=
2
h
8m
xyz
2
22
y
xz
222
nnn
n
nn
LLL
⎡
⎤
⎢
⎥
⎢
⎥
++
⎢
⎥
⎢
⎥
⎣
⎦
2.1.2
Bài toán nguyên tử hiđro trong trường xuyên tâm
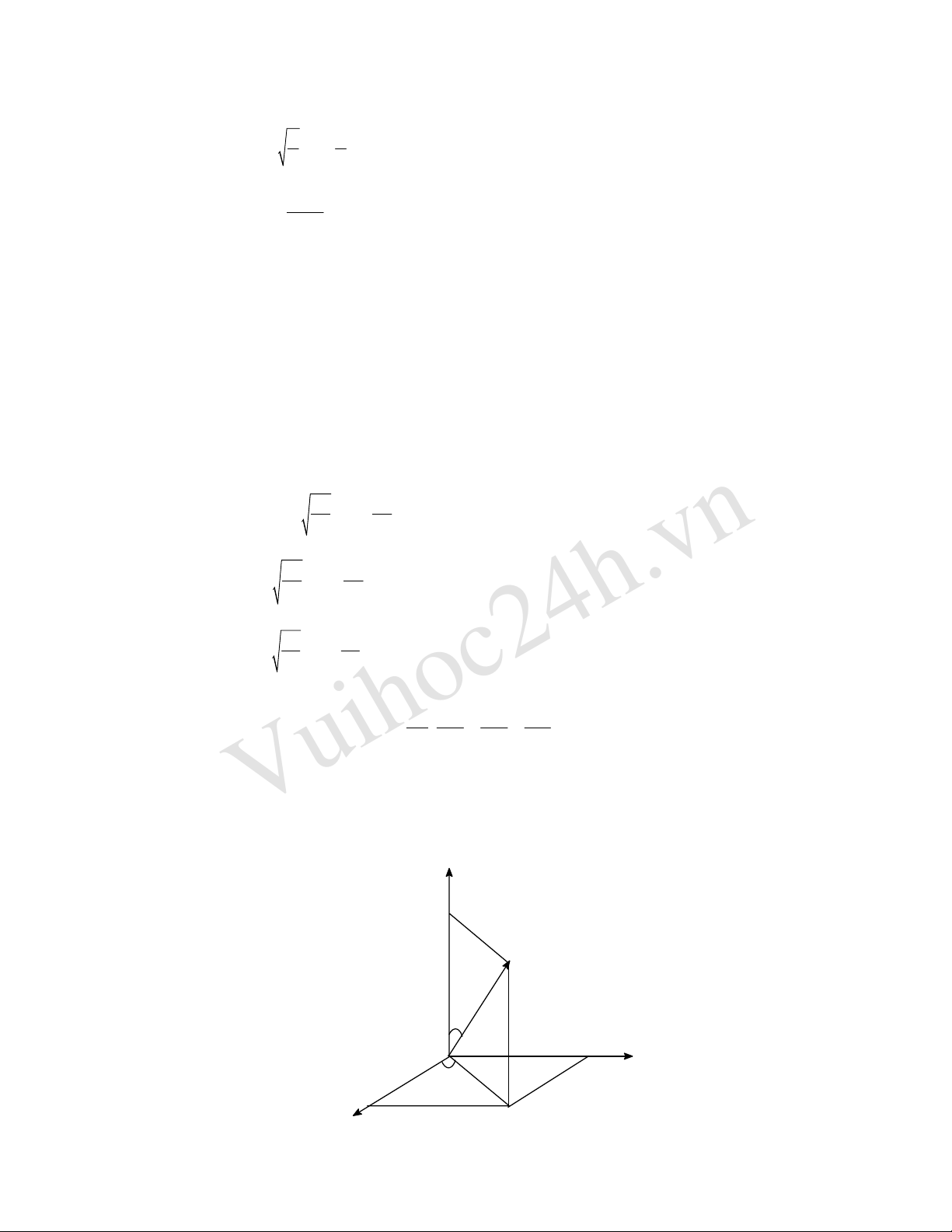
1. Mối tương quan giữa tọa độ Descartes và toạ độ cầu
z = rcosθ
x = rsinθ.cosϕ
y = rsinθ.sinϕ
r
2
= x
2
+ y
2
+ z
2
dτ = r
2
drsinθdθdϕ
x
y
z
θ
ϕ
0
r
Vuihoc24h.vn
4
4
víi: 0 ≤ r < ∞ ;
0 ≤ θ ≤ π ;
0 ≤ ϕ ≤ 2π.
2. Phương trình Schrửdinger ở trạng thái dừng
ˆ
H
ψ(r, θ, ϕ) = Eψ(r, θ, ϕ)
ψ(r, θ, ϕ) = R(r)Y(θ, ϕ)
với:
ˆ
H
= –
2
h
2m
2
r2
1
rΛ
⎛⎞
⎟
⎜∇+ ⎟
⎜⎟
⎟
⎜
⎝⎠
+ U
trong đó:
2
r
∇
=
2
1
r
r
∂
∂
2
rr
⎛⎞
∂⎟
⎜⎟
⎜⎟
⎟
⎜
⎝⎠
∂
Λ =
1
sinθθ
∂
∂sin θθ
⎛⎞
∂⎟
⎜⎟
⎜⎟
⎟
⎜
⎝⎠
∂
+
2
1
sin
θ
2
2
ϕ
∂
∂
Sau khi thay các giá trị tương ứng và thực hiện một số phép biến đổi ta thu được 2
phương trình:
– Phương trình góc:
2
ˆ
M
Y(θ, ϕ) = λ
2
=
Y(θ, ϕ)
– Phương trình bán kính:
d
dr
2
dR
rdr
⎛⎞
⎟
⎜⎟
⎜⎟
⎟
⎜
⎝⎠
+ r
2
2
2m
=
(E – U)R = λR
Ở đây toán tử mômen động lượng có dạng:
z
ˆ
M
= – i
=ϕ
∂
∂
;
2
ˆ
M
= –
2
=
Λ
Các hệ thức giao hoán tử:
[
z
ˆ
M
,
2
ˆ
M
] = 0; [
z
ˆ
M
,
ˆ
H
] = 0; [
2
ˆ
M
,
ˆ
H
] = 0
Giải phương trình góc và bán kính ta thu được các nghiệm sau:
a) Năng lượng: E
n
= –
24
22
mZ e
2n =
k
2
= –13,6
2
2
Z
n
[eV]
b) Hàm sóng:
n, ,m
ψA
A
(r, θ, ϕ) = R
n,
A
(r) .
,m
YA
A
(θ, ϕ)
Vuihoc24h.vn
5
5
hàm AO hàm bán kính hàm góc
n: 1, 2, 3,... n số lượng tử chính
A: 0, 1, 2, 3,... n – 1 số lượng tử phụ
m
A
: 0, ±1, ±2,... ± A số lượng tử từ
k =
o
1
4
πε
= 9.10
9
2
J.m
C
là hệ số tỉ lệ trong tương tác tĩnh điện.
Các giá trị của hàm R(x), hàm Y(θ, ϕ) được ghi thành bảng tại phần phụ lục.
c) Hàm toàn phần
S
n, ,m ,m
ΨA
A
(r, θ, ϕ, σ) =
n, ,m
ψA
A
(r,θ, ϕ) . χ(σ)
hàm toàn phần hàm AO hàm spin
m
s
= ±
1
2
Số lượng tử spin
d) Các giá trị mômen động lượng
– Mômen động lượng: M =
(1)+AA =
– Mômen động lượng hình chiếu: M
z
= m
A
=
– Mômen động lượng spin: M
s
=
s(s 1)+=
– Mômen động lượng toàn phần: M
t.p
=
J(J 1)+=
với: J = A + s gọi là số lượng tử nội.
e) Phổ phát xạ nguyên tử của hiđro
1
λ
=
ν
= R
H22
tc
11
nn
⎛⎞
⎟
⎜⎟
⎜−⎟
⎜⎟
⎜⎟
⎜
⎝⎠
; R
H
- hằng số Rydberg
3. Mật độ xác suất tìm thấy vi hạt theo r và θ, ϕ
a) Theo lí thuyết xác suất
Xác suất có mặt của electron được xác định bằng biểu thức:
dp =⏐ψ⏐
2
dτ với
∫
∫
ψ
2
dτ = 1
Vuihoc24h.vn
6
6
Trong thực tế tính toán người ta thường xác định mật độ xác suất có mặt của electron ở một
điểm M nào đó trong không gian, tại thời điểm t, trong một đơn vị thể tích dτ và được tách riêng
thành 2 phần độc lập.
b) Mật độ xác suất theo bán kính
D(r) =
dp(r)
dr
= ⏐R⏐
2
r
2
Xác suất theo r là: dp(r) = R
*
Rr
2
dr
Với điều kiện chuẩn hoá:
0
∞
∫
R
*
Rr
2
dr = 1
Cũng như R(r), mật độ xác suất D(r) chỉ phụ thuộc vào n và A.
c) Mật độ xác suất theo góc
Đây là sự phân bố mật độ xác suất trong trường xuyên tâm theo một hướng cho trước
được xác định bởi góc θ, ϕ.
dp(θ, ϕ) = Y
*
Ysinθdθdϕ = Y
*
YdΩ
dp( , )
d
θϕ
Ω
= D(θ, ϕ) = Y
*
Y = ⏐Y⏐
2
với điều kiện chuẩn hoá
0
θπ
θ
=
=
∫
2
0
ϕπ
ϕ
=
=
∫
Y
*
Ysinθdθdϕ = 1.
Hàm
,m
YA
A
(θ, ϕ) chỉ phụ thuộc vào các số lượng tử A và m
A
,
độc lập với số lượng tử
chính n.
d) Hàm toàn phần - hàm spin - obitan (ASO)
Khi chú ý đến sự hiệu chỉnh khối lượng m của hệ vi mô theo thuyết tương đối của
Einstein trong quá trình giải phương trình Schrửdinger, ta thấy xuất hiện số lượng tử spin với
giá trị m
s
= ±
1
2
.
Như vậy hàm spin-obitan là:
s
n, ,m ,m
ΨA
A
(r, θ, ϕ, σ) = R
n,
A
(x) .
,m
YA
A
(θ, ϕ) .
s
m
χ
(σ)
Hàm toàn phần hàm bán kính hàm góc hàm spin
Hàm spin-obitan hàm AO
Vuihoc24h.vn