CHNG 5
SC CHU TI NGANG CA CC
5.1 Khái nim chung.
V phng din c hc có th coi mt cc n, cc ng hay mt móng sâu khác nh ging
chìm, móng tr …) chu tác dng ca ti trng ngang H0 và mômen un M0 ti cao trình mt t u
thuc mt bài toán. S khác nhau ca các loi móng này ch là  cng ngang.
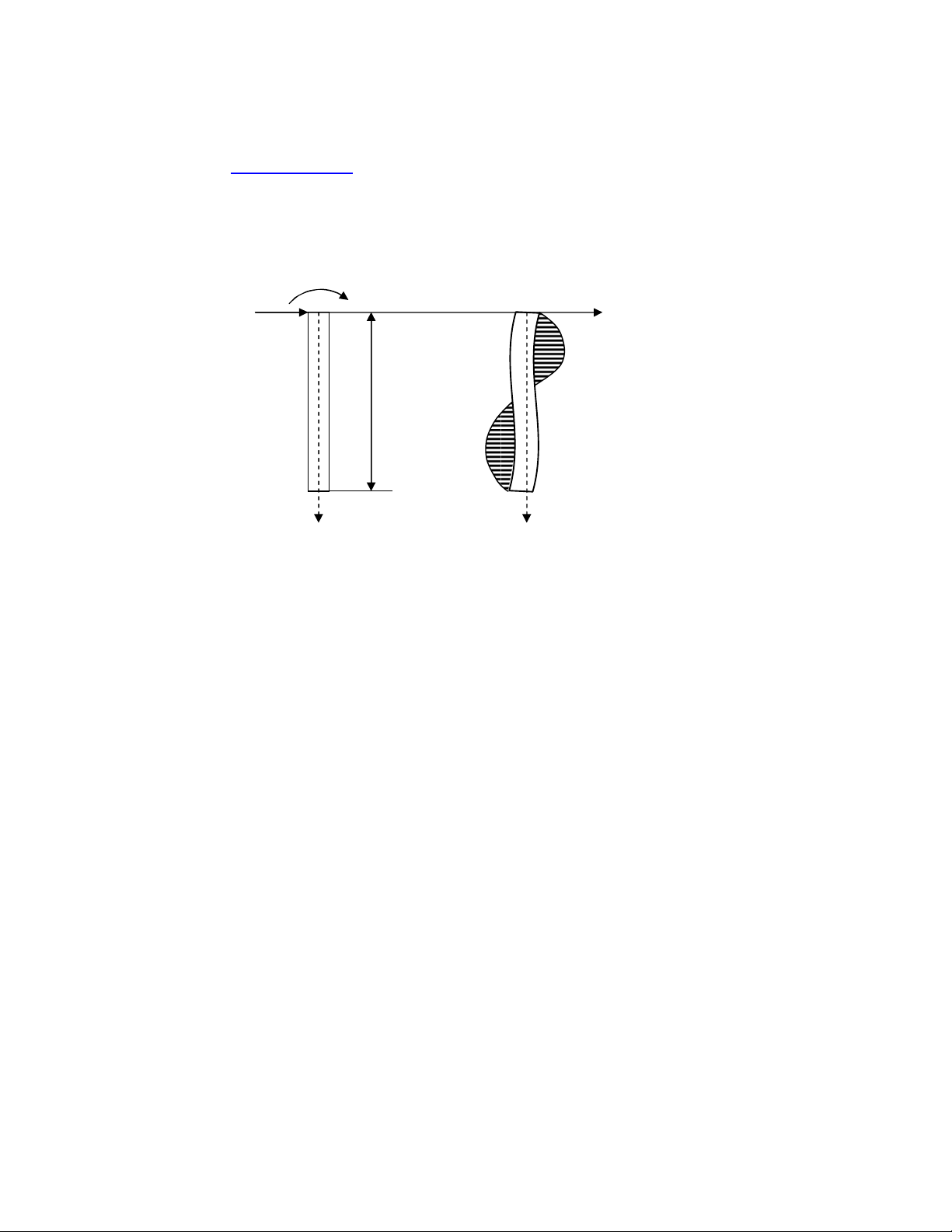
Khi mt móng chu ti trng ngang tác dng thì móng s b chuyn v (un ngang) và ti trng
s c móng truyn lên t ti mt bên và mt áy (tr cc). Nhim v thit k ây là chn móng
sao cho m bo các yêu cu sau:
- chuyn v ngang ca công trình không vt quá tr s gii hn.
- áp lc truyn lên t ti mt bên và áy móng không vt quá tr s gii hn.
- m bo iu kin v cng  bn thân vt liu làm cc (móng).
Nh vy, khi gii bài toán cc (móng sâu) chu ti trng ngang thì phi tìm c các i lng
sau ây:
- chuyn v ngang thay i theo  sâu yz.
- chuyn v xoay ϕz.
- ng sut tác dng lên t theo phng ngang σz.
- ng sut tác dng lên áy móng.
- Mômen un Mz.
- Lc c t Qz.
!ây là bài toán rt phc tp và có ý ngh"a thc t rt ln. Hin nay có rt nhiu phng pháp
gii quyt bài toán này, tuy nhiên có th quy v 3 loi ch yu sau:
- Lp bài toán da vào lý thuyt cân b#ng gii hn ca môi trng ri.
- Lp bài toán da vào lý thuyt nn bin dng cc b (phng pháp h s nn).
- Lp bài toán da vào lý thuyt nn bin dng tng quát.

σ

Ngoài ra, khi gii bài toán này ngi ta còn phân loi thành bài toán móng tuyt i cng (áp
dng cho móng ging chìm, móng tr …) và bài toán móng mm (cc).
Do c thù ca ngành hc, ch tp trung gii thiu bài toán móng mm chu ti trng ngang gii
theo lý thuyt nn bin dng cc b, phng pháp Zavriev.
5.2 Gii bài toán cc chu ti trng ngang theo phng pháp Zavriev.
Phng pháp này da trên các gi thit ch yu sau ây:
1) Nn t c coi nh môi trng àn h$i tuyn tính mà bin dng ca nó c c trng
bi h s nn thay i bc nht theo chiu sâu. Trng hp t có nhiu lp thì tr s m
(c trng ca h s nn) c ly trung bình theo các công thc sau ây:
- Khi chiu sâu nh hng ca móng n#m trong phm vi 2 lp t:
(
)
(
)
2
1 1 2 1
1
2
2m m
tb
m
m h h h m h h
mh
− + −
= (5.1)
- Khi chiu sâu nh hng ca móng n#m trong phm vi 3 lp t:
(
)
(
)
2
1 3 2 1 2 2 3 2 3 3
1
2
2 2
tb
m
m h h h h m h h h m h
mh
+ + + + +
= (5.2)
Trong ó:
- mi = c trng h s nn ca lp t th i, ly theo bng 5.1.
- hi = chiu dày m%i lp t trong phm vi hm.
hm = 2(D+1) (5.3)
- D = ng kính hay cnh cc.
Bng 5.1: h s t l h s nn

 
!
"#$
"%
&#'##()
)'*

+',-
.
/
0-
.
-
-
.

&#'##()%'*
+'-
1
',-
]
23#()'*+41/
"#5'+4'01'6/
.- .!
&#'##()789)9#$'*+41'-/
23#9#$'*:
"#)'+4'01',-/
"#;$'+4'--1',/
-.6 !.0
&#'##9#$'*:
"#<'+4'--1',/
6.= 0.
2) Có k n nh hng ca phn lc t ti áy móng trên hình dáng tit din ca nó.
3) Khi tính phn lc ti mt bên ca móng thì coi móng nh mt kt cu có tit din ch& nht
vi chiu rng tính toán btt làm vic trong iu kin bài toán ph'ng. Chiu rng tính toán
xác nh theo công thc:
1 2
tt
b k k b
= (5.4)
Trong ó:
=
- k1 = h s kinh nghim, xét ti nh hng ca mt c t ngang ca móng i vi s chng (
ca t, ly theo bng 5.2.
- k2 = h s k n s làm vic khác nhau gi&a bài toán không gian và bài toán ph'ng, xác nh
theo công thc kinh nghim:
2
1
1k
b
= +
(5.5)
- b = chiu rng thc ca cc (móng) theo phng th'ng góc vi lc ngang.
4) B) qua nh hng ca ma sát gi&a t và móng.
5) ! có th dùng c các phng trình c hc thông thng, phi gi thit mi tit din
cc luôn luôn ph'ng trc và sau khi chu un.
Phng trình trc un ca cc chu ti trng ngang có dng sau:
( )
4
4
0
zz
y
d y
EI
dz
σ
+ =
(5.6)
Trong ó:
EI =  cng chu un ca tit din ngang cc.
z
y
σ
= phn lc ca t ti mt bên móng.
y(z) và
z
y
σ
u là nh&ng *n s cn tìm. Vì vy cn phi có thêm phng trình th 2. Theo phng pháp
h s nn thì phng trình th 2 có dng:
( )
. . .
z
y tt
z
b m z y
σ
= (5.7)
Thay (5.7) vào (5.6) có c
( )
( )
4
4
. . . 0
z
tt z
d y
EI b m z y
dz
+ =
(5.8)
Gii phng trình (5.8) s c hàm y(z) là phng trình  võng ca cc, t ó s xác nh c các
i lng khác.
Zavriev dùng li gii da vào phng pháp thông s ban u ca Urban, có c kt qu;
( )
0 0 0
0 1 1 1 1
2 3
z
M H
y y A B C D
EI EI
ϕ
α α α
= + + + (5.9)
!
Trong ó:
y0 = chuyn v ngang ca móng ti mt t.
ϕ0 = chuyn v xoay ca móng ti mt t.
α = h s rút ra trong quá trình gii bài toán:
5
tt
mb
EJ
α
= (5.10)
A1, B1, C1, D1 = các hàm s ph thuc vào ta  không th nguyên
.
z z
α
=
và c gi là
các hàm nh hng:
5 10 15
1
6 11 16
1
2 7 12 17
1
3 8 13 18
1
1 6 6.11 ...
5! 10! 15!
2 2.7 2.7.12 ...
6! 11! 16!
3 3.8 3.8.13 ...
2! 7! 12! 17!
4 4.9 4.9.14 ...
3! 8! 13! 18!
z z z
A
z z z
B z
z z z z
C
z z z z
D
= − + − +
= − + − +
= − + − +
= − + − +
(5.11)
Ly vi phân bc 1, 2 và 3 phng trình (5.9) ta s c các phng trình góc xoay, mômen un và lc
c t nh sau:
( )
0 0 0
0 2 2 2 2
2 3
zM H
y A B C D
EI EI
ϕ
ϕ
α α α α
= + + + (5.12)
( )
0 0 0
0 3 3 3 3
2 2 3
z
MM H
y A B C D
EI EI EI
ϕ
α α α α
= + + + (5.13)
( )
0 0 0
0 4 4 4 4
3 2 3
z
QM H
y A B C D
EI EI EI
ϕ
α α α α
= + + + (5.14)
Trong ó Ai, Bi, Ci, Di (i=2÷4) tng ng là o hàm bc i-1 ca A1, B1, C1, D1.
Khi ã có y(z) thì phn lc ngang
z
y
σ
>c xác nh nh sau:
( )
0 0 0
0 1 1 1 1
2 3
z
y z z
M H
C y mz y A B C D
EI EI
ϕ
σα α α
= = + + +
(5.15)
Nh vy, nu tìm c các thông s ban u y0, ϕ0 và bit ti trng t ti u cc là M0 và H0 thì s
tìm c các i lng khác.
! xác nh y0 và ϕ0 phi da vào iu kin biên ca bài toán. Tùy trng hp cc có ngàm hay không
ngàm vào tng á mà iu kin biên s khác nhau;
- Khi móng không ngàm sâu vào tng á mà ch i qua nh&ng lp t thông thng thì iu
kin biên ca bi toán s là:
0
h c
h
M M
Q
=
=
(5.16)
-
- Khi móng ngàm sâu vào tng á thì iu kin biên ca bi toán s là:
0
0
h
h
y
ϕ
=
=
(5.17)
Trong ó:
yh, ϕh, Mh, Qh = chuyn v ngang, chuyn v xoay, mômen un và lc c t ti tit din
áy móng (m+i cc) (z = h).
Mc = momen cn do phn lc ca t ti áy móng gây ra, '
c h h d
M C I
ϕ
= −
'
h
C
= h s nn theo phng th'ng ng ca t ti chiu sâu z = h.
I = momen quán tính ca tit din áy móng (m+i cc).
Di ây s trình bày cách xác nh y0 và ϕ0 cho 2 trng hp ã nêu ra:
5.2.1 Trng hp móng không ngàm vào tng á.
Ký hiu
0
ik
δ
là chuyn v n v ca móng ti cao trình mt t, c th là:
0
HH
δ
= chuyn v ngang do H0 = 1 gây ra.
0
HM
δ
= chuyn v ngang do M0 = 1 gây ra.
0
MM
δ
= chuyn v xoay do M0 = 1 gây ra.
0
MH
δ
= chuyn v xoay do H0 = 1 gây ra.
Theo quan h c hc thì y0 và ϕ0 s tìm c nh sau:
0 0
0 0 0
HH HM
y H M
δ δ
= + (5.18)
(
0 0
0 0 0
MH MM
H M
ϕ δ δ
= − + (5.19)
Du tr trong công thc 5.19 là do quy nh v du khác so vi quy c du trong môn SBVL.
Nh vy, mun tìm y0 và ϕ0 thì phi tìm c bn *n s
0
HH
δ
,
0
HM
δ
,
0
MM
δ
,
0
MH
δ
, trong khi ch có 2
phng trình (là iu kin biên 5.16). ! thc hin c ta phi tìm cách 5.16 ch xut hin 2 *n s.
Cách làm là cho ln lt H0 = 1 còn M0 = 0 và M0 = 1 còn H0 = 0 sau ó s, dng iu kiên biên 5.16
s xác nh ln lt các *n s tng ng.
a) Trng hp H0 = 1 và M0 = 0.
Chú ý r#ng, công thc 5.12, 5.13, 5.14 dùng xác nh ϕ(z), M(z), Q(z) úng cho trng hp tng quát
(H và M bt k-) thì c+ng s úng cho trng hp H0 = 1 và M0 = 0, khi ó y0 =
0
HH
δ
và ϕ0 =
0
MH
δ
.
Nh vy iu kin biên s có dng sau;
'
0 0
0 0
3 3 3 2 2 2
3 3
0
0
4 4 4
3
1 1
10
h d
MH MH
HH HH
MH
HH
C I
A B D A B D
EI EI EI
A B D
EI
δ δ
δ δ
α α α α α
δ
δα α
+ + = − + +
+ + =
(5.20)