CH NG 7: GI I PH NG TRÌNH VI PHÂNƯƠ Ả ƯƠ
§1. BÀI TOÁN CAUCHY
M t ph ng trình vi phân c p 1 có th vi t d i d ng gi i đcộ ươ ấ ể ế ướ ạ ả ượ
y=f(x,y) mà ta có th tìm đc hàm y t đo hàm c a nó. T n t i vô sể ượ ừ ạ ủ ồ ạ ố
nghi m tho mãn ph ng trình trên. M i nghi m ph thu c vào m t h ngệ ả ươ ỗ ệ ụ ộ ộ ằ
s tu ý. Khi cho tr c giá tr ban đu c a y là yố ỳ ướ ị ầ ủ o t i giá tr đu xạ ị ầ o ta nh nậ
đc m t nghi m riêng c a ph ng trình. Bài toán Cauchy (hay bài toán cóượ ộ ệ ủ ươ
đi u ki n đu) tóm l i nh sau: cho x sao cho b ề ệ ầ ạ ư x a, tìm y(x) tho mãnả
đi u ki n:ề ệ
)a(y
)y,x(f)x(y
(1)
Ng i ta ch ng minh r ng bài toán này có m t nghi m duy nh t n u fườ ứ ằ ộ ệ ấ ế
tho mãn đi u ki n Lipschitz:ả ề ệ
2121 yyL)y,x(f)y,x(f
v i L là m t h ng s d ng.ớ ộ ằ ố ươ
Ng i ta cũng ch ng minh r ng n u fườ ứ ằ ế y ( đo hàm c a f theo y ) là liênạ ủ
t c và b ch n thì f tho mãn đi u ki n Lipschitz.ụ ị ặ ả ề ệ
M t cách t ng quát h n, ng i ta đnh nghĩa h ph ng trình b c 1:ộ ổ ơ ườ ị ệ ươ ậ
)y,...,y,y,x(fy
)y,...,y,y,x(fy
)y,...,y,y,x(fy
n21nn
n2122
n2111
Ta ph i tìm nghi m yả ệ 1, y2,..., yn sao cho:
)a(Y
)X,x(f)x(Y
v i:ớ
n
2
1
y
..
..
y
y
Y
n
2
1
f
..
..
f
f
F
n
2
1
y
..
..
y
y
Y
N u ph ng trình vi phân có b c cao h n (n), nghi m s ph thu cế ươ ậ ơ ệ ẽ ụ ộ
vào n h ng s tu ý. Đ nh n đc m t nghi m riêng, ta ph i cho n đi uằ ố ỳ ể ậ ượ ộ ệ ả ề
ki n đu. Bài toán s có giá tr đu n u v i giá tr xệ ầ ẽ ị ầ ế ớ ị o đã cho ta cho y(xo),
y(xo), y(xo),....
168
M t ph ng trình vi phân b c n có th đa v thành m t h ph ngộ ươ ậ ể ư ề ộ ệ ươ
trình vi phân c p 1. Ví d n u ta có ph ng trình vi phân c p 2:ấ ụ ế ươ ấ
)a(y,)a(y
)y,y,x(fy
Khi đt u = y và v = yặ ta nh n đc h ph ng trình vi phân c p 1:ậ ượ ệ ươ ấ
v i đi u ki n đu: u(a) = ớ ề ệ ầ và v(a) =
Các ph ng pháp gi i ph ng trình vi phân đc trình bày trongươ ả ươ ượ
ch ng này là các ph ng pháp r i r c: đo n [a, b] đc chia thành n đo nươ ươ ờ ạ ạ ượ ạ
nh b ng nhau đc g i là các "b c" tích phân h = ( b - a) / n.ỏ ằ ượ ọ ướ
§2. PH NG PHÁP EULER VÀ EULER C I TI NƯƠ Ả Ế
Gi s ta có ph ng trình vi phân:ả ử ươ
)a(y
)y,x(f)x(y
(1)
và c n tìm nghi m c a nó. Ta chia đo n [xầ ệ ủ ạ o,x ] thành n ph n b i các đi mầ ở ể
chia:
xo < x1 < x2 <...< xn = x
Theo công th c khai tri n Taylor m t hàm lân c n xứ ể ộ ậ i ta có:
)x(y
6
)xx(
)x(y
2
)xx(
)x(y)xx()x(y)x(y i
3
i1i
i
2
i1i
ii1ii1i
N u (xếi+1 - xi) khá bé thì ta có th b qua các s h ng (xể ỏ ố ạ i+1 - xi)2 và các s h ngố ạ
b c cao ậ
y(xi+1) = y(xi) + (xi+1- xi)y(xi)
Tr ng h p các m c cách đu: ườ ợ ố ề
(xi-1 - xi) = h = (x - xo)/ n
thì ta nh n đc công th c Euler đn gi n:ậ ượ ứ ơ ả
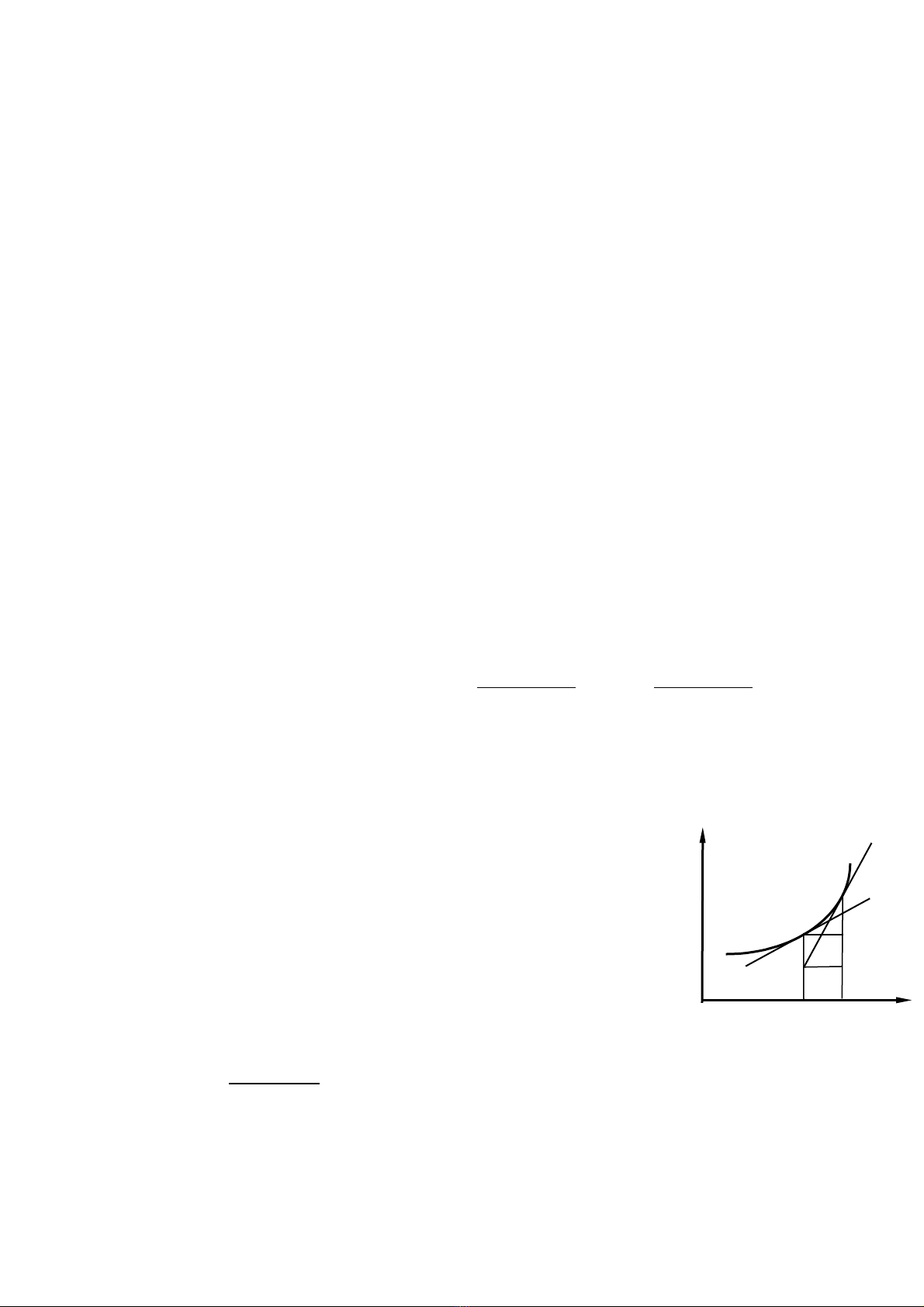
yi+1 = yi + hf(xi, yi) (2)
V m t hình h c ta th y (1) cho k t qu càngề ặ ọ ấ ế ả
chính xác n u b c h càng nh .ế ướ ỏ
Đ tăng đ chính xác ta có th dùng công th c Euler c i ti n. Tr c h t taể ộ ể ứ ả ế ướ ế
nh c l i đnh lí Lagrange: ắ ạ ị gi s f(x) là hàm liên t c trong [a, b] và kh vi trongả ử ụ ả
(a,b) thì có ít nh t m t đi m c ấ ộ ể
(a ,b) đ choể:
ab
)a(f)b(f
)c(f
Theo đnh lí Lagrange ta có :ị
))c(y,c(hf)x(y)x(y iii1i
Nh v y v i c ư ậ ớ (xi, xi+1) ta có th thay :ể
169
y
x
xixi+1
yi
yi+1
)y,x(f)y,x(f
2
1
))c(y,c(f 1i1iiiii
T đó ta có công th c Euler c i ti n :ừ ứ ả ế
)y,x(f)y,x(f
2
h
yy 1i1iiii1i
(3)
Trong công th c này giá tr yứ ị i+1 ch a bi t. Do đó khi đã bi t yư ế ế i ta ph i tìm yải+1
b ng cách gi i ph ng trình đi s tuy n tính (3). Ta th ng gi i (3) b ngằ ả ươ ạ ố ế ườ ả ằ
cách l p nh sau: tr c h t ch n x p x đu tiên c a phép l p ặ ư ướ ế ọ ấ ỉ ầ ủ ặ
)0(
1i
y
chính là
giá tr yịi+1 tính đc theo ph ng pháp Euler sau đó dùng (3) đ tính các ượ ươ ể
)s(
1i
y
,
c th là:ụ ể
)y,x(f)y,x(f
2
h
yy
)y,x(hfyy
)1s(
1i1iiii
)s(
1i
iii
)0(
1i
Quá trình tính k t thúc khi ế
)s(
i
y
đ g n ủ ầ
)1s(
i
y
Ch ng trình gi i ph ng trình vi phân theo ph ng pháp Euler nh sau:ươ ả ươ ươ ư
Ch ng trình 7-1ươ
/ / p p_Euler;
#include <conio.h>
#include <stdio.h>
#include <math.h>
float f(float x,float y)
{
float a=x+y;
return(a);
}
void main()
{
int i,n;
float a,b,t,z,h,x0,y0,c1,c2;
float x[100],y[100];
clrscr();
printf("Cho can duoi a = ");
scanf("%f",&a);
printf("Cho can tren b = ");
scanf("%f",&b);
printf("Cho so buoc tinh n = ");
scanf("%d",&n);
170
printf("Cho so kien x0 = ");
scanf("%f",&x0);
printf("Cho so kien y0 = ");
scanf("%f",&y0);
printf("\n");
printf("Bang ket qua \n");
printf("\n");
printf("Phuong phap Euler \n");
h=(b-a)/n;
x[1]=x0;
y[1]=y0;
printf(" x y");
printf("\n");
for (i=1;i<=n+1;i++)
{
x[i+1]=x[i]+h;
y[i+1]=y[i]+h*f(x[i],y[i]);
printf("%3.2f%16.3f",x[i],y[i]);
printf("\n");
}
printf("\n");
getch();
printf("Phuong phap Euler cai tien\n");
printf(" x y");
printf("\n");
for (i=1;i<=n+1;i++)
{
x[i+1]=x[i]+h;
c1=h*f(x[i],y[i]);
c2=h*f(x[i]+h,y[i]+c1);
y[i+1]=y[i]+(c1+c2)/2;
printf("%3.2f%15.5f",x[i],y[i]);
printf("\n");
}
getch();
}
V i ph ng trình cho trong function và đi u ki n đu xớ ươ ề ệ ầ o = 0, yo = 0,
nghi m trong đo n [0, 1] v i 10 đi m chia là:ệ ạ ớ ể
x y(Euler) y(Euler c i ti n)ả ế
0.0 0.00 0.00
0.1 0.00 0.01
171
0.2 0.01 0.02
0.3 0.03 0.05
0.4 0.06 0.09
0.5 0.11 0.15
0.6 0.17 0.22
0.7 0.25 0.31
0.8 0.34 0.42
0.9 0.46 0.56
1.0 0.59 0.71
§3. PH NG PHÁP RUNGE - KUTTAƯƠ
Xét bài toán Cauchy (1). Gi s ta đã tìm đc giá tr g n đúng yả ử ượ ị ầ i c aủ
y(xi) và mu n tính yối+1 c a y(xủi+1). Tr c h t ta vi t công th c Taylor:ướ ế ế ứ
)c(y
!m
h
)x(y
!m
h
)x(y
2
h
)x(yh)x(y)x(y )1m(
1m
i
)m(
m
i
2
ii1i
(11)
v i c ớ(xi, xi+1) và:
)x(y,xf)x(y
iii
)x(y,xf
dx
d
)x(y ii
1k
1k
i
)k(
Ta vi t l i (11) d i d ng:ế ạ ướ ạ
)c(y
!m
h
)x(y
!m
h
)x(y
2
h
)x(yhyy )1m(
1m
i
)m(
m
i
2
ii1i
(12)
Ta đã kéo dài khai tri n Taylor đ k t qu chính xác h n. Đ tính yể ể ế ả ơ ể i, yi v.v.
ta có th dùng ph ng pháp Runge-Kutta b ng cách đt:ể ươ ằ ặ
)i(
44
)i(
33
)i(
22
)i(
11i1i krkrkrkryy
(13)
trong đó:
.......
)kky,bhx(hfk
)ky,ahx(hfk
)y,x(hfk
)i(
2
)i(
1ii
)i(
3
)i(
1ii
)i(
2
ii
)i(
1
(14)
và ta c n xác đnh các h s a, b,..; ầ ị ệ ố , , ,...; r1, r2,.. sao cho v ph i c a (13)ế ả ủ
khác v i v ph i c a (12) m t vô cùng bé c p cao nh t có th có đi v i h.ớ ế ả ủ ộ ấ ấ ể ố ớ
Khi dùng công th c Runge-Kutta b c hai ta có:ứ ậ
)ky,ahx(hfk
)y,x(hfk
)i(
1ii
)i(
2
ii
)i(
1
(15)
và
)i(
22
)i(
11i1i krkryy
(16)
Ta có:
y(x) = f[x,y(x)]
)x(y,xf)x(y,xf)x(y yx
172