1
CHUYÊN ĐỀ. ĐIỂM – ĐƯỜNG THẲNG – ĐOẠN THẲNG – TAM GIÁC.
PHẦN I.TRỌNG TÂM CẦN ĐẠT
A. KIẾN THỨC CẦN NHỚ.
I. ĐIỂM, ĐƯỜNG THẲNG, BA ĐIỂM THẲNG HÀNG
1.Vịtrícủađiểmvàđườngthẳng
-Điểm
A
thuộcđườngthẳng
a
,kíhiệu
A a
-Điểm
B
khôngthuộcđườngthẳng
a
,kíhiệu
B a
2.Bađiểmthẳnghàngkhichúngcùngthuộcmộtđườngthẳng,bađiểmkhôngthẳnghàngkhichúng
khôngcùngthuộcbấtkìđườngthẳngnào.
3.Trongbađiểmthẳnghàngcómộtđiểmvàchỉmộtđiểmnằmgiữahaiđiểmcònlại.
4.Nếucómộtđiểmnằmgiữahaiđiểmkhácthìbađiểmđóthẳnghàng.
5.Quanhệbađiểmthẳnghàngcònđượcmởrộngthànhnhiều
(4,5,6,....)
điểmthẳnghàng.
II. ĐƯỜNG THẲNG ĐI QUA HAI ĐIỂM
1.Cómộtđườngthẳngvàchỉcó
1
đườngthẳngđiquahaiđiểm
A
và
B
2.Cóbacáchđặttênđườngthẳng:
-Dùngmộtchữcáiinthường:vídụ
a
-Dùnghaichữcáiinthường:vídụ
xy
-Dùnghaichữcáiinhoa:vídụ
AB
3.Bavịtrícóhaiđườngthẳngphânbiệt:
-Hoặckhôngcóđiểmchungnào(gọilàhaiđườngthẳngsongsong)
-Hoặcchỉcómộtđiểmchung(gọilàđườngthẳngcắtnhau)
4.Muốnchứngminhhaihaynhiềuđườngthẳngtrùngnhautachỉcầnchứngtỏchúngcóhaiđiểm
chung.
5.Ba(haynhiều)đườngthẳngcùngđiquamộtđiểmgọilàba(haynhiều)đườngthẳngđồngquy.
Muốnchứngminhnhiềuđườngthẳngđồngquytacóthểxácđịnhgiaođiểmcủađườngthẳngnàođó
rồichứngminhcácđườngthẳngcònlạiđềuđiquagiaođiểmnày.
III. TIA
1.Hìnhgồmđiểm
O
vàmộtphầnđườngthẳngbịchiarabởiđiểm
O
đượcgọilàmộttiagốc
O
.
2.Haitiachunggốctạothànhđườngthẳngđượcgọilàhaitiađốinhau
3.Quanhệgiữamộtđiểmnằmgiữahaiđiểmvớihaitiađốinhau,haitiatrùngnhau:
Xét
3
điểm
, ,
A O B
thẳnghàng.
-Nếu
OA
và
OB
đốinhauthìgốc
O
nằmgiữa
A
và
B
-Ngượclạinếu
O
nằmgiữa
A
và
B
thì:
2
+Haitia
,
OA OB
đốinhau
+Haitia
,
AO AB
trùngnhau;haitia
,
BO BA
trùngnhau.
IV. ĐOẠN THẲNG, ĐỘ DÀI ĐOẠN THẲNG, CỘNG ĐỘ DÀI HAI ĐOẠN THẲNG
1.Đoạnthẳng
AB
làhìnhgồmđiểm
A
,điểm
B
vàtấtcảcácđiểmnằmgiữa
A
và
B
2.Mỗiđoạnthẳngcómộtđộdài.Độdàiđoạnthẳnglàmộtsốdương.
3.
AB CD AB
và
CD
cócùngđộdài
AB CD AB
ngắnhơn
CD
AB CD AB
dàihơn
CD
.
4.Điểmnằmgiữahaiđiểm:
Nếuđiểm
M
nằmgiữađiểm
A
vàđiểm
B
thì
AM MB AB
Ngượclại,nếu
AM MB AB
thìđiểm
M
nằmgiữahaiđiểm
A
và
B
.
Nếu
AM MB AB
thìđiểm
M
khôngnằmgiữa
A
và
B
.
Nếuđiểm
M
nằmgiữahaiđiểm
A
và
B
;điểm
N
nằmgiữahaiđiểm
M
và
B
thì
AM MN NB AB
V. VẼ ĐOẠN THẲNG CHO BIẾT ĐỘ DÀI
1.Trêntia
Ox
baogiờcũngvẽđược
1
vàchỉmộtđiểm
M
saocho
OM a
(đơnvịdài).
2.Trêntia
Ox
, ,
OM a ON b
,nếu 0
a b
hayOM<ONthìđiểm
M
nằmgiữahaiđiểm
O
và
N
3.Trêntia
Ox
có
3
điểm
, ,
M N P
; ; ;
OM a ON b OP c
;nếu0
a b
<chayOM<ON<OP
điểm
N
nằmgiữahaiđiểm
M
và
P
.
VI. TRUNG ĐIỂM CỦA ĐOẠN THẲNG
1.Trungđiểmcủađoạnthẳnglàđiểmnằmgiữahaiđầuđoạnthẳngvàcáchđềuhaiđầuđoạnthẳngđó.
2.Nếu
M
làtrungđiểmcủađoạnthẳng
AB
thì
2
AB
MA MB
3.Nếu
M
nằmgiữahaiđầuđoạnthẳng
AB
và
2
MA thì
M
làtrungđiểmcủa
AB
4.Mỗiđoạnthẳngcó
1
trungđiểmduynhất.
VII. TAM GIÁC
1. Định nghĩa
Tamgiác
ABC
làhìnhgồmbađoạnthẳng
, ,
AB BC AC
khibađiểm
, ,
ABC
không
thẳnghàng.Kíhiệulà
ABC
.
2. Các yếu tố trong tam giác
Tamgiác
ABC
có:
+Bađỉnhlà:
, ,
A B C
.
A
B
C
3
+Bacạnhlà:
, ,
AB BC AC
.
+Bagóclà
, ,
ABC BAC ACB
.
3. Để vẽ một tam giác
ABC
có độ dài 3 cạnh cho trước, ta làm như sau:
Bước1.Vẽmộtđoạnthẳng
AB
cóđộdàibằngmộtcạnhchotrước;
Bước2.Vẽđỉnh
C
(thứba)làgiaođiểmcủahaicungtròncótâmlầnlượtlàhaiđỉnh
A
và
B
đãvẽ
vàbánkínhlầnlượtbằngđộdàihaicạnhcònlại.
B. CÁC DẠNG BÀI TẬP
Dạng 1: Bài toán trồng cây thẳng hàng.
- Các cây thẳng hàng là các cây cùng nằm trên một đường thẳng.
- Giao điểm của hai hay nhiều đường thẳng là vị trí của 1 cây thỏa mãn bài toán.
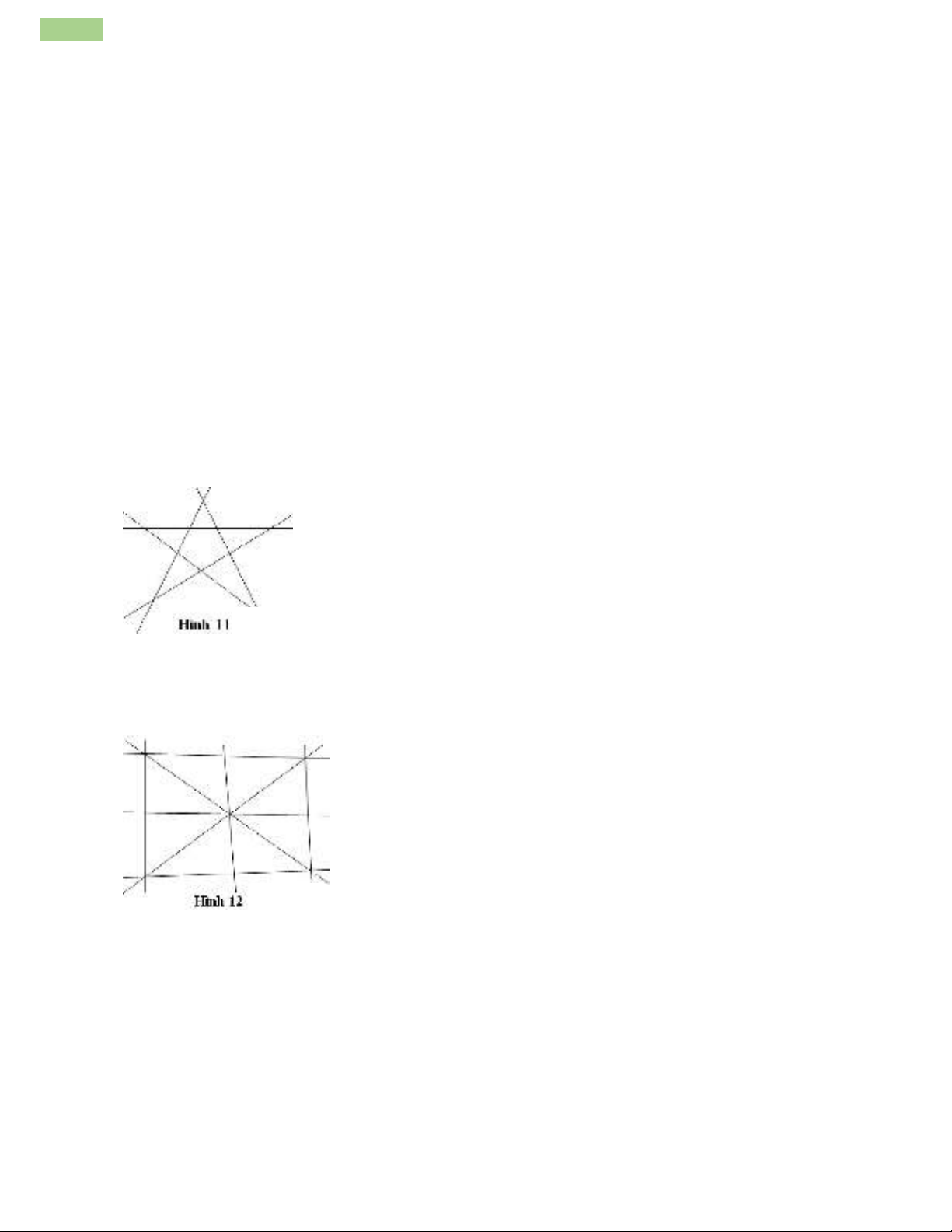
Bài tập 1.Có10cây,hãytrồngthành5hàngsaochomỗihàngcó4cây.
Hướng dẫn
Theohình11(mỗiđiểmtrênhìnhvẽlàmộtcây).
Bài tập 2.Có9cây,hãytrồngthành8hàngsaochomỗihàngcó3cây.
Hướng dẫn
Theohình12(mỗiđiểmtrênhìnhvẽlàmộtcây).
Bài tập 3. Hãyvẽsơđồtrồng10câythành5hàng,mỗihàng4cây(Giảibằng4cách)
Hướng dẫn
Hình
Hình
4
Cách1
Cách2
Cách3
Cách4
Dạng 2: Đếm số đoạn thẳng (đường thẳng) tạo thành từ các điểm cho trước
Cho biết có n điểm (n
∈
N và n ≥ 2).
Kẻ từ một điểm bất kỳ với
n
1
điểm còn lại được
1
n
đoạn thẳng (đường thẳng)
Làm như vậy với
n
điểm nên có
1
n n
đoạn thẳng (đường thẳng). Nhưng mỗi đoạn thẳng (đường
thẳng) được tính
2
lần
Do vậy số đoạn thẳng (đường thẳng) vẽ được là
n n :
1 2
đoạn thẳng (đường thẳng)
Bài tập 1.LấynămđiểmM,N,P,Q,R,trongđókhôngcóbađiểmnàothẳnghàng.Kẻcácđường
thẳngđiquacáccặpđiểmđó.Cóbaonhiêuđườngthẳngtấtcả?Đólànhữngđườngthẳngnào?
Hướng dẫn
Cách1:Vẽhìnhrồiliệtkêcácđườngthẳngđó(Chỉdùngkhichỉcóítđiểm)
Cách2:Bằngcáchtính:
Lấymộtđiểmbấtkì(chẳnghạnđiểmM),cònlại4điểmphânbiệttanốiđiểmMvới4điểmcònlại
đóđược4đườngthẳng.
Với5điểmđãchotacó:4đường×5điểm.
Nhưngvớicáchlàmtrên,mỗiđườngtađãtínhhailần.chẳnghạn,khichọnđiểmMtanốiMvớiN,ta
cóđườngthẳngMN.NhưngkhichọnđiểmN,tanốiNvớiM,tacũngcóđườngthẳngNM.Haiđường
thẳngnàytrùngnhaunêntachỉtínhlàmộtđường.
Vậysốđườngthẳngvẽđượclà: 4 5
10
2
(đườngthẳng).
Bài tập 2.Vẽbốnđườngthẳngđôimộtcắtnhau.Sốgiaođiểm(củahaiđườngthẳnghaynhiềuđường
thẳng)cóthểlàbaonhiêu?
5
Hướng dẫn
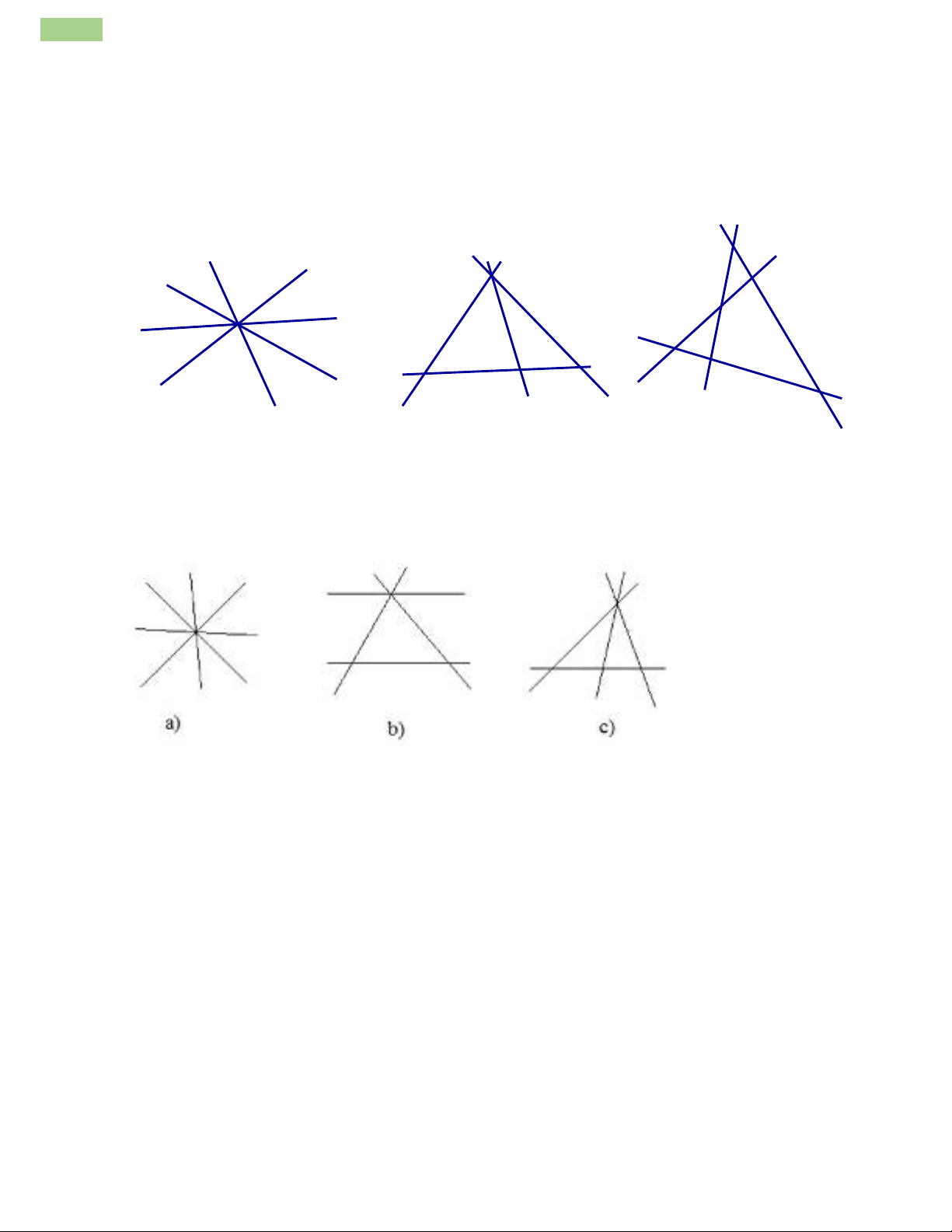
Khivẽbốnđườngthẳngcóthểxảyracáctrườnghợpsau:
a)Bốnđườngthẳngđóđồngquy:cómộtđiểmchung(H.a).
b)Cóbađườngthẳngđồngquy,cònđườngthẳngthứtưcắtbađườngthẳngđó:có4điểm(H.b).
c)Khôngcóbađườngthẳngnàođồngquy(đôimộtcắtnhau):có6điểm(H.c).
a) b) c)
Hình 3
Bài tập 3: Trênmặtphẳngcóbốnđườngthẳng.Sốgiaođiểmcủacácđườngthẳngcóthểbằngbao
nhiêu?
Hướng dẫn
Bàitoánđòihỏiphảixétđủcáctrườnghợp:
Hình 4
a)Bốnđườngthẳngđồngquy:có
1
giaođiểm(H4a)
b)Cóđúngbađườngthẳngđồngquy:
-Cóhaiđườngthẳngsongsong:
3
giaođiểm(H4b)
-Khôngcóhaiđườngthẳngnàosongsong:
4
giaođiểm(H4c)
b)Khôngcóbađườngthẳngnàođồngquy