C©u I.1)Tacãy’=x-2x-m+1
(x - 1)
2
2(x ¹1).
Ta ph¶i t×m m sao cho y’ ³0 trong c¶ 2 kho¶ng (- ¥;1)vµ (1; +¥)Ûx2-2x-m+1³0
Û∆‘=m£0v× hÖ sè cña x2b»ng 1.
2) Phû¬ng tr×nh tiÖm cËn xiªn lµy=x+m+1.GäiPvµQlµgiao ®iÓm cña ®ûêng tiÖm cËn xiªn víi trôchoµnh vµ trôc tung.
Ta cã:
yp=0Ûxp=-m-1;
xQ=0ÛyQ=m+1.
S=
1
2|OP| . |OQ| = 8
OPQ∆Û|-m-1|.|m+1|=16
Û(m+1)
2=16Ûm1=3hoÆc m2= -5.
3) §Ó ®ûêng th¼ngy=mc¾t®åthÞhµmsèt¹i2®iÓm ph©n biÖt A vµ B th× phû¬ng tr×nh:
x+mx-1
x-1
2
=mph¶i cã 2 nghiÖm ph©n biÖt ¹1
Ûx2=1-mcã 2 nghiÖm ph©n biÖt ¹1Û0¹m<1.(1)
Khi ®ã x1,2 =±1- m
.
OA ⊥OB ÛtÝch hÖ sè gãc cña 2 ® êng th¼ng OA vµ OB b»ng -1
Ûm
x.m
x
12
=-1Ûm
m-1
2
=-1Ûm1,2 =-1 5
2
±.
C¶ 2 nghiÖm ®Òu tháa m·n (1).
4) B¹n h·y tù gi¶i nhÐ!
C©u II.1)§ÆtA=y1
x+1
z+1
y(x + z)
-1
x+1
z
(x + z).
Ta ph¶i chøng minh A£0.
www.khoabang.com.vn LuyÖn thi trªn m¹ng – Phiªn b¶n 1.0
________________________________________________________________________________
Ta cã A=(x+z) y
xz +1
y-1
x-1
z
=(x+z) y + xz - yz - xy
xyz
2
=(x + z)(x - y)(z - y)
xyz £0v× 0<x£y£z.
2) BiÕn ®æi vÕ ph¶i bÊt ®¼ng thøc cÇn chøng minh vµ ¸p dông bÊt ®¼ng thøc C«si cho ba sè ³0
ta cã:
3a3+7b
3=3a
3+3b
3+4b
3³3 3a . 3b . 4b
3333
=3ab 3 3 . 4 9ab
22 2
≥.
C©u III. Gäi S lµ diÖn tÝch tam gi¸c, ta cã
S=1
2(a + b + c)r = 1
2ch Þr
h=c
a+b+c.
V×a+b>cnªn r
h<c
c+c= 0,5.
Ta lu«n cã a2+b
2³2ab Þ2c2³2a2+2b
2↔³a2+b
2+2ab=(a+b)
2Þc2
↔a+bÞr
h³c
c2+c=1
2+1 =2-1
> 0,4.
www.khoabang.com.vn LuyÖn thi trªn m¹ng – Phiªn b¶n 1.0
________________________________________________________________________________
www.khoabang.com.vn LuyÖn thi trªn m¹ng – Phiªn b¶n 1.0
________________________________________________________
C©u IVa.
1) Ta cã
33 2 3
3x 1 A B A B(x 1)
(x 1) (x 1) (x 1) (x 1)
+++
=+ =
+++ +
⇒ 3x + 1 = Bx + A + B
⇒ B3
AB1
=
+=
⇒ A2
B3
=−
=
2) T×m nguyªn hµm cña 3
3x 1
y(x 1)
+
=+ :
332
3x 1 2dx 3dx
dx
(x 1) (x 1) (x 1)
+−
=+=
+++
∫∫∫
32
2(x 1) dx 3(x 1) dx
−−
=− + + + =
∫∫
31 21
11
2. (x 1) 3. (x 1) C
31 21
−+ −+
=− + + + +
−+ −+
= 21
(x 1) 3(x 1) C
−−
+−++.
VËy nguyªn hµm cña
3
3x 1
y(x 1)
+
=+ lµ 2
13
F(x) C
x1
(x 1)
=−+
+
+
C©u Va.
1) Gäi 1
BB lµ ®−êng cao cã ph−¬ng tr×nh : 9x − 3y − 4 = 0
1
CC lµ ®−êng cao cã ph−¬ng tr×nh : x + y − 2 = 0
LËp ph−¬ng tr×nh ®−êng th¼ng AC : ®ã lµ ®−êng th¼ng qua A vµ vu«ng gãc víi 1
BB ; v× hÖ sè
gãc cña ®−êng th¼ng 1
BB lµ k = 3 ⇒ hÖ sè gãc cña ®−êng th¼ng AC lµ k = 1
3
−
⇒ Ph−¬ng
tr×nh c¹nh AC lµ
y − 2 = 1(x 2)
3
−− tøc lµ 3y + x − 8 = 0.
LËp ph−¬ng tr×nh ®−êng th¼ng AB : ®ã lµ ®−êng th¼ng qua A vµ vu«ng gãc víi 1
CC ; hÖ sè
gãc cña ®−êng th¼ng 1
CC lµ −1 ⇒ hÖ sè gãc cña ®−êng th¼ng AB lµ 1 ⇒ Ph−¬ng tr×nh c¹nh
AB lµ y − 2 = x − 2 ⇒y = x.
LËp ph−¬ng tr×nh c¹nh BC :
Gi¶i hÖ x3y80
xy20
+−=
+−=
ta ®−îc täa ®é ®iÓm C (−1, 3) ;
Gi¶i hÖ yx0
9x 3y 4 0
−=
−−=
ta ®−îc täa ®é ®iÓm 22
B,
33



⇒ Ph−¬ng tr×nh c¹nh BC lµ
www.khoabang.com.vn LuyÖn thi trªn m¹ng – Phiªn b¶n 1.0
________________________________________________________
22
yx
33
22
31
33
−−
=
−−−
⇒ 7x + 5y − 8 = 0
2) Gi¶ sö hÖ sè gãc cña ®−êng th¼ng cÇn t×m lµ 1
k, hÖ sè gãc cña ®−êng th¼ng AC lµ
AC 2
1
kk
3
=
−= ,
V× gãc gi÷a c¸c ®−êng th¼ng nµy lµ π/4 nªn
1
12
1
12
1
k
kk 3
tg 1
k
41kk 13
+
−
π===
+−
VËy 1
1
1
k31
k
13
+
=
−
vµ 1
1
1
k31
k
13
+
=
−
−
.
Gi¶i ra ta ®−îc : 1
k = 1
2 vµ 1
k = − 2.
VËy mét trong nh÷ng ®−êng th¼ng cÇn t×m cã d¹ng
y − 2 = 1(x 2)
2− ⇔ 2y − x − 2 = 0 ,
cßn ®−êng th¼ng kia lµ
y − 2 = − 2(x − 2) ⇔ 2x + y − 6 = 0.
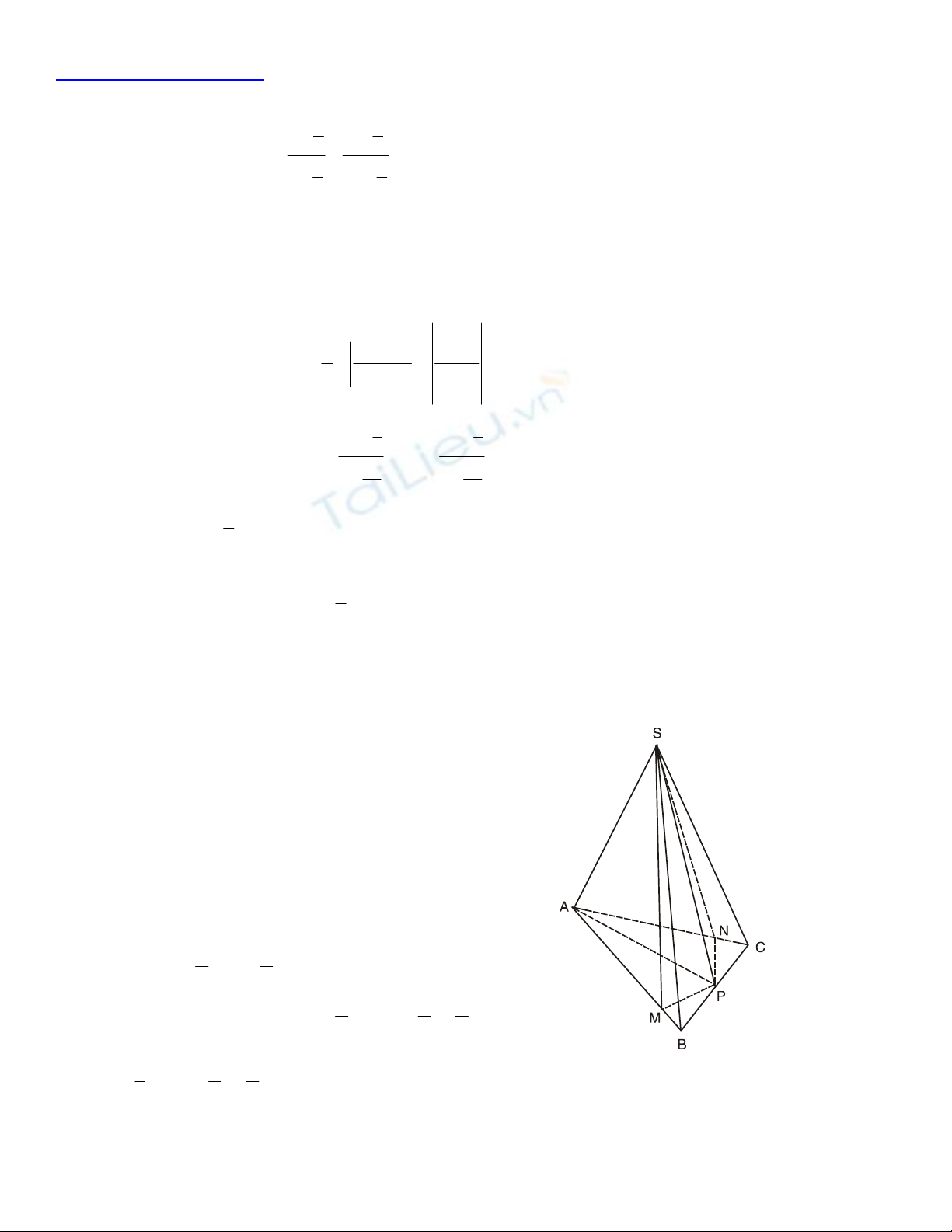
C©u IVb.
1) Tõ AM = AN = AP suy ra SM = SN = SP, vËy SMP vµ SNP
lµ hai tam gi¸c c©n cã cïng c¹nh bªn. DiÖn tÝch cña
chóng b»ng nhau, vËyMP = NP. Tõ kÕt qu¶ nµy suy ra
c¸c tam gi¸c AMP vµ ANP b»ng nhau,
do ®ã AP lµ ph©n gi¸c gãc A, mµ ABC lµ tam gi¸c c©n,
vËy AP còng lµ ®−êng cao vµ trung tuyÕn cña tam gi¸c ®ã,
thµnh thö P lµ trung ®iÓm
cña BC.
2) ABP lµ tam gi¸c vu«ng, vËy
AM = AP = AB cos a cos
22
αα
= ,
dt(AMPN) = 2 dt(AMP) 22
AM.APsin a cos sin
222
ααα
== ,
thµnh thö
22
SAMPN 1
Vhacossin
322
αα
=.
3) (SAP) lµ mÆt ph¼ng ®èi xøng cña h×nh chãp S.AMPN, vËy nÕu I lµ mét ®iÓm thuéc (SAP)
th× kho¶ng c¸ch tõ I ®Õn (SAM) vµ (SAN) lµ b»ng nhau, kho¶ng c¸ch tõ I ®Õn (SMP) vµ (SNP)
lµ b»ng nhau.
www.khoabang.com.vn LuyÖn thi trªn m¹ng – Phiªn b¶n 1.0
________________________________________________________
XÐt giao tuyÕn  cña c¸c mÆt ph¼ng ph©n gi¸c c¸c gãc nhÞ diÖn (A, SM, P) vµ (S, AM, P).
HiÓn nhiªn  kh«ng song song víi (SAP), do ®ã c¾t (SAP) t¹i I. §iÓm I c¸ch ®Òu c¸c mÆt
ph¼ng (SAM), (SPM) vµ (AMP), vËy c¸ch ®Òu tÊt c¶ c¸c mÆt cña h×nh chãp S.AMPN, tøc lµ I
lµ t©m h×nh cÇu néi tiÕp h×nh chãp Êy.
B¸n kÝnh r h×nh cÇu nµy cã thÓ tÝnh ®−îc theo c«ng thøc
1
VSr
3
=,
trong ®ã V, S lÇn l−ît lµ thÓ tÝch vµ diÖn tÝch toµn phÇn h×nh chãp S.AMPN. Ta cã
dt(SAM) = 1
2AM . SA = 1ha cos
22
α
.
§Ó tÝnh diÖn tÝch tam gi¸c c©n SMP, gäi H lµ trung ®iÓm cña MP. V× MP lµ ®¸y cña tam gi¸c c©n
AMP, nªn
MH AMsin asin cos
442
ααα
== ,
AH AM.cos a cos cos
442
ααα
== ,
222222
SH SA AH h a cos cos
42
α
α
=+=+
VËy dt (SMP) = MH . SH =
222 2
asin cos h a cos cos
42 4 2
αα α α
=+ ,
vµ ta ®−îc
S = 2dt(SAM) + 2dt(SMP) + 2dt(AMP) 222 2
2asin cos h a cos cos
42 4 2
α
ααα
=+
+
+ 22
ahcos a cos sin
222
ααα
+.