Số hiệu: BM1/QT-PĐBCL-RĐTV Trang: 1/1
TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT
THÀNH PHỐ HỒ CHÍ MINH
KHOA ĐÀO TẠO CHẤT LƯỢNG CAO
NGÀNH: Công nghệ Kỹ thuật Máy tính
-------------------------
ĐỀ THI CUỐI KỲ HỌC KỲ II
NĂM HỌC 2019-2020
Môn: Cấu Trúc Rời Rạc
Mã môn học: DSCC235864
Đề thi có 01 trang.
Thời gian: 75 phút.
Được phép sử dụng tài liệu.
Câu 1: (1.5 điểm)
a. Cho cc mệnh đề p, q, r. Chứng minh: [¬p → (q → r)] [q → (p ∨ r)].
b. Lấy phủ định của mệnh đề sau (viết cụ thể bằng lời):
“P: Nếu trời mưa và bạn không đến đón thì tôi không đi học.”
c. Hãy kiểm tra suy luận sau:
t→u
r → (s t)
( pq ) → r
(s u )
______________
p
Câu 2: (1 điểm)
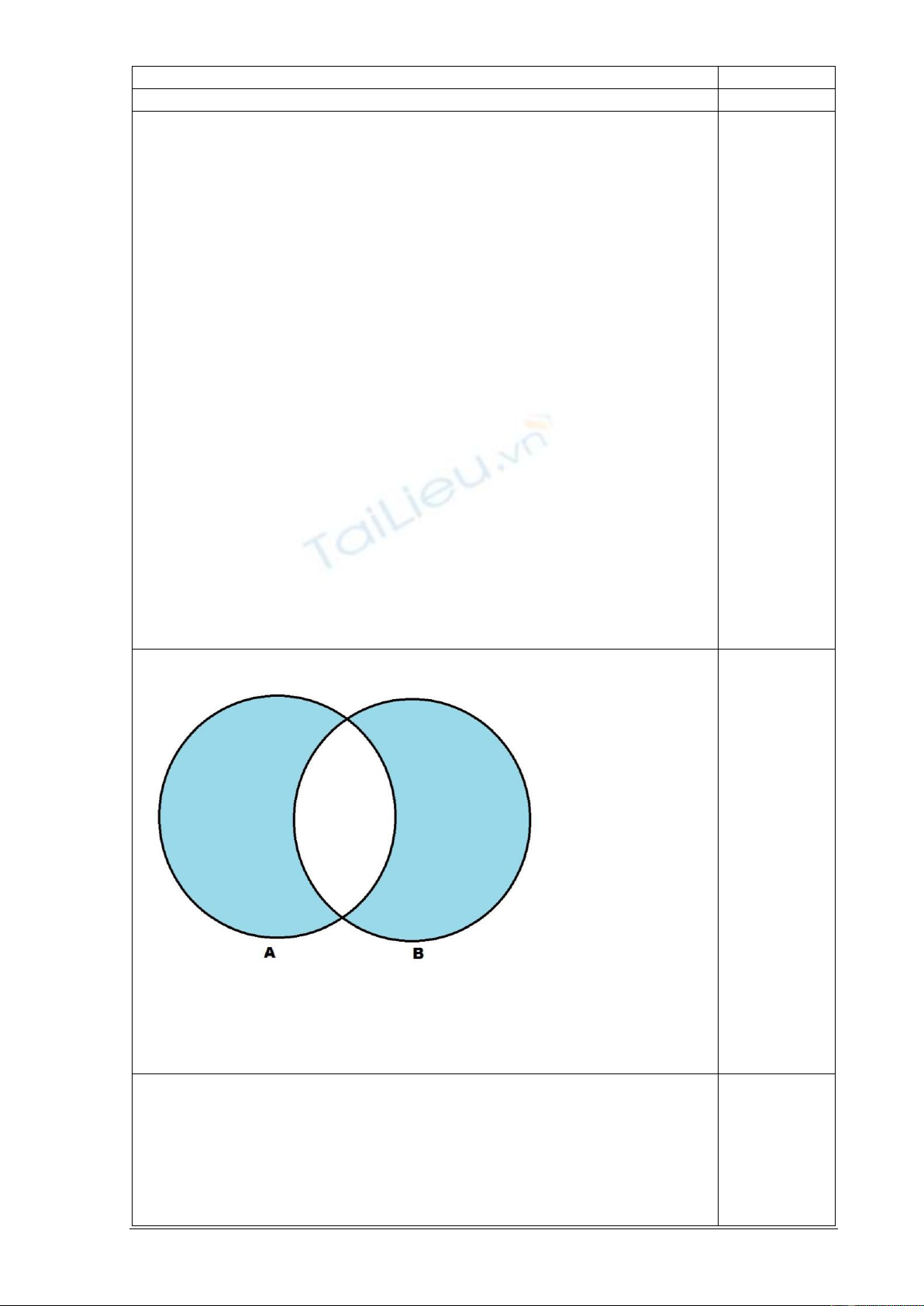
a. Vẽ sơ đồ Venn thể hiện sự kết hợp giữa cc tập hợp A và B như sau: (A−B)∪(B−A). Giả
định rằng 2 tập hợp A và B giao nhau.
b. Cho f là hàm từ R sang R được xc định bởi: f(x)=x2. Tìm f −1({x|x>4}).
Câu 3: (2.5 điểm)
Cho X = {𝑑 ∈ ℕ: 12 𝑐ℎ𝑖𝑎 ℎế𝑡 𝑐ℎ𝑜 𝑑}, và cho R = {(𝑎, 𝑏) ∈ 𝑋 × 𝑋: 𝑏 𝑐ℎ𝑖𝑎 ℎế𝑡 𝑐ℎ𝑜 𝑎}.
a. Chứng minh rằng (X,R) là một tập sắp thứ tự (poset). Lý giải cụ thể từng luận điểm.
b. Vẽ biểu đồ Hasse.
c. Poset trên có phần tử lớn nhất (maximum) và nhỏ nhất (minimum) hay không? Tại sao?
d. Poset trên có phải là một Lattice hay không? Tại sao?
Câu 4: (3.5 điểm)
Cho A = {a, b, c, d, e}, và cho R là một quan hệ trên tập A với ma trận quan hệ như sau:
a
b
c
d
e
a
0
0
1
0
0
b
0
0
0
1
0
c
1
0
0
0
0
d
0
1
0
0
0
e
0
0
0
1
0
a. Hãy biểu diễn R bằng đồ thị có hướng (directed graphs)
b. Quan hệ R có (hoặc không có) cc tính chất nào trong những tính chất sau: phản xạ, đối
xứng, phản đối xứng, bắc cầu? Tại sao?
c. Hãy tìm bao đóng (closure) của R để nó vừa đối xứng vừa phản xạ.
d. Hãy tìm bao đóng (closure) của R để nó vừa phản xạ vừa bắc cầu.
Câu 5: (1.5)
a. Viết mã giả (pseudocode) (hoặc chương trình) cho thuật ton tìm số nguyên nhỏ nhất
trong một mảng gồm n số nguyên bằng cch so snh mỗi số nguyên với số nhỏ nhất đã tìm
được trước đó.
b. Tính số phép so snh phải thực hiện trong trường hợp tốt nhất (best-case) và xấu nhất
(worst-case) của thuật ton trên. Lý giải cụ thể kết quả đạt được.
c. Kết luận về độ phức tạp tính toán (time complexity) (big-O) cho cc trường hợp tốt và
xấu nhất.
Ghi chú: Cán bộ coi thi không được giải thích đề thi.
Số hiệu: BM1/QT-PĐBCL-RĐTV Trang: 1/1
Chuẩn đầu ra của học phần (về kiến thức)
[CĐR 1.1]: Có khả năng đếm cc bộ khc nhau của cc
đối tượng rời rạc bằng cch sử dụng cc kỹ thuật liệt kê
cơ bản.
[CĐR 1.2]: Có khả năng tạo ra cc công thức liệt kê họ
cc đối tượng sử dụng lý thuyết tập hợp, đệ quy và cc
hàm khởi tạo.
[CĐR 1.3]: Có thể giải quyết cc loại vấn đề khc nhau
trên cc đồ thị rời rạc.
[CĐR 1.4]: Có thể thực thi cc thuật ton cho nhiều loại
vấn đề khc nhau trên cc đồ thị rời rạc.
[CĐR 1.5]: Có khả năng chứng minh cc kết quả khc
nhau trong lý thuyết liệt kê hoặc lý thuyết đồ thị bằng
cch sử dụng quy nạp, bộ đếm, lý thuyết tập hợp qua cc
đối số song nh và phủ định.
Ngày 06 tháng 07 năm 2020
Thông qua Trưởng ngành
(ký và ghi rõ họ tên)
Số hiệu: BM1/QT-PĐBCL-RĐTV Trang: 1/1
Đp án
Điểm
Câu 1:
1.5
a. (0) ¬p → (q → r)
(1) p ∨ ¬q ∨ r (Implication)
(2) ¬q ∨ p ∨ r (Associative)
(3) q → (p ∨ r) (Implication)
b. Mệnh đề phủ định của mệnh đề đã cho: ((p q) → r) = p q r
“𝑃
: Trời mưa và bạn không đến đón mà tôi vn đi học.”
c.
t→ u (1)
r → (s t) (2)
( pq ) → r (3)
(s u ) (4)
s  u (5) ((4) + De Morgan)
u (6) (Simplification)
t (7) ((1)+(6) + Negation)
s (8) ((5) + Simplification)
t s (9) ((7)+(8)+ Conjunction)
(t s) (10) ((9)+De Morgan)
r (11) ((2)+(10)+ Modus tollens)
(pq) (12) ((3)+(11)+ Modus tollens)
pq (13) ((12) + Negation)
p (14) ((13)+Simplification)
0.5
0.5
0.5
Câu 2:
a.
b. f −1({x|x>4}) chứa tất cả cc phần tử thuộc tập hợp R, và có cc ảnh như
là một số thực lớn hơn 4.
Do đó ta có: f(x) >4 → x2 >4 → x<-2 hoặc x >2.
f −1({x|x>4}) = {x|(x<-2)v(x>2)}
0.5
0.5
Câu 3:
a. Cho a∈X ta có a chia hết cho chính bản thân nó. Do đó aRa đúng, (X,R)
có tính phản xạ.
Cho a,b∈X ta có b chia hết cho a (aRb) và a cũng chia hết cho b (bRa)
khi và chỉ khi a=b. Do đó (X,R) có tính phản đối xứng.
Cho a,b,c∈X ta có b chia hết cho a (aRb) và c chia hết cho b (bRc) nên c
cũng chia hết cho a (aRc). Do đó (X,R) có tính bắc cầu.
0.25
0.25
0.25
Số hiệu: BM1/QT-PĐBCL-RĐTV Trang: 1/1
Từ cc dữ kiện trên ta có thể suy ra (X,R) là một tập sắp thứ tự (poset).
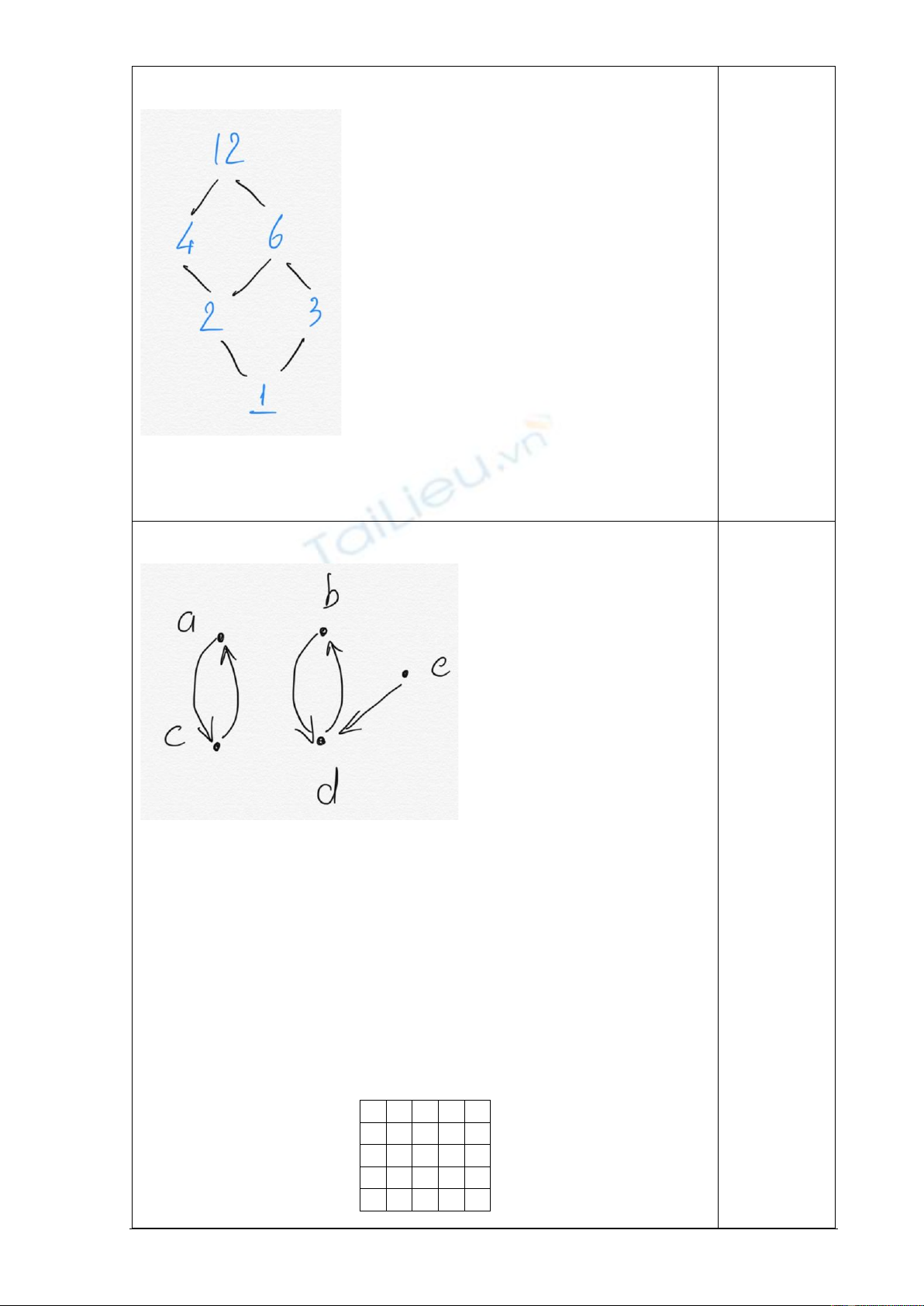
b. Biểu đồ Hasse:
c. Poset có một phần tử cực đại duy nhất là 12 và một phần tử cực tiểu duy
nhất là 1 do đó nó có phần tử lớn nhất (12) và phần tử nhỏ nhất (1).
d. Poset này là một Lattice vì mỗi cặp trong poset đều có chặn trên nhỏ nhất
và chặn dưới lớn nhất.
0.25
0.5
0.5
0.5
Câu 4:
a. Đồ thị có hướng:
b. Xét cc tính chất: phản xạ, đối xứng, phản đối xứng và bắc cầu.
- Không có tính phản xạ vì tất cả cc phần tử tại đường chéo chính đều bằng
0.
- Không có tính đối xứng vì có eRd nhưng không có dRe.
- Không có tính phản đối xứng vì có aRc và cRa nhưng a≠c.
- Không có tính bắc cầu vì có eRd và dRb nhưng không có eRb.
c. Tìm bao đóng của R để nó vừa phản xạ vừa đối xứng.
Bao đóng để R phản xạ: R∪ ∆, với ∆={(a,a), (b,b), (c,c), (d,d), (e,e)}
Bao đóng để R đối xứng: R∪R’, với R’ = {(d,e)}.
Vậy bao đóng để R vừa phản xạ vừa đối xứng là: R∪ ∆ ∪R’
d. Tìm bao đóng của R để nó vừa phản xạ vừa bắc cầu.
Bao đóng để R có tính chất phản xạ:
1
0
1
0
0
0
1
0
1
0
1
0
1
0
0
0
1
0
1
0
0
0
0
1
1
0.5
0.5
0.5
0.5
0.5
0.5
Số hiệu: BM1/QT-PĐBCL-RĐTV Trang: 1/1
Sử dụng giải thuật Warshall trên ma trận này ta có:
1
0
1
0
0
0
1
0
1
0
W0 =
1
0
1
0
0
0
1
0
1
0
0
0
0
1
1
W3 = W2 = W1 = W0
1
0
1
0
0
0
1
0
1
0
W4 =
1
0
1
0
0
0
1
0
1
0
0
1
0
1
1
W5 = W4
Bao đóng để R vừa có tính chất phản xạ vừa có tính chất bắc cầu là W4.
0.5
Câu 5:
a.
procedure minimum (a1, a2, a3, … an: natural numbers with n > 1)
min:= a1
for i:= 2 to n
if ai <min then min:=ai
return min
b. Chúng ta luôn phải thực hiện 1 phép so snh (ai<min) cho mỗi vòng lặp
for. Và vì i có thể nhận được n-1 gi trị (từ 2 đến n), do đó chúng ta chỉ có n-
1 vòng lặp for. Chính vì lẽ đó chúng ta luôn phải sử dụng n-1 phép so sánh
khi đầu vào của thuật ton chứa n số nguyên dù là trong trường hợp tốt nhất
hay xấu nhất.
c. Vì n-1 có big-O là O(n), do đó độ phức tạp tính ton trong trường hợp tốt
nhất hay xấu nhất đều là O(n).
0.5
0.75
0.25