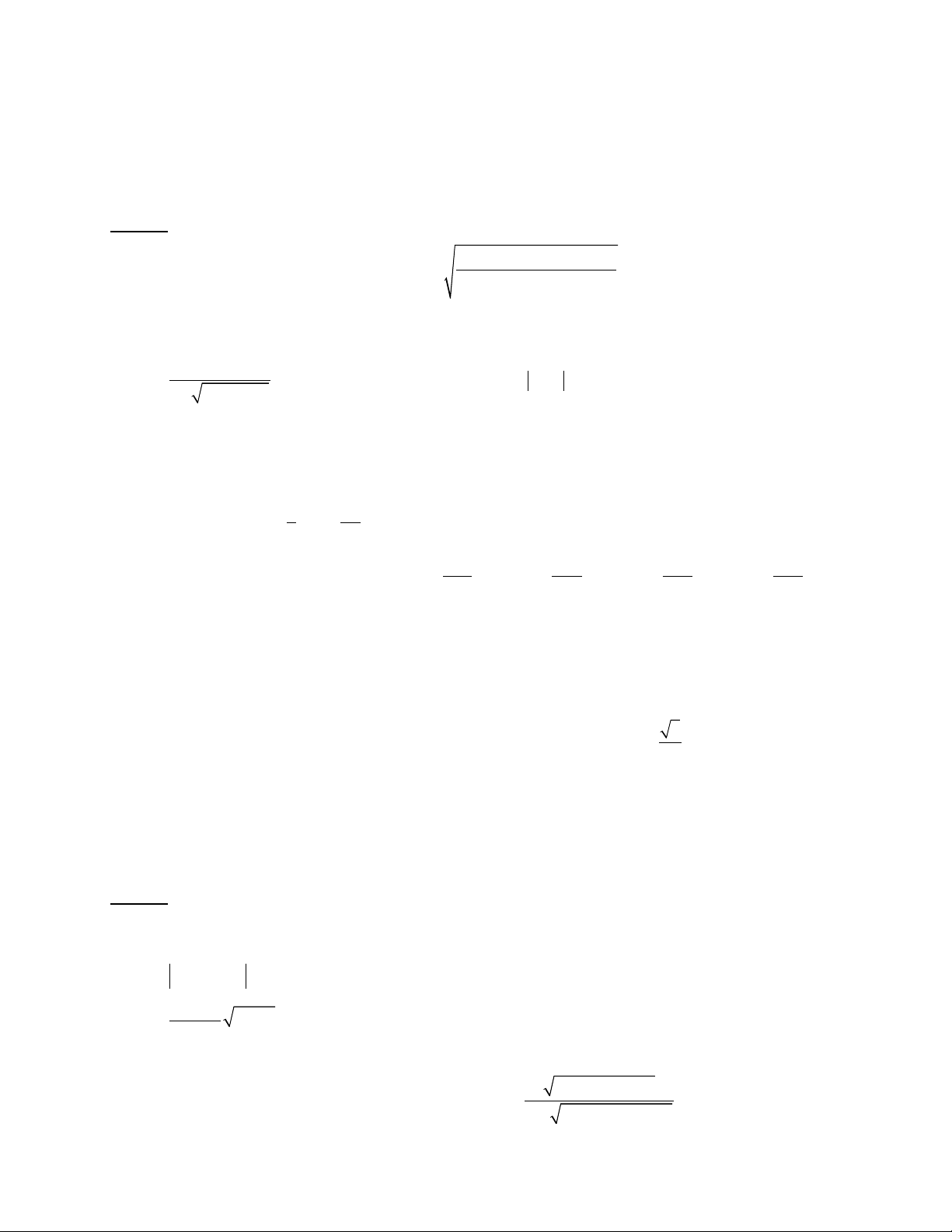
S GIÁO D C VÀ ĐÀO T O HÀ N IỞ Ụ Ạ Ộ
TR NG THPT CHU VĂN ANƯỜ
__________________
Đ C NG ÔN T P H C KÌ IIỀ ƯƠ Ậ Ọ
NĂM H C 2018-2019Ọ
Môn: Toán
Kh i l p:10 - Ch ng trình: C B Nố ớ ươ Ơ Ả
Đ 01Ề
Bài 1 (1 đi mể). Tìm t p xác đnh hàm s ậ ị ố
( )
( )
2
2
3 2 .
5 5 2012
x x
yx x x
− +
=− − +
Bài 2 (3,5 đi mể).
1. Gi i các b t ph ng trình sau ả ấ ươ
a)
2
2
3 2 5 0;
1 2
x x
x x
− + +
− + +
b)
2
3 2 3.x x x− > − − +
2. Xác đnh giá tr tham s ị ị ố
m
đ h b t ph ng trình ể ệ ấ ươ
( )
2
4 3 0
2 3 1
x x
mx m m x
− +
− + > +
vô nghi mệ
Bài 3 (2 đi mể).
1. Cho bi t ế
1 3
os , ;2 .
3 2
c
π
α α π
=
Tính các giá tr l ng giác còn l i c a góc ị ượ ạ ủ
.
α
2. Rút g n bi u th c ọ ể ứ
16 22 28 34
sin sin sin sin sin .
5 5 5 5
M x x x x x
π π π π
= + + + + + + + +
Bài 4 (3 đi mể).
Trong m t ph ng to đ ặ ẳ ạ ộ
cho đng th ng ườ ẳ
1
1 2
:1
x t
dy t
= −
= − +
và đng th ng ườ ẳ
2
: 2 3 0.d x y− + =
1. Xét v trí t ng đi c a ị ươ ố ủ
1 2
, .d d
2. Xác đnh v trí đi m ị ị ể
1
M d
sao cho kho ng cách t ả ừ
M
đn ế
2
d
b ng ằ
5.
5
3. L p ph ng trình đng tròn đi qua ậ ươ ườ
O
và ti p xúc hai đng th ng ế ườ ẳ
1 2
, .d d
Bài 5 (0,5 đi mể). Cho
,x y
là các s th c tho mãn : ố ự ả
2 2
2 1.x xy y− + =
Tìm giá tr l n nh t, giá tr nh nh tị ớ ấ ị ỏ ấ
c a bi u th c ủ ể ứ
2 2
.M x xy y= − +
Đ 02Ề
Bài 1(2,5 đi mể). Gi i các b t ph ng trình sauả ấ ươ
1.
2
3 2 2x x x− + −
2.
2
2
29 0.
1
x x x
x
−−
+
Bài 2 (2 đi mể).
1. Tìm các giá tr c a tham s ị ủ ố
m
sao cho hàm s ố
2
2
2 1
2 2 2 5
x x m
y
x x m
+ + −
=− − + −
xác đnh trên ị
.?
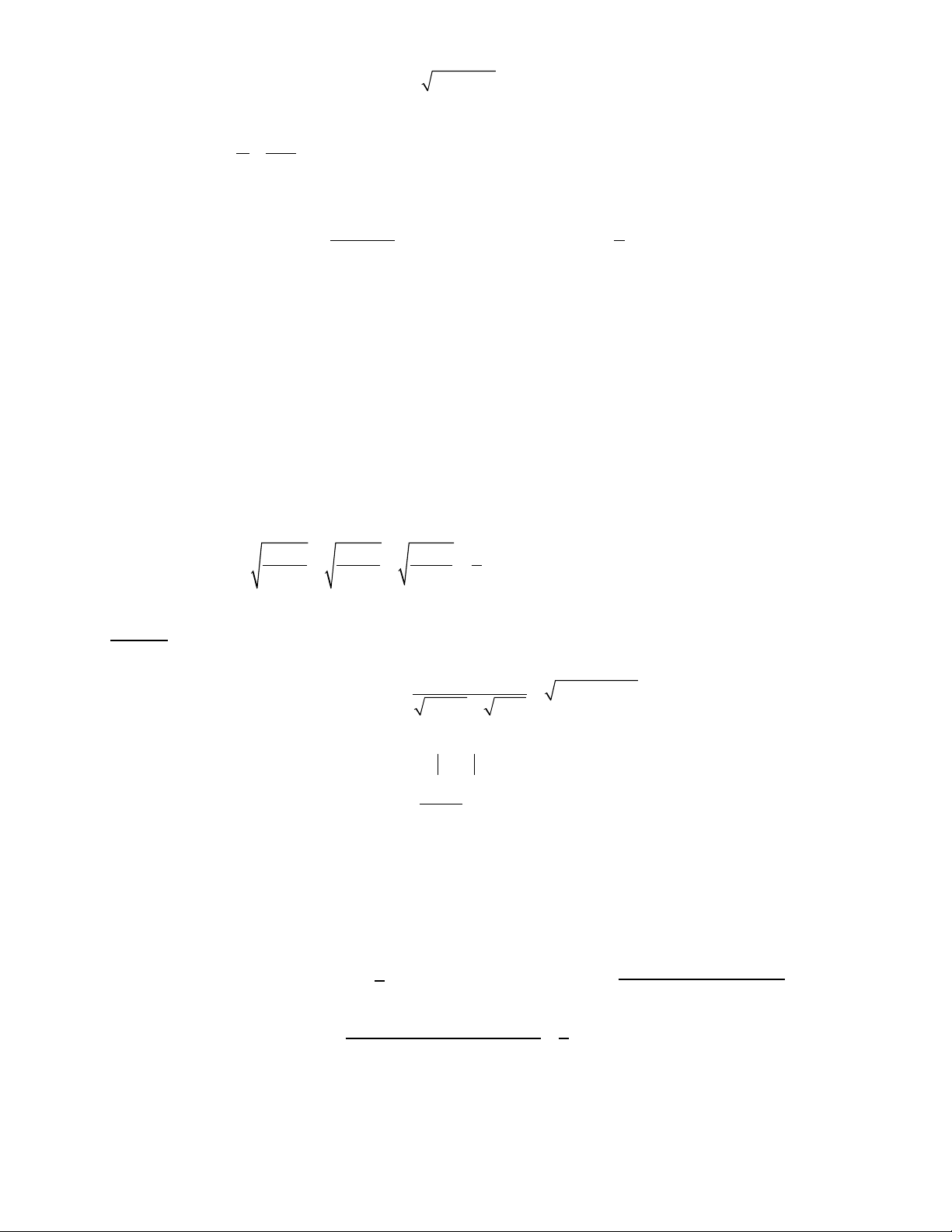
2. Gi i b t ph ng trình ả ấ ươ
( )
22
2 1 3 1 6 0.x x x+ − + − −
Bài 3 (1,5 đi mể).
1. Tính
2
sin , .
6 3 ?
kk
π π
+
2. Ch ng minh đng th c sau không ph thu c vào ứ ẳ ứ ụ ộ
α
( )
3
2 4 6 2
2
1 3
3 os 3sin sin sin 2 .
1 cot 4
M c
α α α α
α
= + + − +
+
Bài 4 (3,5 đi mể).
1. Trong m t ph ng to đ ặ ẳ ạ ộ
cho h đng congọ ườ
( ) ( )
2 2
: 2 2 1 6 8 0.
m
C x y mx m y m+ + − + − − =
Ch ng t r ng h ứ ỏ ằ ọ
( )
m
C
là h các đng tròn. Xác đnh tâm và bán kính đng tròn có bán kính nh nh t ọ ườ ị ườ ỏ ấ
trong h ọ
( )
.
m
C
2. Trong m t ph ng to đ ặ ẳ ạ ộ
cho tam giác
ABC
có
?
0
90 ,A=
: 2 0,AB x y− + =
đng caoườ
: 3 8 0.AH x y− + =
Đi m ể
( )
7; 11M−
thu c đng th ng ộ ườ ẳ
.BC
a) Xác đnh to đ các đnh tam giác ị ạ ộ ỉ
.ABC
Tính di n tích tam giác ệ
.ABC
b) Xác đnh ph ng trình đng tròn ngo i ti p tam giác ị ươ ườ ạ ế
.ABC
Bài 5 (0,5 đi mể). Cho
, , 0x y z >
tho mãn ả
3 .xy yz zx xyz+ + =
Ch ng minh r ng ứ ằ
1 1 1 3 .
3 3 3 2x y y z z x
+ +
+ + +
Đ 03Ề
Bài 1 (1,5 đi mể). Gi i b t ph ng trình ả ấ ươ
2
22 5 3 1.
2 3 1
xx x
x x
+ + + +
+ − +
Bài 2 (2,5 đi mể).
1. Gi i h b t ph ng trình ả ệ ấ ươ
( )
( )
3 2 1 0
10.
3 2
x x
x
x
− − −
−>
+
2. Cho hàm s ố
( ) ( ) ( )
2
2 2 2 2 4.f x m x m x m= + − + − +
(
m
là tham s )ố
a) Xác đnh ị
m
sao cho
( )
1 4f x m − −
v i m i ớ ọ
.?x
b) Xác đnh ị
m
sao cho b t ph ng trìnhấ ươ
( )
0f x
vô nghi m. ệ
Bài 3 (2 đi mể).
1. Cho góc
α
tho mãn ả
2
tan .
3
α
=
Tính giá tr c a bi u th c ị ủ ể ứ
( )
( )
2sin 2010 cos .
3cos 2011 sin
x x
Mx x
π
π
+ −
=− +
2. Ch ng minh đng th c ứ ẳ ứ
( )
( )
2
4
sin 2 2 cos 3 2 2 1cot .
3 4cos 2 os 4 2c x
α π α α
α π
+ + − =
− + + −
Bài 4 (3,5 đi mể). Trong m t ph ng to đ ặ ẳ ạ ộ
cho đng tròn ườ
( )
C
có ph ng trình ươ
2 2
4 5 0x y x+ − − =
và đi m ể
( )
1;4 .M−
1. Ch ng t ứ ỏ
M
n m ngoài đng tròn. L p ph ng trình ti p tuy n v i đng tròn bi t ti p tuy n ằ ườ ậ ươ ế ế ớ ườ ế ế ế
đi qua đi m ể
.M
2. L p ph ng trình đng tròn đi x ng đng tròn ậ ươ ườ ố ứ ườ
( )
C
qua đng th ng ườ ẳ
: 2 3 0.d x y− + =
3. Tính di n tích tam giác đu ệ ề
ABC
n i ti p đng tròn ộ ế ườ
( )
.C
4. L p ph ng trình đng th ng đi qua đi m ậ ươ ườ ẳ ể
( )
1;0A−
và c t đng tròn ắ ườ
( )
C
t i hai đi m phân bi tạ ể ệ
sao cho
4.EF =
Bài 5 (0,5 đi mể). Tìm các giá tr ị
0x
th a mãn b t ph ng trình: ỏ ấ ươ
2 3 2
4 6 3 2 .x x x x x− − > + +
Đ 04Ề
Bài 1(2,5 đi mể). Cho b t ph ng trình ấ ươ
( ) ( ) ( )
2
1 2 3 6 0, 1 .x x x x m+ − − − + + +
(
m
là tham s )ố
1. Gi i b t ph ng trình (1) v i ả ấ ươ ớ
0.m=
2. Xác đnh ị
m
sao cho b t ph ng trình ấ ươ
( )
1
nghi m đúng v i m i ệ ớ ọ
[ ]
2;3 .x −
Bài 2 (2,5 đi mể).
1. Gi i b t ph ng trình ả ấ ươ
2
21.
3 4
x x
x
−
−
2. Xác đnh ị
m
sao cho h b t phu ng trình ệ ấ ơ
( )
2
2 3
1 2 1
x x
m x m
− +
+ −
có nghi m duy nh t.ệ ấ
Bài 3 (1,5 đi mể).
1. Cho tam giác
.ABC
Ch ng minh r ng ứ ằ
222
sin sin sin 2sin .sin .cos .A B C A B C+ − =
2. Ch ng minh r ngứ ằ
( )
1
) sin .sin .sin sin 3 ;
3 3 4
) sin 5 2sin cos 4 cos 2 sin .
a
b
π π
α α α α
α α α α α
− + =
− + =
Bài 4 (3 đi mể). Trong m t ph ng to đ ặ ẳ ạ ộ
cho hình bình hành
ABCD
,đnh ỉ
( )
1; 2 ,A−
4
: ,
4 2 ?
x t
BD t
y t
= +
= − −
và
133 58
;
37 37
H
−
là hình chi u c a ế ủ
A
trên
.DC
1. L p ph ng trình các đng th ng ậ ươ ườ ẳ
, .DC AB
2. Xác đnh to đ các đnh ị ạ ộ ỉ
, , .D C B
3. Xác đnh v trí đi m ị ị ể
M BD
sao cho
2 2 2 2
MA MB MC MD+ + +
đt giá tr bé nh t .ạ ị ấ
Bài 5.(0,5 đi mể). Tìm giá tr nh nh t c a hàm s ị ỏ ấ ủ ố
2
5
2 , 2.
1
y x x
x
= +
+
Đ 05Ề
Bài 1 (1,5 đi mể). Gi i h b t ph ng trình ả ệ ấ ươ
( )
2
2 2 1 8 4
3 2 3
x x x
x x
− − −
− +
Bài 2 (3 đi mể).
1. Gi i b t ph ng trình ả ấ ươ
( )
2
3 4 5 6 0.
4
x x x
x
− + +
−
2. Xác đnh ị
m
đ m i ể ọ
[
)
2;x +
đu là nghi m c a b t ph ng trình ề ệ ủ ấ ươ
( )
1 5 1 5 1 .m x x m− − − +
Bài 3 (1,5 đi mể).
1. Cho bi t ế
1
cot .
4
α
=
Tính giá tr bi u th c ị ể ứ
3
3
sin os .
cos sin
c
A
α α
α α
+
=+
2. Rút g n bi u th c ọ ể ứ
( )
( ) ( ) ( ) ( )
( )
0 0 0 0
0 0
cos 90 tan 180 cos 180 sin 270 .
sin 180 tan 270
B
α α α α
α α
− − + +
= +
− +
Bài 4 (3,5 đi mể). Trong m t ph ng to đ ặ ẳ ạ ộ
cho các đng th ng ườ ẳ
1 2
1
: , : 2 3 5 0
2
x t
d d x y
y t
= −
− + =
= +
và
đi m ể
( )
0;1 .M
1. Xác đnh to đ đi m ị ạ ộ ể
( )
1
;E x y d
sao cho
2 2
E E
x y+
đt giá tr bé nh t.ạ ị ấ
2. Vi t ph ng trình đng th ng ế ươ ườ ẳ
3
d
đi x ng ố ứ
1
d
qua
2
.d
3. Vi t ph ng trình đng th ng ế ươ ườ ẳ
∆
c t ắ
1 2
,d d
t i ạ
,A B
sao cho tam giác
MAB
vuông cân t i ạ
.M
4. L p ph ng trình đng tròn ậ ươ ườ
( )
C
có tâm
M
và c t đng th ng ắ ườ ẳ
2
d
t i hai đi m phân bi t ạ ể ệ
,P Q
sao
cho di n tích tam giác ệ
MPQ
b ng ằ
6
13
.
Bài 5 (0,5đi mể). Tam giác
ABC
có đc đi m gì n u ặ ể ế
( )
2
3.
36
S a b c= + +
(V i ớ
, ,abc
là 3 c nh tam giác vàạ
S
là di n tích tam giác ệ
).ABC
Đ 06Ề
Bài 1.(1,5 đi mể) Cho
( ) ( ) ( )
2
1 2 1 3f x m x m x m
= + − − +
,
m
là tham s .ố
1.Xác đnh giá tr ị ị
m
sao cho
( )
3f x
đúng v i m i ớ ọ
x?
.
2. Xác đnh giá tr ị ị
m
sao cho ph ng trình ươ
( )
2f x
= −
có hai nghi m trái d u.ệ ấ
Bài 2.(3 đi m) Gi i b t ph ng trình sauể ả ấ ươ
1.
2
4 3 2 1x x x
+ − > −
2.
2 2
3 5 7 3 5 2 1x x x x
+ + − + +
.
Bài 3.(1,5đi mể)
1.Cho bi t ế
3
sin os 5
c
α α
+ =
. Tính giá tr bi u th c ị ể ứ
os4c
α
.
2.Ch ng minh r ng: ứ ằ
ABC
∆
vuông n u ế
sin sin
sin cos cos
B C
AB C
+
=+
.
Bài 4 (3,5 đi mể). Trong m t ph ng to đ ặ ẳ ạ ộ
xOy
,cho
( )
2 2
: 1
9 4
x y
E
+ =
1. Xác đnh các tiêu đi m,tiêu c ị ể ự
( )
E
,tâm sai,to đ các đnh,đ dài các tr c c a ạ ộ ỉ ộ ụ ủ
( )
E
.V (E).ẽ
2. Xác đnh v trí đi m ị ị ể
( )
M E
bi t ế
1 2
2 0MF MF− =
3. Tìm đi m ể
( )
H E
bi t ế
?
1 2
90F HF =
o
.
Bài 5.(0,5 đi mể). Tìm giá tr tham s ị ố
m
sao cho b t ph ng trình ấ ươ
2 2
6 2 1x x m x mx m
+ + − − −
nghi m đúng v i m i ệ ớ ọ
x?
.
-------------------------------H T-------------------------------Ế