TRƯỜNG THPT NGUYỄN HUỆ
BỘ MÔN : TOÁN
GIÁO VIÊN ĐẶNG VĂN HIỂN
KIỂM TRA CHẤT LƯỢNG HỌC KỲ I
Năm học: 2013-2014
Môn thi: TOÁN- Lớp 12
Thời gian: 90 phút (không kể thời gian phát đề)
ĐỀ SỐ 01
(Đề gồm có 01 trang)
I. PHẦN CHUNG (7,0 điểm)
Câu I ( 3 điểm)
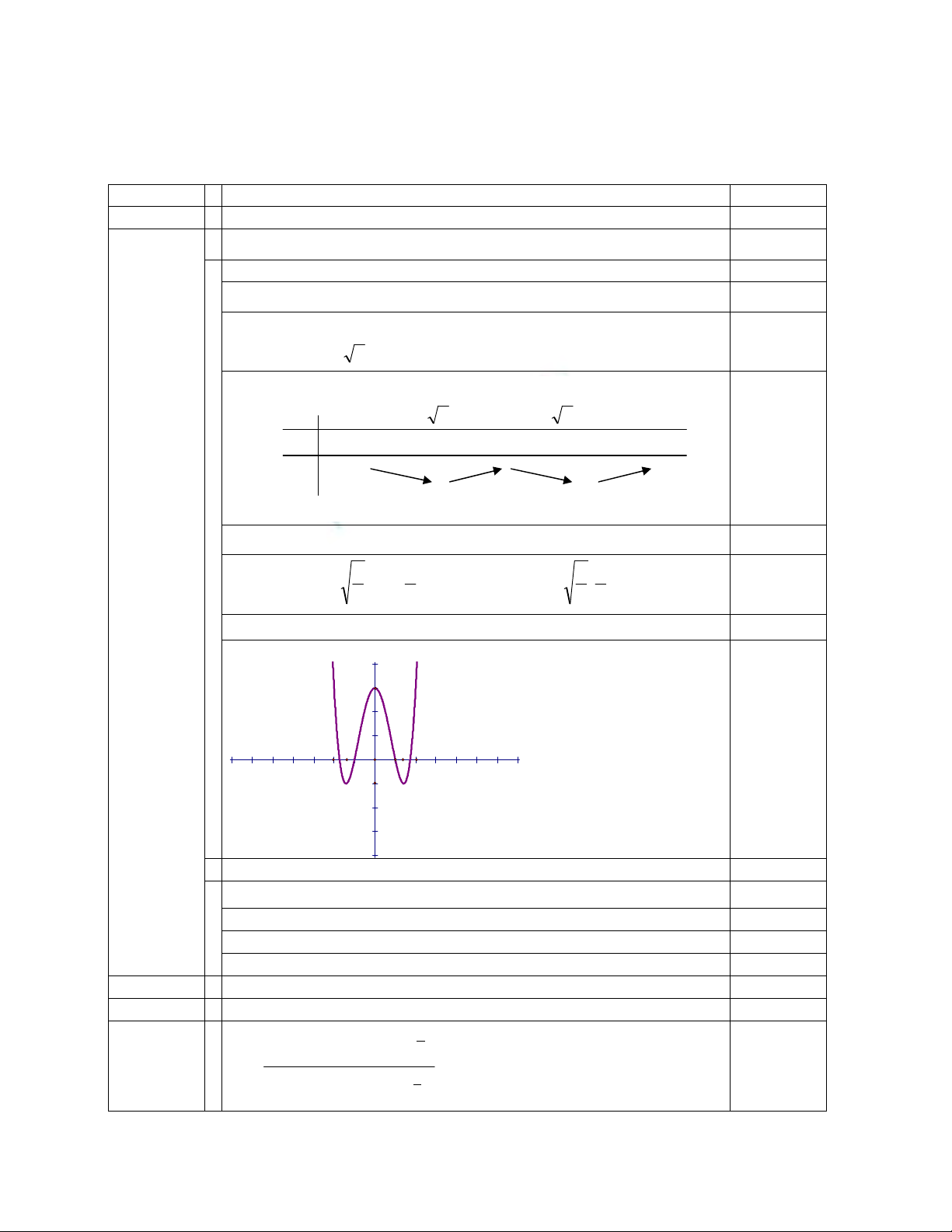
Cho hàm số 34 24 xxy , gọi đồ thị của hàm số là (C) .
1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho .
2. Dựa vào đồ thị (C) , tìm tất cả các giá trị của m để phương trình
022 2
2 mx có 4
nghiệm phân biệt.
Câu II ( 3 điểm)
1. Tính giá trị của biểu thức 98log14log
75log405log
22
33
Q .
2. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2x x
y e 4e 3
= - +
trên [0;ln4]
Câu III ( 1 điểm)
Cho hình trụ có đáy là hình tròn ngoại tiếp hình vuông cạnh a . Diện tích của thiết diện qua
trục hình trụ là 2
2a . Tính diện tích xung quanh hình trụ và thể tích khối trụ đã cho .
II. PHẦN RIÊNG (3,0 điểm)
(Học sinh chọn IVa và Va hay IVb và Vb )
A. Thí sinh ban nâng cao
Câu IVa ( 1 điểm)
Tìm m để tiệm cận xiên của đồ thị hàm số 2
x mx 1
y
x 1
+ -
=
-
(m
¹
0) đi qua gốc toạ độ .
Câu Va ( 2 điểm)
Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a . Cạnh bên của lăng trụ
hợp với đáy góc 600 . Đỉnh A’ cách đều A,B,C .
1. Chứng minh tứ giác BB’C’C là hình chữ nhật .
2. Tính thể tích khối lăng trụ ABC.A’B’C’ .
B. Thí sinh ban cơ bản
Câu IVb ( 1 điểm)
Giải bất phương trình : 0833 2 xx .
Câu Vb ( 2 điểm)
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy là a . Tam giác SAC là tam giác đều .
1) Tính độ dài đường cao của chóp SABCD .
2) Tính thể tích khối chóp S.ABCD .
.........Hết.......
HƯỚNG DẪN CHẤM ĐỀ SỐ 01
(Hướng dẫn chấm gồm có…03 trang)
CÂU
ĐÁP ÁN ĐIỂM
Câu I
3 điểm
1
Khảo sát sự biến thiên và vẽ đồ thị hàm số 34 24 xxy 2,5 điểm
TXĐ : D = R 0,25
xxy 84' 3 0,25
1;2
3;0
0' yx
yx
y 0,25
BBT
0,75
812'' 2 xy 0,25
9
7
;
3
2
0'' yxy . Điểm uốn
9
7
;
3
2
2,1
I 0,25
Điểm khác : 3;2
yx
Đồ thị
4
2
-
2
-
4
-5 5
O 2
-2
3
-1
0,5
2
0,5 điểm
Phương trình viết thành : 1234 24 mxx 0,25
Số nghiệm phương trình là số giao điểm (C) và (d):y = - 2m -1
Do đó ,phương trình có 4 nghiệm phân biệt
023121
mm 0,25
Câu II
3 điểm
1
1,5 điểm
)2.7(log)2.7(log
)3.5(log)3.5(log
2
1
22
2
1
3
4
3
Q
0,5
x
2 0 2
y’ - 0 + 0 - 0 +
3
y -1 -1
2
1
3
2
1
4
3
2.7
2.7
log
3.5
3.5
log
Q
0,5
2
1
2
2
7
3
2log
3log
Q
0,25
Vậy Q = 7 0,25
2
1,5 điểm
Đặt x
et . Do
4ln;0x nên
4;1t 0,25
Hàm số thành 34)( 2 tttg 0,25
g’(t) = 2t -4
4;120)(' ttg 0,25
Có g(1) = 0 ; g(2) = -1 ; g(4) = 3 0,25
Vậy
4ln3
4ln;1 xMaxy 0,25
2ln1
4ln;1
xMiny 0,25
Câu III
1 điểm
O
O'
DC
AB
2aAB nên bán kính đáy hình trụ
2
2a
R 0,25
ha
a
a
BCaSABCD 2
2
2
22
2 0,25
Diên tích xung quanh hình trụ 2
.22 aRhS
0,25
Thể tích khối trụ
2
2
3
2a
hRV
0,25
Câu IVa
1 điểm
m
f(x) x m 1
x 1
= + + +
-
0,25
Ta có x x
)
m
lim f(x) (x m 1) lim 0(m 0
x 1
® ± ¥ ® ± ¥
é ù
ë û
- + + = = ¹
-
0,25
Nên ta có tiêm cận xiện d : y = x + m + 1 0,25
d qua gốc O khi 0 = 0 + m + 1
Þ
m = - 1 0,25
Câu Va
2 điểm
1
1 điểm
C
B
A'
C
'
B'
H
Kẻ A’H
(ABC) tại H . H là tâm đường tròn ngoại tiếp ABC
0,25
Hình chiếu của SC lên (ABC) là AH nên góc A’AH là 60
0
0,25
Có BC
AH nên BC
AA’. Vậy BC
BB’ 0,25
Vây BCC’B’ là hình chữ nhật 0,25
2
1 điểm
Tam giác ABC đều nên
3
3
2
3
3
2aa
AH 0,25
a
a
AHHAHAA 3.
3
3
60tan.':' 0 0,25
Diện tích tam giác ABC là
4
3
2
a 0,25
Thể tích khối lăng trụ
4
3
4
3
'. 32 a
a
a
HASV ABC 0,25
Câu IVb
1 điểm
Đặt 03 x
t 0,25
Bất phương trình thành : 098
2 tt ( do t >0) 0,25
Giải được
t 1hayt 9
> < -
0,25
Giao điều kiện t > 0 được t > 1
Thế lại : 013 x
x là nghiệm bất phương trình 0,25
Câu Vb
2 điểm
H
B
S
D
C
1
Kẻ SH
(ABCD) tại H . H là tâm đường tròn ngoại tiếp ABCD 0,25
Tam giác SAC đều có cạnh 2aAC 0,25
SH là đường cao tam giác đều SAC nên
2
6
2
3
.2 a
aSH
0,5
2
Thể tích khối chóp
ABC
3
2
1
V S .SH
3
1 a 6 a 6
a .
3 2 6
=
= =
0,5
0,5