TRƯỜNG THPT NGUYỄN HUỆ
BỘ MÔN : TOÁN
GIÁO VIÊN ĐẶNG VĂN HIỂN
KIỂM TRA CHẤT LƯỢNG HỌC KỲ I
Năm học: 2013-2014
Môn thi: TOÁN- Lớp 12
Thời gian: 90 phút (không kể thời gian phát đề)
ĐỀ SỐ 12
(Đề gồm có 01 trang)
I.PHẦN CHUNG (7,0 điểm)
Câu I. (3,0 điểm): Cho hàm số
2 1
1
x
y
x
1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
2.Tìm m để đường thẳng d:
y x m
cắt (C) tại 2 điểm phân biệt.
Câu II ( 2,0 điểm)
1.Tính giá trị biểu thức
1 log 3
53
log . . . 8
a
A a a a a
(
0 1
a
)
2.Tìm GTLN và GTNN của hàm số 2
cos cos 2
y x x
Câu III (1,0 điểm): Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a.
SA
vuông
góc với mặt đáy và SA=2a.
1.Tính thể tích khối chóp S.BCD theo a.
2.Tính thể tích khối cầu ngoại tiếp hình chóp S.ABCD
II. PHẦN RIÊNG (3,0 điểm) (Học sinh chọn IVa và Va hay IVb và Vb )
A. Theo chương trình chuẩn.
Câu IVa ( 1 điểm)
Cho hàm số
2 1
1
x
y
x
(C) .Viết pttt của đths(C) tại điểm có hoành độ bằng -2
Câu Va ( 2 điểm)
1.Giải phương trình :
49 10.7 21 0
x x
2.Giải bất phương trình:
2 2
2 2
log 5 3log
x x
.
B. Theo chương trình nâng cao.
Câu IVb ( 1 điểm)Cho hàm số 32
2 3 1
3
x
y x x
có đồ thị (C). Viết phương trình tiếp tuyến
với (C) biết tiếp tuyến có hệ số góc k = 3
Câu Vb ( 2 điểm)
1.Cho hàm số
.sin
x
y e x
.Tính
2
2 ''
1
4
y y
theo x
2.Cho hàm số 2
3
1
x x
y
x
(C). Tìm trên (C) các điểm cách đều hai trục tọa độ.
.........Hết.......
HƯỚNG DẪN CHẤM ĐỀ SỐ 12
(Hướng dẫn chấm gồm có 4 trang)
Câu Nội dung yêu cầu Điểm
1 1.Khảo sát sự biến thiên và vẽ đồ thị của hàm số
2 1
1
x
y
x
( C)
Tập xác định:
\ 1
D
Ta có:
'2
3
0 x D
1
yx
lim 2 ; lim 2
x x
y y
 
=> đường thẳng
2
y
là tiệm cận ngang
1 1
lim ;lim
x x
y y
 
=> đường thẳng
1
x
là tiệm cận đứng của (C)
Bảng biến thiên:
x

1

y'
y 2


2
Hàm số nghịch biến trên khoảng
;1

và
1;

.Hàm số không có cực
trị.
Cho
0 1
x y
1
0
2
y x
x=2 => y = 5
x=3 => y =
-8 -6 -4 -2 2 4 6 8
-8
-6
-4
-2
2
4
6
8
x
y
I
2đ
0,25
0,25
0,25
0,5
0,25
0,5
2.Tìm m để đường thẳng d:
y x m
cắt (C) tại 2 điểm phân biệt.
Phương trình hoành độ giao điểm:
2 1
1
x
x m
x
(1)
Điều kiện :
1
x
1đ
(1)
2 1 ( )( 1)
x x m x
2
2 1
x x m x mx
2
( 1) 1 0
x m x m
(2)
Đồ thị hàm số (C) và đường thẳng
y x m
cắt nhau tại 2 điểm phân biệt
(1) có 2 nghiệm phân biệt
(2) có 2 nghiệm phân biệt khác 1
2
2
1 ( 1).1 1 0
1 4.1.( 1) 0
m m
m m
2
3 0
6 3 0
m m
3 2 3
3 2 3
m
m
Vậy
( ;3 2 3) (3 2 3; )
m

là giá trị cần tìm.
0,25
0,25
0,25
0,25
2 1.Tính giá trị biểu thức
1 log 3
53
log . . . 8
a
A a a a a
(
0 1
a
)
1 1 1 13 13
535 15 30 10 10
13
log . . . log . . . log
10
a a a
a a a a a a a a a a
2
1 log 3
8
8
27
A=
431
270
1đ
0.25
0,25
0,25
0,25
2.Tìm GTLN và GTNN của hàm số 2
cos cos 2
y x x
Đặt
cos
t x
với
1;1
t .Hàm số trở thành:
2
( ) 2
g t t t
Ta có:
'
2 1
g t t
'
1
0 2 1 0 t =
g t t
Do 1 7
( 1) 4; g ; g(1) 2
2 4
g
nên ta suy ra được:
1;1
1;1
7
max max 4 ; min min
4
t
t
R R
y g t y y
1đ
0,25
0,25
0,25
0,25
3 1đ
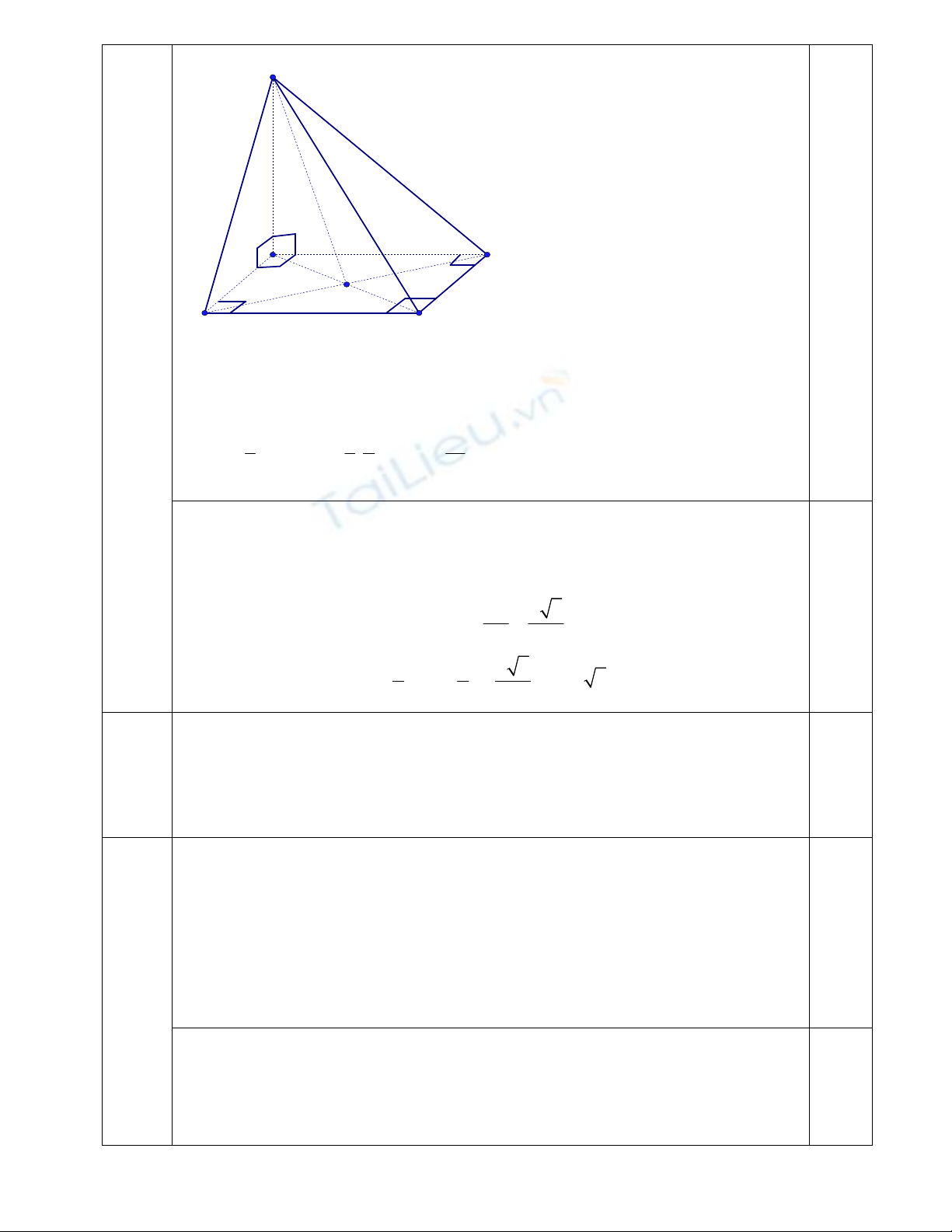
a
a
a
a
2a
O
C
A
D
B
S
1.Tính thể tích khối chóp S.BCD theo a.
Do
( ) ( )
SA ABCD SA BCD
Suy ra SA là đường cao của hình chóp .
S BCD
3
.
1 1 1
. . . . . .2 ( )
3 3 2 3
S BCD BCD
a
V S SA a a a dvtt
0,25
0,25
0,5
2.
Gọi I là trung điểm SC .Do các tam giác SAC , SCD , SBC là các tam giác
vuông có chung cạnh huyền SC
nên ta có IA=IB=IC=ID=IS.
Suy ra I là tâm mc , bán kính mc
6
2 2
SC a
R
Vậy thể tích khối cầu
3
3 3
4 4 6
6
3 3 2
a
V R a
1đ
0,25
0,25
0,25
0,25
4a Viết pttt của đths(C) tại điểm có hoành độ bằng -2
Ta có x =2 => y = 5 => M(2;5)
Hệ số góc của tiếp tuyến
'
2 3
k f
Pttt của đths tại M là y = k(x-x0) +y0 <=> y = -3(x-2)+5 y = -3x + 11
1đ
0,25
0.25
0.5
5a
1.Giải phương trình :
49 10.7 21 0
x x
Đặt t = 7x , t > 0
Pt t2 -10t +21 = 0
7
3
t
t
Với t = 7 7x = 7 7
log 7 1
x x
Với t = 3 7
7 3 log 3
xx
Vậy phương trình có 2 nghiệm x =1 ,
7
log 3
x
1đ
0,25
0,25
0,25
0,25
2.
Điều kiện : 0
0
0
xx
x
Bất pt 2 2
2 2 2 2
log 5 3.2log log 6log 5 0
x x x x
1đ
0,25
0,25
Đặt t = log2
x
Bất pt
22
6 5 0 1;5 1 5 1 log 5 2 32
t t t t x x
So với điều kiện ta được tập nghiệm T=[2;32]
0,5
4b Gọi điểm M(x ; y) là tiếp điểm
Hệ số góc của tiếp tuyến :
' 2 2
0 1
4 3 3 4 0
7
4
3
x y
f x k x x x x x y
=>M( 0 ; 1 ) ,
7
4;
3
N
Phương trình tiếp tuyến tại M : y = 3x + 1
Phương trình tiếp tuyến tại N : y = 3x -
29
3
1đ
0,5
0,25
0,25
5b 1.Cho hàm số
.sin
x
y e x
.Tính
2
2 ''
1
4
y y
theo x
'
''
sin cos .
sin cos . sin . cos . 2cos .
x x
x x x x x
y e x x e
y e x x e x e x e x e
2 2 2
2 ''
2 2 2 2 2
1 1
sin 2 cos
4 4
sin cos
x x
x x x
y y e x e x
e x e x e
1đ
0,25
0,25
0,25
0,25
Gọi 0 0
( ; ) ( )
M x y C
là điểm cần tìm.
M cách đều trục tọa độ
0 0
x y
0 0
0 0
(1)
(2)
y x
y x
2
0 0 0 0
0
2
0 0 0 0
0
0 0
3
(1) ( 1)
1
3 ( 1)
4 0
0 0
x x x x
x
x x x x
x
x y
Vì
M O
nên loại trường hợp này.
2
0 0 0 0
0
2
0 0 0 0
2
0 0
0 0
0 0
0 0
3
(2) ( 1)
1
3 ( 1)
2 2 0
2 ( 1) 0
0 0 (loai)
1 1
x x x x
x
x x x x
x x
x x
x y
x y
Vậy
(1; 1)
M
là điểm cần tìm.
1đ
0,5
0,25
0,25