SỞ GD – ĐT ĐĂK LĂK
TRƯỜNG THPT PHAN CHU TRINH
ĐỀ KIỂM TRA HỌC KỲ II – NĂM HỌC 2012 - 2013
Môn: Toán – Lớp 11 (Ban cơ bản)
Thời gian: 90 phút (không kể thời gian phát đề)
Câu 1: (2,0 điểm) Tính các giới hạn sau:
a)
2
2
3 7 1
lim
4
n n
n n
+ +
+ +
b)
0
9 3
lim
x
x
x
→
+ −
Câu 2: (1,0 điểm) Cho hàm số:
2 3
2
khi 2
( ) 2
2 khi 2
x x x
f x x
mx x
+
≠ −
=+
+ = −
(m là tham số)
Tìm m để hàm số trên liên tục tại điểm x = −2.
Câu 3: (1,5 điểm) Tính đạo hàm của các hàm số sau:
a)
(
)
3 sin
y x x
= +
b)
2
3
1
x x
y
x
− +
=+
Câu 4: (2,5 điểm) Cho hàm số:
3
( ) 3 1
f x x x
= − −
có đồ thị (C).
a) Viết phương trình tiếp tuyến của đồ thị (C):
1) tại điểm
(
)
3;17
A
.
2) biết tiếp tuyến của đồ thị (C) song song với đường thẳng
: 9 1 0
d x y
− + =
.
b) Không dùng máy tính bỏ túi, chứng tỏ phương trình
( ) 0
f x
=
có 3 nghiệm phân biệt
và tìm ba nghiệm đó.
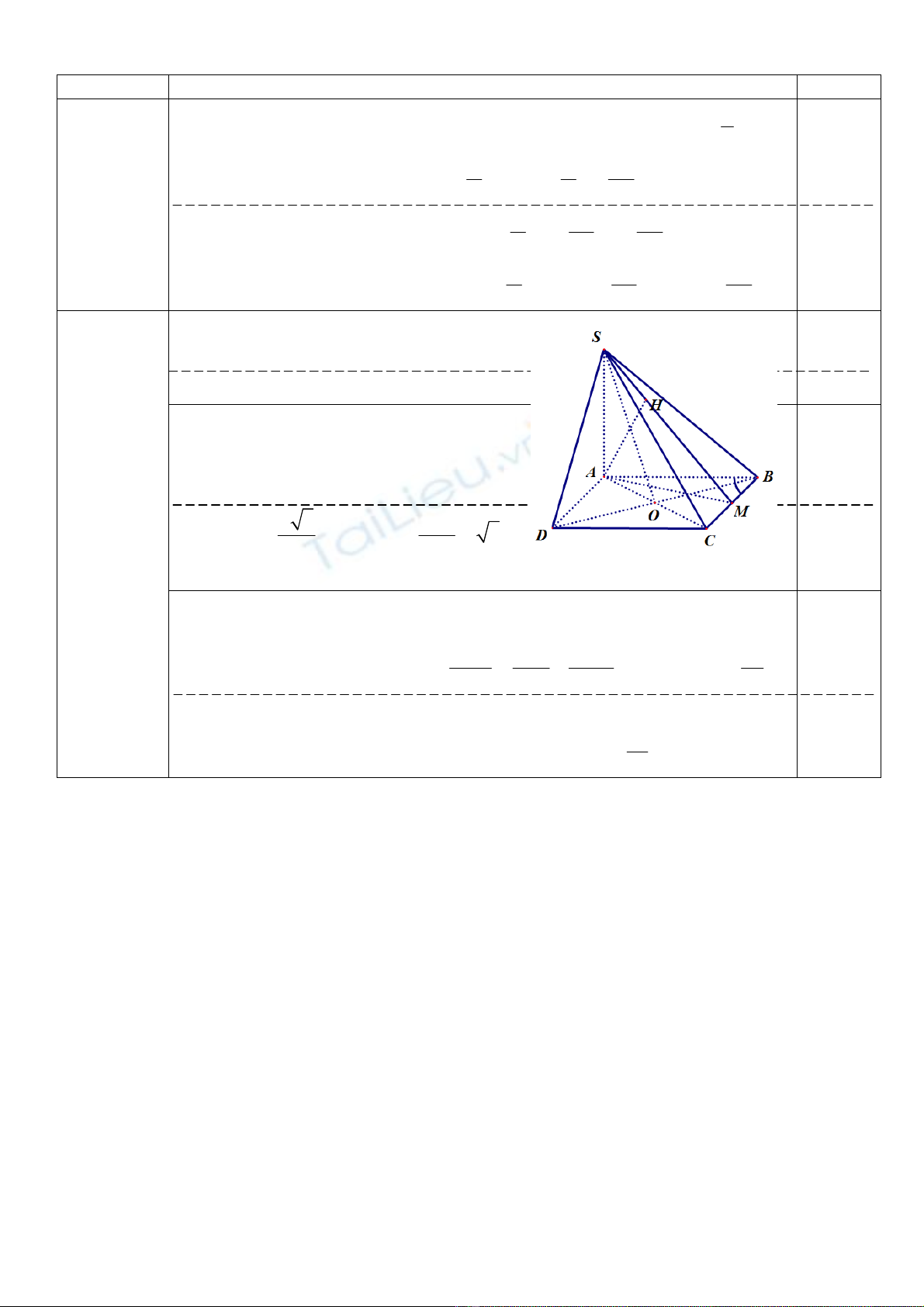
Câu 5: (3,0 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh a và
0
60
ABC
=
. Cạnh bên SA vuông góc với mp(ABCD) và
3
2
SA
=
a
.
a) Chứng minh: (SAC) ⊥ (SBD).
b) Tính góc tạo bởi hai mặt phẳng (ABCD) và (SBC).
c) Tính khoảng cách giữa hai đường thẳng AD và SB.
Sở GD – ĐT ĐăkLăk
Trường THPT Phan Chu Trinh
Năm học: 2012 - 2013
ĐÁP ÁN ĐỀ KIỂM TRA HỌC KỲ II – MÔN TOÁN
LỚP 11 ; NĂM HỌC 2012 – 2013
(Đáp án – Thang điểm này gồm 2 trang)
................
...............
Câu Đáp án Điểm
Câu 1:
( 2,0 điểm)
22
2
2
7 1
3
3 7 1
lim lim 3
1 4
41
n n n n
n n
n n
+ +
+ +
= =
+ + + +
( )
0 0
9 3 1 1
lim lim
2 12
2 9 3
x x
x
xx
→ →
+ −
= =
+ +
1,0
1,0
Câu 2:
( 1,0 điểm)
Tập xác định:
D R
=
( 2) 2 2
f m
− = −
2 3
2 2
2
lim ( ) lim 4
x x
x x
f x
x
→− →−
+
= =
+
Hàm số
( )
f x
liên tục tại x = −2 khi và chỉ khi:
2
lim ( ) ( 2)
x
f x f
→−
= −
⇔
1
= −
0,25
0,5
0,25
Câu 3:
( 1,5 điểm)
(
)
(
)
(
)
' 3 '.sin 3 sin '
y x x x x
= + + +
(
)
sin 3 cos
x x x
= + +
0,75
(
)
(
)
(
)
(
)
( ) ( )
2 2 2
2 2
3 '. 1 1 '. 3
2 4
'1 1
x x x x x x x x
yx x
− + + − + − +
+ −
= =
+ +
0,75
Câu 4:
( 2,5 điểm)
Ta có:
2
'( ) 3 3
f x x
= −
Ph
ươ
ng trình ti
ế
p tuy
ế
n c
ủ
a
đồ
th
ị
(C) t
ạ
i
đ
i
ể
m
(
)
3;17
A.
(
)
17 '(3) 3
y f x
− = −
⇔
24 55
y x
= −
Ta có:
:9 1 0
d x y
− + =
⇔
9 1
y x
= +
có h
ệ
s
ố
góc
9
=
Vì ti
ế
p tuy
ế
n c
ủ
a
đồ
th
ị
(C) song song v
ớ
i
đườ
ng th
ẳ
ng d nên
'( ) 9
f x
=
⇔
2
3 3 9
x
− =
⇔
2
x
= ±
2 3
x y
= − ⇒= −
, pttt:
9 15
y x
= +
2 1
x y
=⇒=
, pttt:
9 17
y x
= −
0,25
0,5
0,25
0,25
0,25
Xét hàm số
3
( ) 3 1
f x x x
= − −
xác định và liên tục trên R
( 2) 3
f
− = −
;
( 1) 1
f
− =
;
(0) 1
f
= −
;
(2) 1
f
=
Vì
( 2). ( 1) 3 0
f f
− − = − <
nên phương trình
( ) 0
f x
=
có ít nhất một nghiệm
thuộc khoảng
(
)
2; 1
− −
Vì
( 1). (0) 1 0
f f
− = − <
nên phương trình
( ) 0
f x
=
có ít nhất một nghiệm
thuộc khoảng
(
)
1;0
Vì
(0). (2) 1 0
f f
= − <
nên phương trình
( ) 0
f x
=
có ít nhất một nghiệm
thuộc khoảng
(
)
0;2
Mặt khác
( ) 0
f x
=
là phương trình bậc 3 nên có nhiều nhất 3 nghiệm. Vậy
pt
( ) 0
f x
=
có 3 nghiệm phân biệt
Theo chứng minh trên 3 nghiệm phân biệt thuộc khoảng
(
)
2;2
nên ta chỉ
cần tìm 3 nghiệm trong khoảng này. Đặt
2cos
x t
vớ
i
(
)
0;
t
π
0,25
0,25
Câu Đáp án Điểm
Ph
ươ
ng trình tr
ở
thành:
3
8cos 6cos 1 0
t t
− − =
⇔3
1
4cos 3cos
2
t t
− =
⇔
cos3 cos
3
t
π
=
⇔
2
9 3
t k
π π
= ± +
V
ớ
i
(
)
0;
t
π
, ta ch
ỉ
có các nghi
ệ
m:
9
t
π
=
;
5
9
t
π
=
;
7
9
t
π
=
V
ậ
y pt
( ) 0
f x
=
có 3 nghi
ệ
m:
2cos
9
x
π
=
;
5
2cos
9
x
π
=
;
7
2cos
9
x
π
=
0,25
0,25
Câu 5:
( 3,0 điểm)
(SAC)
BD AC BD
BD SA
⊥⇒⊥
⊥
Mà
( )
BD SBD
nên (SAC)
⊥
(SBD)
0,5
0,25
G
ọ
i M là trung
đ
i
ể
m BC,
∆
ABC
đề
u nên BC
⊥
AM, BC
⊥
SA (gt)
Do
đ
ó góc gi
ữ
a hai m
ặ
t ph
ẳ
ng
(ABCD) và (SBC) là góc
SMA
Tính
3
2
a
AM =
,
tan 3
SA
SMA
AM
= =
⇒
0
60
SMA
=
0,25
0,25
0,25
Ch
ứ
ng minh (SAM)
⊥
(SBC), trong tam giác SAM t
ừ
A k
ẻ
AH
⊥
SM t
ạ
i H
thì AH
⊥
(SBC)
Tam giác SAM vuông t
ạ
i A nên:
2 2 2
1 1 1
AH AS AM
= +
, suy ra:
3
4
a
AH =
Vì AD // (SBC) nên
(
)
(
)
, ,( )
d AD SB d AD SBC
( )
3
,( )
4
d A SBC AH
a
= = =
0,5
0,5
Chú ý: Hướng dẫn chấm này chỉ trình bày sơ lược một cách giải , trong bài làm học sinh phải
trình bày chặt chẽ mới đạt điểm tối đa .Nếu học sinh có cách giải khác với đáp án mà đúng vẫn
đạt được điểm tối đa. Điểm toàn bài phải làm tròn đến 0,5.
Hình vẽ đúng 0,5