0
TRUNG TÂM GDTX ANH SƠN ĐỀ KIỂM TRA HỌC KỲ II LỚP 11
====== ==== Khóa ngày 14 tháng 05 năm 2010
MÔN TOÁN
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
Câu 1 (2,0 điểm) Tính các giới hạn sau:
1) 2
2
6 8
lim
2
x
x x
x
3) 1
5 1 2
lim
1
x
x
x
2)
2
lim 3 1
n x n
4) 5
2 7
lim
5
x
x
x
Câu 2 (1,5 điểm) Cho hàm số
22
-1
( ) 1
3 5 -1
x x khi x
y f x x
m khi x
.
Xác định m để hàm số liên tục tại
1
x
.
Câu 3 (3,5 điểm)
1. Tính đạo hàm của các hàm số sau:
a) 2
2 6 5
2 4
x x
y
x
b) 2
1.sin 2
y x x
2. Cho hàm số 3 2
5
y x x x
(C). Viết phương trình tiếp tuyến với (C)
a) Tại điểm
( 1; 6)
A
b) Biết tiếp tuyến song song với đường thẳng
( ) : 6 2010
d y x
c) Tại giao điểm của (C) với đường thẳng
5
y
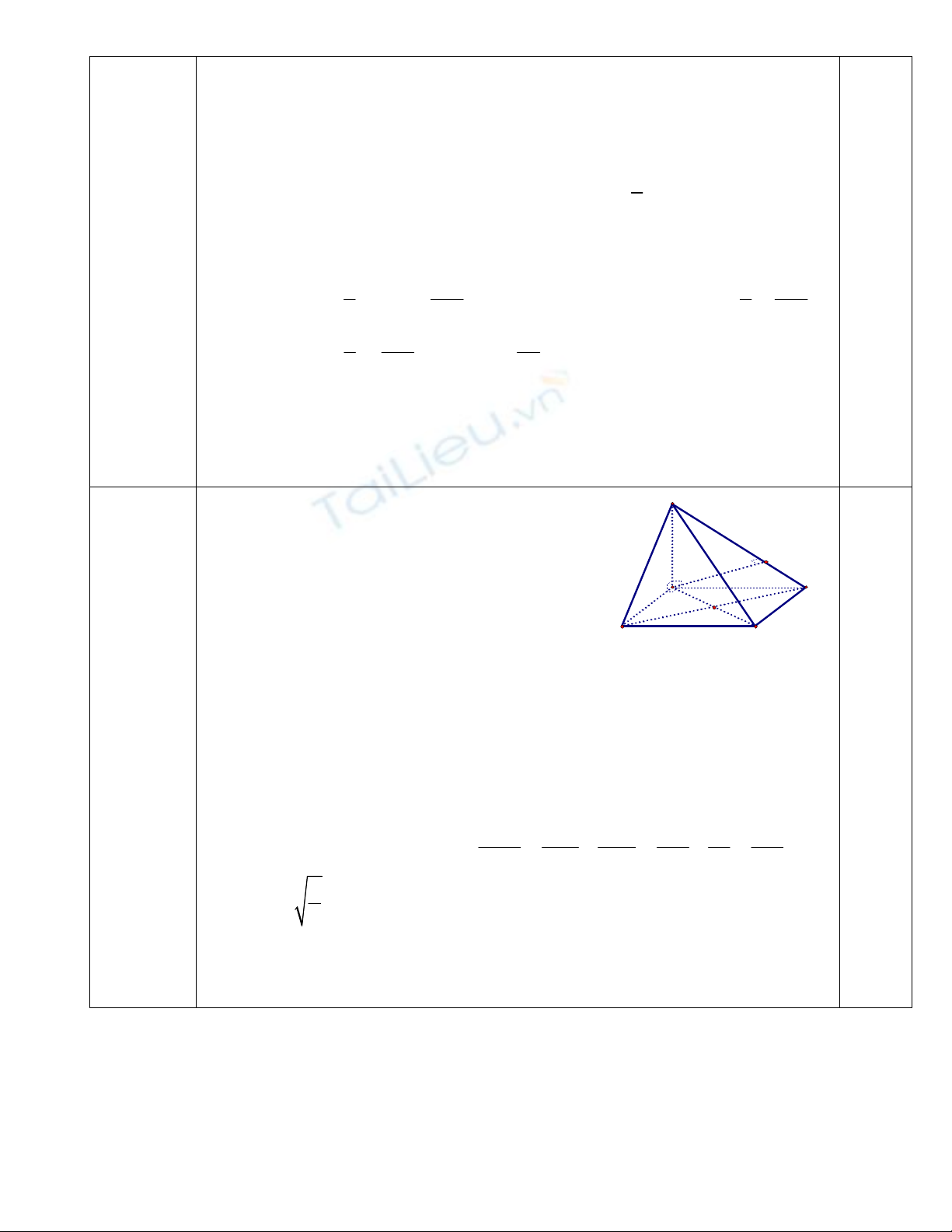
Câu 4 (3,0 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc
với đáy.
2
SA a
.
1) Chứng minh rằng các mặt bên của hình chóp là những tam giác vuông.
2) Tính khoảng cách từ điểm A đến mặt phẳng (SBC)
3) Xác định đường vuông góc chung của BD và SC.
-------------------------------HẾT-----------------------------
Thí sinh không được sử dụng tài liệu. Giám thị coi thi không giải thích gì thêm.
ĐỀ CHÍNH THỨC
1
ĐÁP ÁN – THANG ĐIỂM
CÂU ĐÁP ÁN ĐIỂM
Câu 1
( 2,0
điểm)
1) 2
2
6 8
lim
2
x
x x
x
= 2
( 2)( 4)
lim
2
x
x x
x
= 2
lim( 4)
xx
=
2 4 2
2)
2
lim 3 1
n x n
=
2
3 1
lim 3 1
n
n n n
=
2
1
3
lim 3 1
1 1
n
n n
=
3 0 3
2
1 0 0 1
3) 1
5 1 2
lim
1
x
x
x
=1
5 5
lim
( 1)( 5 1 2)
x
x
x x
=1
5
lim
5 1 2
xx
=
5 5
4
5.1 1 2
4) Vì 5
lim(2 7) 2.5 7 3 0
xx
5
lim(5 ) 0
xx
và
5 0 , 5
x x
Vậy 5
2 7
lim
5
x
x
x

0,25 đ
0,25 đ
0,25 đ
0,25 đ
0,25 đ
0,25 đ
0,25 đ
0,25 đ
Câu 2
(1,5 điểm)
Ta có
( 1) 3 5
f m
.
2
1
2
lim
1
x
x x
x

=1
( 1)( 2)
lim
1
x
x x
x

=1
lim( 2) 3
xx

Vậy hàm số liên tục tại
1
x
khi và chỉ khi
3 5 3
m
hay
8
3
m
0,25 đ
0,5 đ
0,5 đ
0,25 đ
Câu 3
(3,5 điểm)
1. a)
Ta có 2 2
2
(2 6 5)'(2 4) (2 6 5)(2 4)'
'(2 4)
x x x x x x
yx
2
2
(4 6)(2 4) 2(2 6 5)
(2 4)
x x x x
x
2
2
4 16 34
(2 4)
x x
x
b) Ta có 2 2
' ( )' 1 ( 1)'
y x x x x
=2
2
1
1
x
xx
= 2
2
2 1
1
x
x
2. Ta có 2
' 3 2 1
y x x
a) 2
'( 1) 3( 1) 2( 1) 1 2
y
0,25 đ
0,25 đ
0,25 đ
0,25 đ
0,25 đ
0,25 đ
2
Phương trình tiếp tuyến tại
( 1; 6)
A
là
2( 1) 6
y x
hay
2 4
y x
b) Do tiếp tuyến song song với
( ) : 6 2010
d y x
nên tiếp tuyến có hệ
số góc
6
k
Hay 2
3 2 1 6
x x
2
3 2 5 0
x x
1
5
3
x
x
Với
1
x
2
y
. Phương trình tiếp tuyến tại điểm
(1; 2)
M
là
6( 1) 2
y x
6 8
y x
Với
5 230
3 27
x y . Phương trình tiếp tuyến tại
5 230
( ; )
3 27
N :
5 230 40
6( ) 6
3 27 27
y x y x
c) Phương trình hoành độ giao điểm của (C) với đường thẳng
5
y
là
3 2
5 5
x x x
3 2 2
0 ( 1) 0 0
x x x x x x x
'(0) 1
y
. Phương trình tiếp tuyến tại điểm
(0; 5)
P
là:
1( 0) 5 5
y x y x
0,5 đ
0,25 đ
0,25 đ
0,25 đ
0,25 đ
0,25 đ
0,25 đ
Câu 4
(3,0 điểm)
1) Ta có ( )
SA AB
SA ABCD
SA AD
suy ra
SAB
và
SAD
vuông tại A
Vì ABCD là hình vuông nên
CB AB
Và
( ( ))
CB SA do SA ABCD
suy
ra ( )
CB SAB CB SB
. Vậy
SBC
vuông tại B.
Chứng minh tương tự ta có
SCD
vuông tại D.
2)
( ) ( ) ( )
CB SAB SBC SAB
( theo câu a). Trong mp(SAB) dựng AH
vuông góc SB, suy ra ( ,( ))
d A SBC AH
.
Xét
SAB
vuông tại A nên ta có
2 2 2 2 2 2
1 1 1 1 1 3
2 2
AH AS AB a a a
2
3
AH a .
3) Gọi O là giao điểm của AC và BD. Trong
SAC
dựng
( )
OI SC I SC
suy ra OI là đường vuông góc chung của BD và SC.
Thật vậy ( )
BD SAC BD OI
.
0,25 đ
0,25 đ
0,25 đ
0,25 đ
0,5 đ
0,5 đ
0,5 đ
0,5 đ
Ngày 05 tháng 05 năm 2010
Giáo viên:
KIỀU ĐÌNH TUẤN
S
H
O
C
A
B
D