ĐỀ SỐ 3
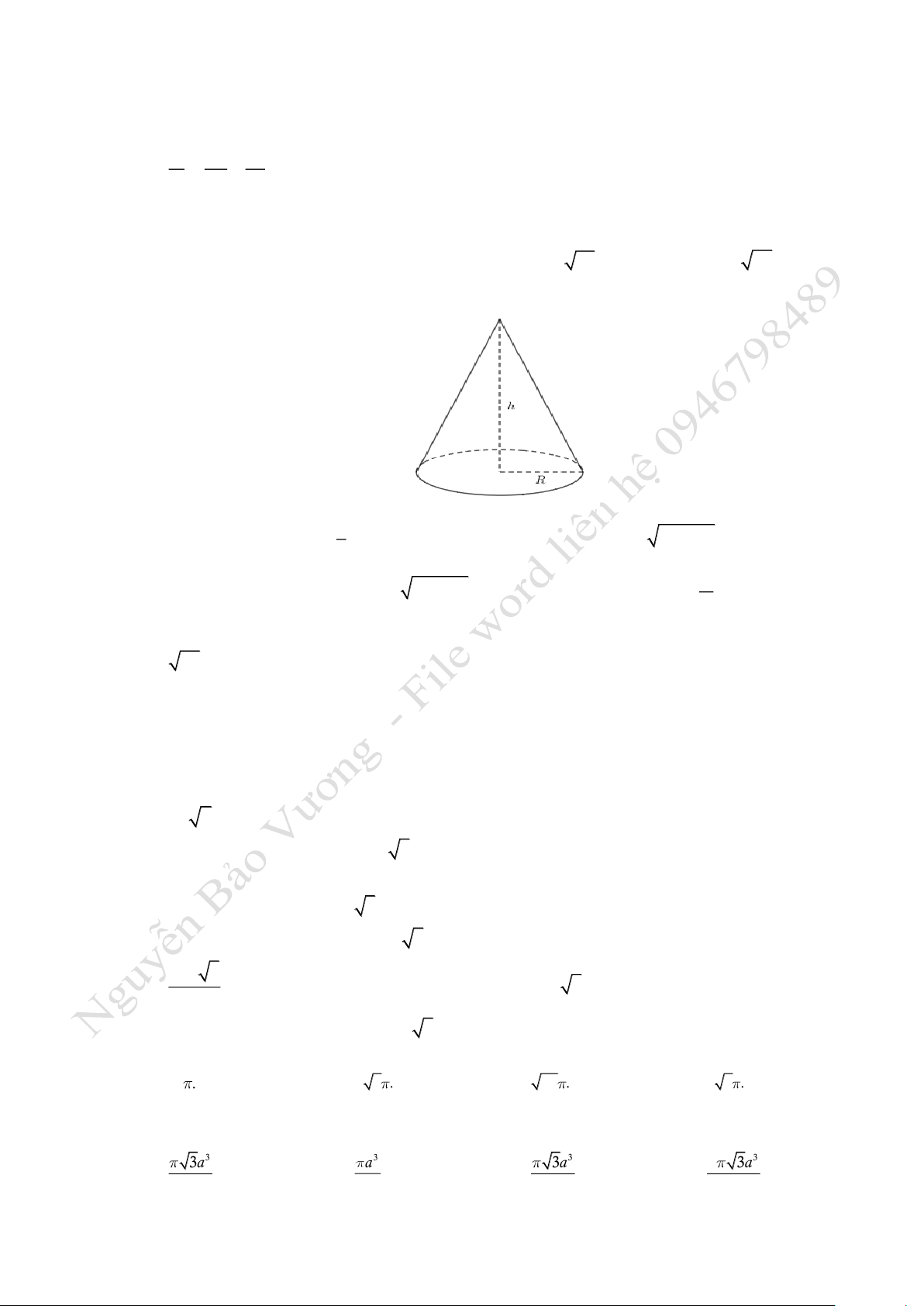
Câu 1. Gọi
, , l h R
lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón. Mệnh đề
nào sau đây đúng?
A.
2 2 2
1 1 1
l R h
=+
. B.
2 2 2
l h R=+
. C.
2 2 2
R h l=+
. D.
2
l hR=
.
Câu 2. Cho hình nón tròn xoay có đường cao
20 cmh=
, bán kính đáy
25 cmr=
. Độ dài đường sinh
của hình nón bằng
A.
26 cml=
. B.
28 cml=
. C.
5 41 cml=
. D.
6 30 cml=
.
Câu 3. Hình nón có đáy là hình tròn bán kính
R
, chiều cao
h
. Mệnh đề nào sau đây sai?
A. Thể tích khối nón
2
1
3
V R h
=
. B. Đường sinh
22
l h R=+
.
C. Diện tích xung quanh
22
xq
S R R h
=+
. D. Góc ở đỉnh
arctan R
h
=
.
Câu 4. Cho khối nón có bán kính đáy
3,r=
độ dài đường sinh
5l=
. Chiều cao
h
của khối nón bằng:
A.
34
. B.
5
. C.
4
. D.
3
.
Câu 5. Một hình nón có bán kính đường tròn đáy bằng 40 cm, độ dài đường sinh bằng 44 cm. Thể tích
V
của khối nón này có giá trị gần đúng với giá trị nào sau đây?
A.
30700
cm3. B.
92090
cm3. C.
30679
cm3. D.
92100
cm3.
Câu 6. Một hình nón có bán kính 5a, độ dài đường sinh bằng 13a. Độ dài đường cao h của hình nón
bằng
A.
76a
. B.
12a
. C.
17a
. D.
8a
.
Câu 7. Một hình nón có chiều cao
3ha=
và bán kính đáy
ra=
. Diện tích xung quanh của hình
nón bằng
A.
2
2a
. B.
2
3a
. C.
2
a
. D.
2
2a
.
Câu 8. Cho khối nón có bán kính đáy
3r=
và chiều cao
4h=
. Thể tích của khối nón bằng
A.
16 3
3
. B.
4
. C.
16 3
. D.
12
.
Câu 9. Cho hình nón có bán kính đáy
3r=
và độ dài đường sinh
4.l=
Diện tích xung quanh của
hình nón là
A.
12 .
B.
4 3 .
C.
39 .
D.
83.
Câu 10. Người ta đặt được một tam giác đều
ABC
cạnh là
2a
vào một hình nón sao cho
A
trùng với
đỉnh của hình nón, còn
BC
đi qua tâm của mặt đáy hình nón. Thể tích
V
của khối nón bằng
A.
3
3.
6
a
B.
3
.
3
a
C.
3
3.
3
a
D.
3
23
.
3
a
Câu 11. Cắt một khối nón bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác đều
cạnh bằng
2
. Diện tích xung quanh của khối nón bằng
A.
3
. B.
4
. C.
2
. D.
.
Câu 12. Cho hình nón đỉnh
S
, đáy là hình tròn tâm
O
, thiết diện qua trục là tam giác đều cạnh
a
. Thể
tích của khối nón bằng
A.
33
24
a
. B.
33
8
a
. C.
33
4
a
. D.
33
2
a
.
Câu 13. Cắt một hình nón bằng một mặt phẳng đi qua trục của nó ta được thiết diện là một tam giác
vuông cân có cạnh huyền bằng
a
. Diện tích xung quanh của hình nón theo
a
.
A.
22
4
a
. B.
22
2
a
. C.
2
a
. D.
22a
.
Câu 14. Cho hình nón có thiết diện qua trục là một tam giác đều và khoảng cách từ tâm của đáy đến
đường sinh bằng
3
2
a
. Tính diện tích toàn phần của hình nón.
A.
2
3
tp
Sa
=
. B.
2
5
tp
Sa
=
. C.
2
2
tp
Sa
=
. D.
2
4
tp
Sa
=
.
Câu 15. Một hình nón đỉnh
S
đáy hình tròn tâm
O
và
SO h=
. Một mặt phẳng
( )
P
qua đỉnh
S
cắt
đường tròn
( )
O
theo dây cung
AB
sao cho góc
90AOB =
, biết khoảng cách từ
O
đến
( )
P
bằng
2
h
. Diện tích xung quanh của hình nón bằng
A.
210
6
h
. B.
210
33
h
. C.
210
3
h
. D.
2
2 10
3
h
.
Câu 16. Trong không gian, cho tam giác
ABC
vuông tại
,A AB a=
và
3AC a=
. Độ dài đường sinh
l
của hình nón nhận được khi quay tam giác
ABC
xung quanh trục
AB
.
A.
a
. B.
2a
. C.
3a
. D.
2a
.
Câu 17. Trong không gian, cho tam giác
ABC
vuông tại
,2A AC a=
,
30o
ABC =
. Tính độ dài đường
sinh
l
của hình nón nhận được khi quay tam giác
ABC
quanh trục
AB
.
A.
4a
. B.
3a
. C.
3
2
a
. D.
2a
.
Câu 18. Trong không gian cho tam giác
ABC
vuông tại
,A AB a=
và
30o
ACB =
. Tính thể tích
V
của
khối nón nhận được khi quay tam giác
ABC
quanh cạnh
AC
.
A.
33
3
a
. B.
33
9
a
. C.
33a
. D.
3
a
.
Câu 19. Cho tam giác
ABC
vuông tại
,A
,AB a
3.AC a
Quay tam giác đó quanh đường thẳng
BC
ta được khối tròn xoay. Tính thể tích
V
của khối tròn xoay này.
A.
3
2
a
. B.
3
23a
. C.
3
4
a
. D.
3
3
a
.
Câu 20. Cho tam giác
ABC
có
3,AB
5,BC
7.CA
Tính thể tích
V
của khối tròn xoay sinh ra do
hình tam giác
ABC
quay quanh đường thẳng
.AB
A.
50
. B.
75
4
. C.
275
8
. D.
125
8
.
Câu 21. Cho tam giác
ABC
vuông tại
A
có
0
30ABC =
và cạnh góc vuông
2AC a=
quay quanh cạnh
AC
tạo thành hình nón tròn xoay. Diện tích xung quanh của hình nón bằng:
A.
2
16 3a
. B.
2
83a
. C.
2
2a
D.
2
43
3a
.
Câu 22. Cho tam giác
ABC
có
3AB =
,
4AC =
,
5BC =
. Thể tích
V
của vật thể tròn xoay khi quay
ABC
quanh cạnh
AC
là
A.
12
. B.
11
. C.
10
. D.
13
.
Câu 23. Cho tam giác
ABC
vuông tại
A
có
3AB a=
,
4AC a=
. Khi tam giác
ABC
quay quanh đường
thẳng
BC
ta được một khối tròn xoay. Tính thể tích
V
của khối tròn xoay đó.
A.
3.a
B.
3
96 .
5a
C.
3
3.a
D.
3
48 .
5a
Câu 24. Cho tam giác
ABC
vuông tại
A
có
6AB =
,
8AC =
. Tính diện tích xung quanh
xq
S
của hình
nón tròn xoay khi quay tam giác
ABC
quanh cạnh
AC
.
A.
160 .
B.
80 .
C.
120 .
D.
60 .
Câu 25. Cho tam giác
OAB
vuông tại
O
có
3, 4OA OB==
. Tính diện tích toàn phần của hình nón tạo
thành khi quay tam giác
OAB
quanh
OA
.
A.
36
. B.
20
. C.
26
. D.
52
.
Câu 26. Tam giác
ABC
vuông tại
B
có
3,AB a BC a==
. Khi quay hình tam giác đó quanh đường
thẳng
AB
một góc
0
360
ta được một khối tròn xoay. Tính thể tích
V
của khối tròn xoayđó.
A.
3.Va=
B.
3
2
a
V=
. C.
3
3
a
V=
. D.
3
3Va=
.
Câu 27. Mặt cầu
()S
ngoại tiếp hình chóp tứ giác đều có cạnh bên và cạnh đáy bằng
a
. Hỏi đường kính
mặt cầu
()S
A.
a
. B.
2a
. C.
2a
. D.
2
2
a
.
Câu 28. Cho hình chóp
.S ABC
có đáy là tam giác
ABC
vuông cân tại
B
,
AB a=
, biết
2SA a=
và
()SA ABC⊥
, Gọi
H
và
K
lần lượt là hình chiếu của
A
trên các cạnh
SB
và
SC
. Xác định
tâm
I
và tính bán kính
R
của mặt cầu qua các điểm
, , , ,A B C H K
A.
I
là trung điểm
,2AC R a=
. B.
I
là trung điểm
2
,2
a
AC R =
.
C.
I
là trung điểm
,AB R a=
. D.
I
là trung điểm
,2
a
AB R =
.
Câu 29. Các bán kính đáy của khối nón cụt lần lượt là
x
và
3x
, đường sinh là
2,9x
. Tính thể tích khối
nón cụt đó theo
x
.
A.
3
77
10x
V
=
. B.
3
3
x
V
=
. C.
32
93
x
V
=
. D.
3
91
10x
V
=
.
Câu 30. Một đống cát hình nón cụt có chiều cao
60h cm=
, bán kính đáy lớn
11Rm=
, bán kính đáy nhỏ
250R cm=
. Tính thể tích V của đống cát (lấy xấp xỉ).
A.
3
0,11m
. B.
3
0,1m
. C.
3
1,1m
. D.
3
11m
.
Câu 31. Tính thể tích
V
của khối nón tròn xoay thu được khi quay hình thang
ABCD
quanh trục
'OO
như hình vẽ. Biết
' 200OO =
,
' 20OD=
,
' 10OC=
,
10OA =
và
5OB =
.
A.
75000V
=
. B.
40000V
=
. C.
35000V
=
. D.
37500V
=
.
Câu 32. Từ cùng một tấm kim loại dẻo hình quạt (như hình vẽ) có bán kính
5R=
và chu vi của hình
quạt là
4 10P
=+
, người ta gò tấm phim loại đó thành những chiếc phễu hình nón theo hai
cách
Cách 1: Gò tấm kim loại ban đầu thành mặt xung quanh của cái phễu.
Cách 2: Chia đôi tấm kim loại thành hai phần bằng nhau rồi gò thành mặt xung quanh của hai
cái phễu.
Gọi
1
V
là thể tích của cái phễu ở cách 1 và
2
V
là tổng thể tích của hai cái phễu ở cách 2. Tính tỉ
số
1
2
V
V
.
A.
0,373
. B.
0,412
. C.
1,871
. D.
1,780
.
Câu 33. Một tứ diện đều cạnh a có một đỉnh trùng với đỉnh của một hình nón, ba đỉnh còn lại nằm trên
đường tròn đáy của hình nón đó. Tính diện tích xung quanh của hình nón.
A.
2
3
3
xq a
S
=
. B.
2
2
3
xq a
S
=
. C.
2
2
xq
Sa
=
. D.
2
3
2
xq a
S
=
Câu 34. Bên trong hình vuông cạnh
a
, dựng hình sao 4 cánh đều như hình vẽ bên ( các kích thước cần
thiết cho như ở trong hình vẽ bên).
Tính thể tích
V
của khối tròn xoay sinh ra khi quay hình bên quanh trục
xy
.
A.
3
548
a
V
=
. B.
3
516
a
V
=
. C.
3
6
a
V
=
. D.
3
8
a
V
=
.
Câu 35. Cho tứ diện đều
ABCD
có cạnh bằng
3a
. Hình nón
( )
N
đỉnh
A
và đường tròn đáy là đường
tròn ngoại tiếp tam giác
BCD
. Tính diện tích xung quanh
xq
S
của
( )
N
.
A.
2
6.
xq
Sa
=
B.
2
3 3 .
xq
Sa
=
C.
2
12 .
xq
Sa
=
D.
2
6 3 .
xq
Sa
=
Câu 36. Tính diện tích xung quanh
xq
S
của hình nón tròn xoay nội tiếp trong tứ diện đều có cạnh bằng
a
.
A.
2.
4
xq a
S
=
B.
22.
6
xq a
S
=
C.
2.
2
xq a
S
=
D.
23.
6
xq a
S
=
Câu 37. Cho hình chóp tứ giác đều
.S ABCD
có các cạnh đều bằng
2a
. Tính thể tích
V
của khối nón
có đỉnh
S
và đường tròn đáy là đường tròn nội tiếp tứ giác
ABCD
.
A.
3
2
=a
V
. B.
3
26
=a
V
. C.
3
6
=a
V
. D.
3
22
=a
V
.
Câu 38. Cho hình nón
( )
N
có đỉnh là
S
, đường tròn đáy là
( )
O
có bán kính
R
, góc ở đỉnh của hình
nón là
120
=
. Tính thể tích
V
của hình chóp đều
.S ABCD
có các đỉnh
, , ,A B C D
thuộc
đường tròn
( )
O
.
A.
3
23
3R
. B.
3
23
9R
. C.
3
3
3
R
. D.
3
29
R
.
Câu 39. Cho hình chóp đều
.S ABC
có cạnh đáy bằng
a
, góc giữa mặt bên và đáy bằng
0
60
. Tính diện
tích xung quanh
xq
S
của hình nón đỉnh
S
, đáy là đường tròn ngoại tiếp tam giác
ABC
.
A.
2
3
3
xq a
S
=
. B.
2
10
8
xq a
S
=
. C.
2
7
4
xq a
S
=
. D.
2
7
6
xq a
S
=
.
Câu 40. Một hình chóp tam giác đều có đỉnh trùng với đỉnh của hình nón và các đỉnh còn lại nằm trên
đường tròn đáy của hình nón. Gọi
1
V
là thể tích khối chóp tam giác đều và
2
V
là thể tích của
khối nón. Hãy xác định tỉ số
1
2
k
V
V
.
A.
33k
. B.
33
2
k
. C.
33
4
k
. D.
3
2
k
.