ĐỀ SỐ 4
Câu 1. Thể tích
V
của khối nón tròn xoay có bán kính đáy
r
và chiều cao
h
được cho bởi công thức
nào dưới đây?
A.
2
1
3
V r h
=
. B.
2
4
3
V r h
=
. C.
2
V r h
=
. D.
22
V r h
=
.
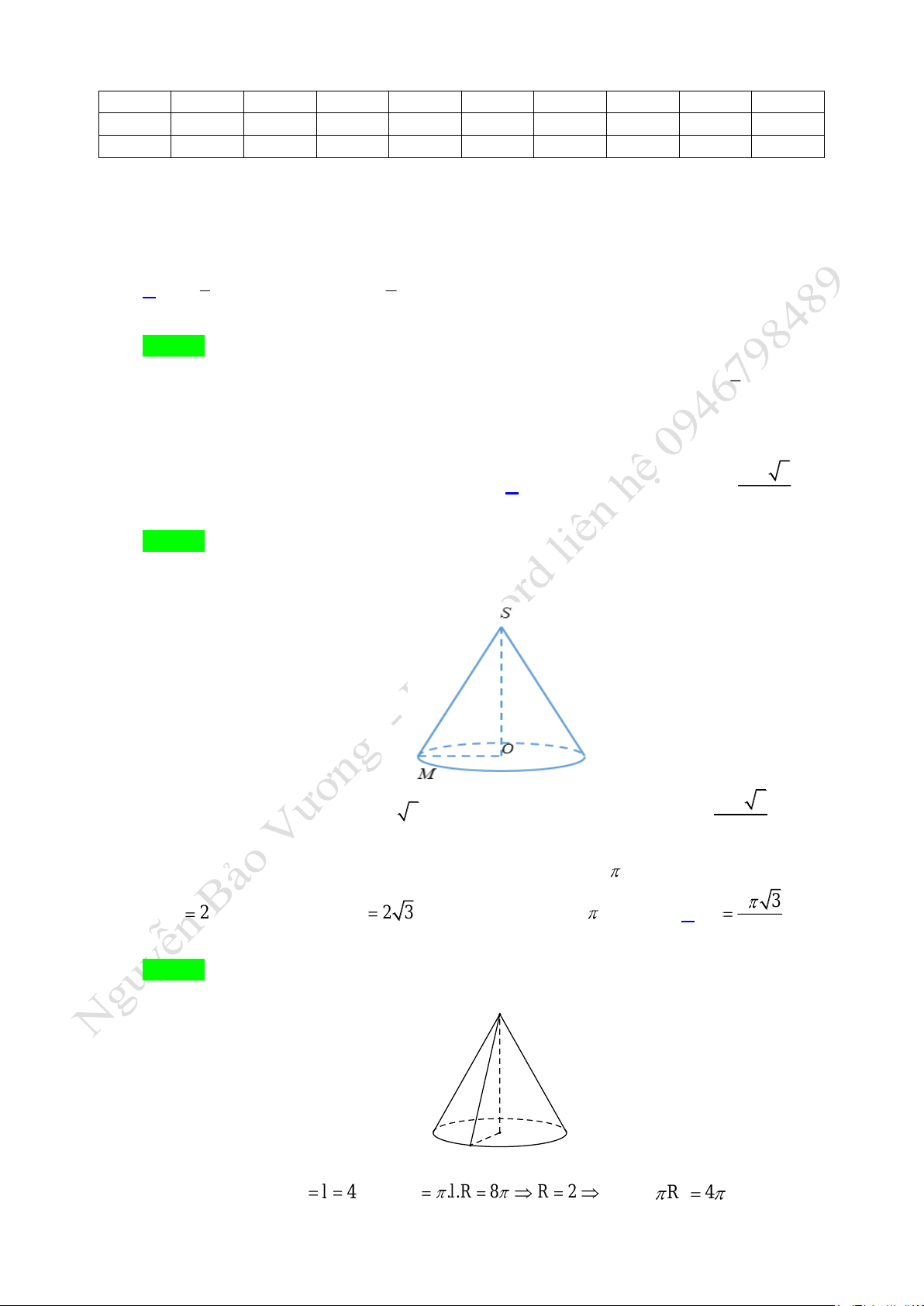
Câu 2. Cho hình nón có đỉnh
S
, tâm đáy là
O
, bán kính đáy là
a
, góc tạo bởi một đường sinh
SM
và
đáy là
60o
. Tìm kết luận sai?
A.
2la=
. B.
2
2
xq
Sa
=
. C.
2
4
tp
Sa
=
. D.
33
3
a
V
=
.
Câu 3. Cho hình nón đỉnh O, tâm đáy là I, đường sinh OA = 4, Sxq =
8
. Tìm kết luận sai:
A.
2R
. B.
23h
. C. Sđáy =
4
. D.
43
3
V
.
Câu 4. Thiết diện qua trục của một hình nón là một tam giác vuông cân, cạnh góc vuông là a. Tìm kết
luận đúng?
A.
32
9
a
V
. B.
32
3
a
V
. C.
32
12
a
V
. D.
32
6
a
V
.
Câu 5. Một hình nón có đường cao
20
h cm
=
, bán kính đáy
25
r cm
=
. Diện tích xung quanh của hình
nón đó bằng
A.
5 41
. B.
25 41
. C.
75 41
. D.
125 41
.
Câu 6. Cho hình nón có bán kính đáy là
4
a
, đường sinh là
5
a
. Thể tích của khối nón là
A.
3
48
a
. B.
3
40
a
. C.
3
24
a
. D.
3
16
a
.
Câu 7. Cho hình nón có bán kính đáy là
3a
, chiều cao là
4a
. Thể tích của khối nón là:
A.
3
15 a
. B.
3
36 a
. C.
3
12 a
. D.
3
18 a
.
Câu 8. Cho tam giác đều
ABC
cạnh
a
quay xung quanh đường cao
AH
tạo nên một hình nón. Diện
tích xung quanh của hình nón đó là:
A.
2
a
. B.
2
2a
. C.
2
1
2a
. D.
2
3
4a
.
Câu 9. Cho hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh huyền
2a
. Thể tích của
khối nón bằng:
A.
3
3
a
. B.
3
23a
. C.
3
2
a
. D.
3
6
a
.
Câu 10. Cho hình nón có thiết diện qua trục của nó là một tam giác vuông cân có cạnh huyền
2a
.
Diện tích xung quanh của hình nón là
A.
23
3
a
. B.
22
3
a
. C.
22
6
a
. D.
22
2
a
.
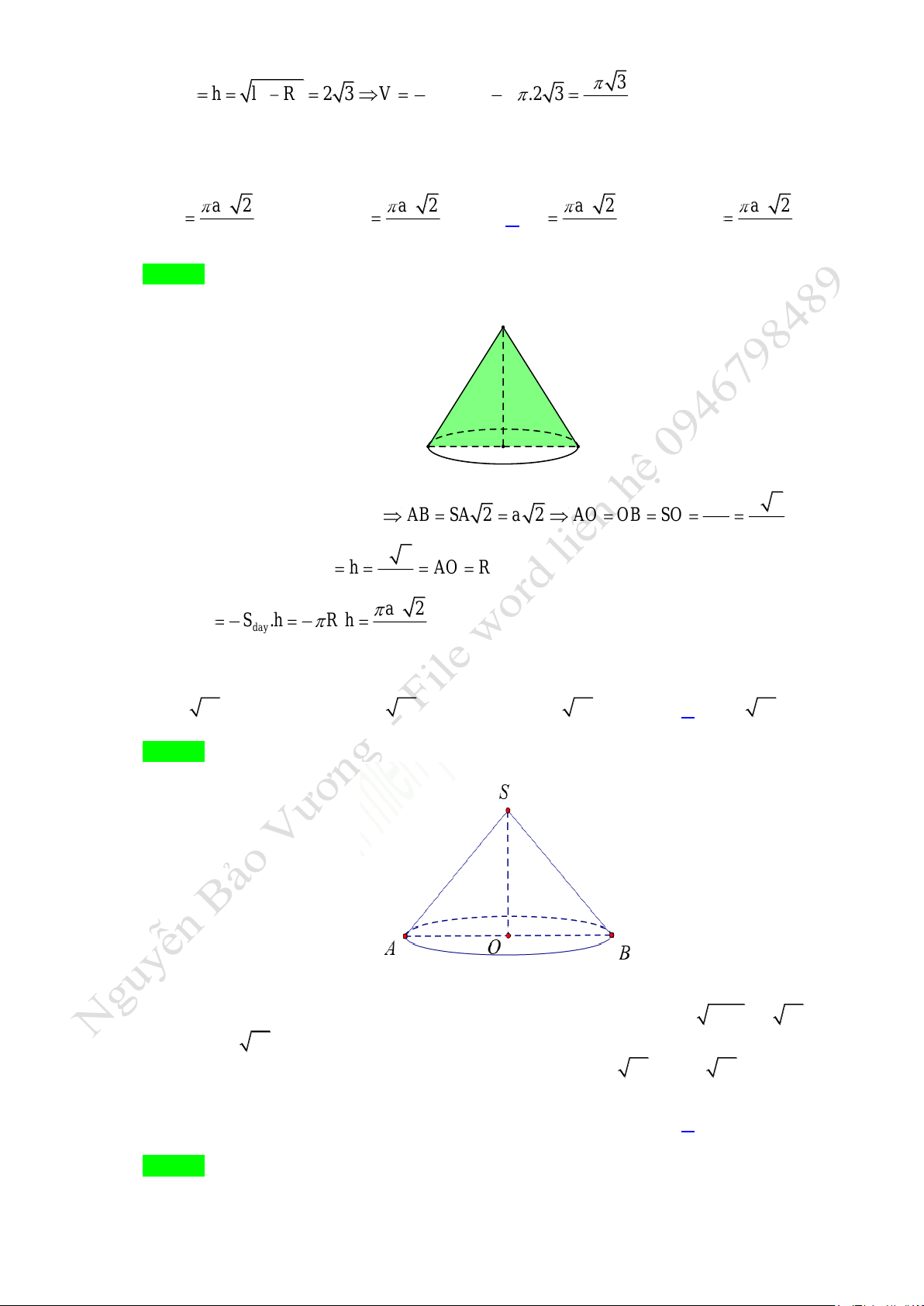
Câu 11. Cho hình nón đỉnh S, tâm đáy là O, hai đường sinh SA, SB bằng 4 và tạo với nhau một góc
60
và
ABO
vuông tại O. Tìm kết luận đúng
A.
2R=
. B.
22R=
. C.
4R=
. D.
43R=
.
Câu 12. Thiết diện qua trục của một hình nón là tam giác đều cạnh
6cm
. Thiết diện qua 2 đường sinh
tạo với nhau góc
30
thì diện tích của thiết diện bằng:
A.
2
18cm
. B.
2
16cm
. C.
2
9cm
. D.
2
10cm
.
Câu 13. Cho tam giác
ABC
có
3AB =
,
5BC =
và
4AC =
. Cho tam giác
ABC
quay quanh
AB
và
AC
ta được hai hình nón có diện tích xung quanh là
1
S
và
2
S
. Chọn kết quả đúng?