S GIÁO D C VÀ ĐÀO T OỞ Ụ Ạ KI M TRA CH T L NG H C KỲ IỂ Ấ ƯỢ Ọ
Đ NG THÁPỒNăm h c: 2012-2013ọ
Môn thi: Toán – Kh i 12ố
Đ Đ XU TỀ Ề Ấ Th i gian: 90 phút (ờkhông k th i gian phát để ờ ề)
(Đ g m có 01 trang)ề ồ Ngày thi: 10/01/2012
Đ n v ra đ : THPT Lai vung 2ơ ị ề
I − PH N CHUNG CHO T T C H C SINH: (7,0 đi m)Ầ Ấ Ả Ọ ể
Câu I: (3 điêm) Cho ham sô
3 2
3 1y x x= − + −
co đô thi (C)
1). Khao sat s biên thiên va ve đô thi (C) cua ham sô trên. ư
2). D a vào đ th (C ) bi n luân s nghi m c a ph ng trình ự ồ ị ệ ố ệ ủ ươ
3 2
3 0x x m− + =
Câu II: (2 đi m ) ể
1.(1,0 đ ) Rút g n bi u th c sau: A= (2x+ọ ể ứ
2
y
)-1
( )
1
1
22
y
x
−
−
+
÷
;
0; 0x y≠ ≠
2.( 1,0 đ) Tìm giá tr l n nh t và giá tr nh nh t c a hàm sị ớ ấ ị ỏ ấ ủ ố
y= f(x)= x2 – ln(1-2x) trên đo n ạ
[ ]
2;0−
Câu III: (2 đ)
1.(1,0 đ ) Cho hình chóp S.ABCD có đáy ABCD là hình vuông có tâm là O. C nhạ
bên SA vuông góc v i m t ph ng đáy (ABCD). Bi t AB=2a và góc gi a c nh SO v iớ ặ ẳ ế ữ ạ ớ
m t đáy (ABCD) m t góc 60ặ ộ 0. Tính th tích kh i chóp S.ABCD theo aể ố
2. (1,0 đ) Cho hình nón đ nh S có đ ng sinh là a, góc gi a đ ng sinh và đáy là ỉ ườ ữ ườ
0
30
.
M t m t ph ng h p v i đáy m t góc 60ộ ặ ẳ ợ ớ ộ 0 và c t hình nón theo hai đ ng sinh SA vàắ ườ
SB. Tính di n tích tam giác SAB .ệ
II − PH N RIÊNG: (3,0 đi m),( Ầ ể H c sinh đ c ch n m t trong hai ph n)ọ ượ ọ ộ ầ
1. Theo ch ng trình chu n:ươ ẩ
Câu IVa: (1,0 đ) Cho hàm s ố
2 3
2 1
x
yx
+
=−
. Vi t ph ng trình ti p tuy n c a (C ) t iế ươ ế ế ủ ạ
giao đi m c a đ th (C ) v i tr c tung.ể ủ ồ ị ớ ụ
Câu Va: (2,0 điêm)
1. Gi i ph ng trình sau: ả ươ
2. Gi i b t ph ng trình sau: ả ấ ươ
2
4 2
1 3
log log 1 0
4x
x− − >
2.Theo ch ng trình nâng cao:ươ
Câu IVb: (1,0 đ) Cho hàm s ố
3
3 2y x x=−+
(C ). Vi t ph ng trình ti p tuy n c aế ươ ế ế ủ
( C), Bi t ph ng trình ti p tuy n có h s góc b ng 9.ế ươ ế ế ệ ố ằ
Câu Vb: (2,0 điêm)
1. Cho hàm s y= ố
12 2009
.
x
x e
. Ch ng minh r ngứ ằ :
. ' (12 2009 ) 0x y y x− + =
2. Cho hàm s ố
2 1
1
x
yx
−
=+
có đ th (C ) . Tìm m đ đ ng th ng d: ồ ị ể ườ ẳ
y x m= +
c tắ
(C ) t i hai đi m phân bi t A, B sao cho ạ ể ệ
2 2AB =
---H t---ế
G I Ý BÀI GI IỢ Ả
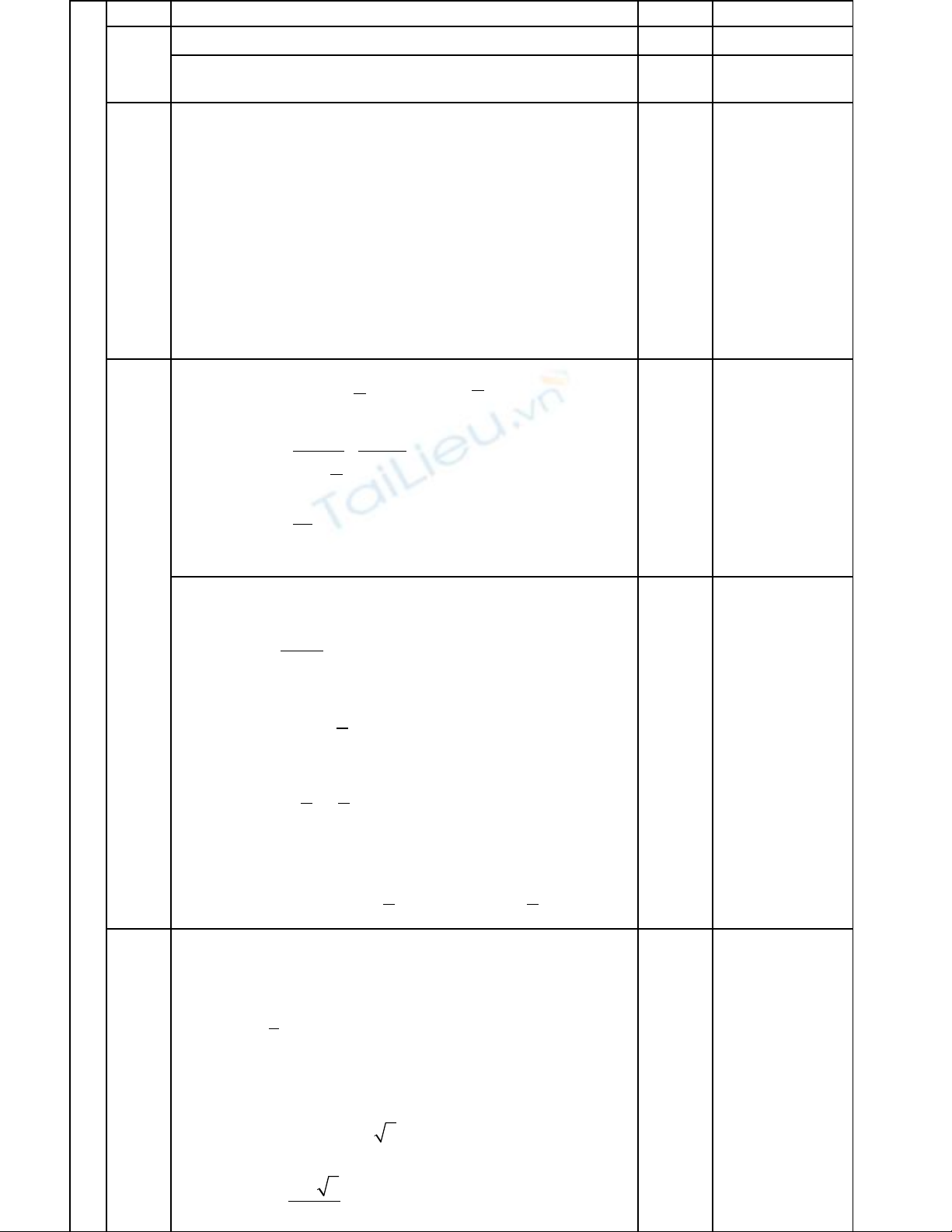
Ph n Chung : 7 đi mầ ể
Câu H ng D nướ ẫ Đi mểGhi Chú
Câu
1.1 1). Khao sat va ve đô thi ham sô:
3 2
3 1y x x= − + −
Câu
1.2
2) Bi n lu n:ệ ậ
3 2
3 0x x m− + =
(*)
3 2
3 1 1x x m⇔ − + − = −
S nghi m c a ph ng trình (*) b ng s giaoố ệ ủ ươ ằ ố
đi m c a đ th (C ) và đ ng th ng d:ể ủ ồ ị ườ ẳ
Ta có:
+
( ;0) (4; )m∈ −∞ ∪ +∞
: ph ng trình có m tươ ộ
nghi m.ệ
+
0
4
m
m
=
=
: ph ng trình có 2 nghi m.ươ ệ
+
(0;4)m∈
: ph ng trình có 3 nghi m.ươ ệ
Câu
2
1). Tinh A= (2x+
2
y
)-1
( )
1
1
22
y
x
−
−
+
÷
1 4
.( )
2
22
1
y x
yxy
x
xy
+
=+
=
2). y= f(x)= x2 – ln(1-2x) trên đo n ạ
[ ]
2;0−
+
2
' 2 1 2
y x x
= + −
+
1( )
' 0 1( )
2
x l
yx n
=
= ⇔ = −
+ Ta có:
( 2) 4 ln 5
1 1
( ) ln 2
2 4
(0) 0
y
y
y
− = −
− = −
=
V y GTLN c a y là 4-ln5 t i x=-2ậ ủ ạ
GTNN c a y là ủ
1ln 2
4−
t i x=ạ
1
2
−
1.
Ta có:
SA ( ABCD )⊥
⇒
1
3
SABCD ABCD
V SA.S=
mà
2
4
ABCD
S a=
( )ABCD
AO hc SO=
¼
0
60SOA⇒ =
0
60 6SA tan .AO a= =
* Th tích kh i chópể ố
3
4 6
3
S .ABCD
a
V=
2.