Đ s 5ề ố
Đ THI H C KÌ 1 – Năm h c 2007 – 2008Ề Ọ ọ
Môn TOÁN L p 11 – Nâng caoớ
Th i gian làm bài 90 phútờ
Bài 1: (1,5đ)
a) Tìm giá tr l n nh t và giá tr nh nh t c a hàm s ị ớ ấ ị ỏ ấ ủ ố
1 2sin 2 4
π
� �
= + +
� �
� �
y x
.
b) Xét tính ch n l c a hàm s ẵ ẻ ủ ố
( )
sin( ) sin( )
4 4
π π
= = − + +y f x x x
.
Bài 2: (2đ) Gi i các ph ng trình sau:ả ươ
a)
cos 2 3cos 2 0
− + =
x x
(1)
b)
+ − =3 cos 4 sin 4 2 cos 3 0x x x
(2)
Bài 3: (1,5đ)
Có 14 ng i g m 8 nam và 6 n , ch n ng u nhiên m t t 6 ng i. Tính:ườ ồ ữ ọ ẫ ộ ổ ườ
a) S cách ch n đ đ c m t t có nhi u nh t là 2 n .ố ọ ể ượ ộ ổ ề ấ ữ
b) Xác su t đ đ c m t t ch có 1 n .ấ ể ượ ộ ổ ỉ ữ
Bài 4: (2đ)
a) Ch ng mình r ng, v i ứ ằ ớ
3k n
, ta có:
1 2 3
3
3 3
k k k k k
n n n n n
C C C C C
− − − +
+ + + =
b) Cho đ ng tròn (C) tâm I(4; –5), bán kính R = 2. Tìm nh (C’) c a đ ng tròn (C) qua phép t nhườ ả ủ ườ ị
ti n theo véc t ế ơ
( )
1; 3v= −
r
.
Bài 5: (3đ)
Cho t di n ABCD, g i M và N l n l t là trung đi m c a các c nh AB và CD, trên c nh AD l yứ ệ ọ ầ ượ ể ủ ạ ạ ấ
đi m P không trùng v i trung đi m c a AD.ể ớ ể ủ
a) G i E là giao đi m c a đ ng th ng MP và đ ng th ng BD. Tìm giao tuy n c a hai m tọ ể ủ ườ ẳ ườ ẳ ế ủ ặ
ph ng (PMN) và (BCD).ẳ
b) Tìm thi t di n c a m t ph ng (PMN) v i t di n ABCD.ế ệ ủ ặ ẳ ớ ứ ệ
––––––––––––––––––––H t–––––––––––––––––––ế
H và tên thí sinhọ: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . SBD :. . . . . . . . . .
Đ s 5ề ố
ĐÁP ÁN Đ THI H C KÌ 1 – Năm h c 2007 – 2008Ề Ọ ọ
Môn TOÁN L p 11 – Nâng caoớ
Th i gian làm bài 90 phútờ
Bài 1
(1,5đ)
N i dungộĐi mể
Câu a
(0,75đ)
1 1 2 2 3 1 3
4
π
� �
− + + −� � � � � �
� �
� �
sin x y
V y: Maxy = 3 và miny = –1ậ
0,5
0,25
Câu b
(0,75đ)
T p xác đ nh D = ậ ị
ﾡ
x D x D
∀ −�� �
( )
( )
sin sin sin sin
4 4 4 4
sin sin sin sin
4 4 4 4
π π π π
π π π π
� � � �
� � � � � � � �
− = − − + − + = − + + − −
� � � � � � � �
� � � �
� � � � � � � �
� � � �
� �
� � � � � � � �
= − + − − = − + + − = −
� � � � � � � �
� �
� � � � � � � �
� �
f x x x x x
x x x x f x
V y f(x) là hàm s lậ ố ẻ
0,25
0,25
0,25
Bài 2
(2đ)
N i dungộĐi mể
Câu a
(1đ)
2
(1) 2cos 3cos 1 0− + =�x x
cos 1
cos 1
1cos os
cos 3
2
π
=
=
� �
=
=
x
x
x c
x
( )
2
2
3
π
ππ
=
� �
= +
x k
k Z
x k
0,25
0,5
0,25
Câu b
(1đ)
( )
� �
+ =�� �
� �
� �
3 1
2 2 cos 4 sin 4 2 cos 3
2 2
x x x
π
� �
− =�� �
� �
cos 4 cos 3
6
x x
ππ
ππ
− = +
− = − +
4 3 2
6
4 3 2
6
x x k
x x k
( )
ππ
π π
= +
� �
= +
2
6
2
42 7
x k
k Z
k
x
0,25
0,25
0,25
0,25
2
Bài 3
(1,5đ)
N i dungộĐi mể
Câu a
(0,75đ)
TH1: 0 n + 6 nam, s cách ch n là ữ ố ọ
0 6
6 8
C C
.
TH2: 1 n + 5 nam, s cách ch n là ữ ố ọ
1 5
6 8
C C
.
TH3: 2 n + 4 nam, s cách ch n là ữ ố ọ
2 4
6 8
C C
.
C 3 tr ng h p, s cách ch n là ả ườ ợ ố ọ
0 6 1 5 2 4
6 8 6 8 6 8
1414C C C C C C+ + =
0,5
0,25
Câu b
(0,75đ)
( )
6
14
3003
Ω = =
.n C
( )
1 5
6 8
336
= =
i A l bi n c : "Ch n c 6 n g i t ron� � � � � ��� �� g
ch c 1 n ", . .�� �� �
G
n A C C
( ) ( )
( )
336 16
3003 143
= = =
Ω.
n A
P A n
0,25
0,25
0,25
Bài 4
(2đ)
N i dungộĐi mể
Câu a
(1đ)
( ) ( ) ( )
− − − − −
= + + + + +
1 1 2 2 3
2
k k k k k k
n n n n n n
VT C C C C C C
− −
+ + +
= + +
1 2
1 1 1
2
k k k
n n n
C C C
( ) ( )
− − −
+ + + +
=+++
1 1 2
1 1 1 1
k k k k
n n n n
C C C C
−
+ + +
= + =
1
2 2 3
k k k
n n n
C C C
0,25
0,25
0,25
0,25
Câu b
(1đ)
Ph ng trình đ ng tròn (C): ươ ườ
( ) ( )
2 2
4 5 4x y− + + =
L y b t kỳ M(x; y) ấ ấ
( ) ( )
2 2
( ) 4 5 4C x y− + + =� �
(*)
( ) ( )
' 1 ' 1
' '; ' ' 3 ' 3
v
x x x x
T M M x y y y y y
= + = −
� �
=��
� �
= − = +
� �
r
( )
( ) ( ) ( ) ( ) ( )
− − + + + = − + + =� �
2 2 2 2
Th a y vﾡ o * :
* ' 1 4 ' 3 5 4 ' 5 ' 8 4x y x y
V y ph ng trình (C’): ậ ươ
( ) ( )
2 2
5 8 4x y− + + =
0,25
0,25
0,25
0,25
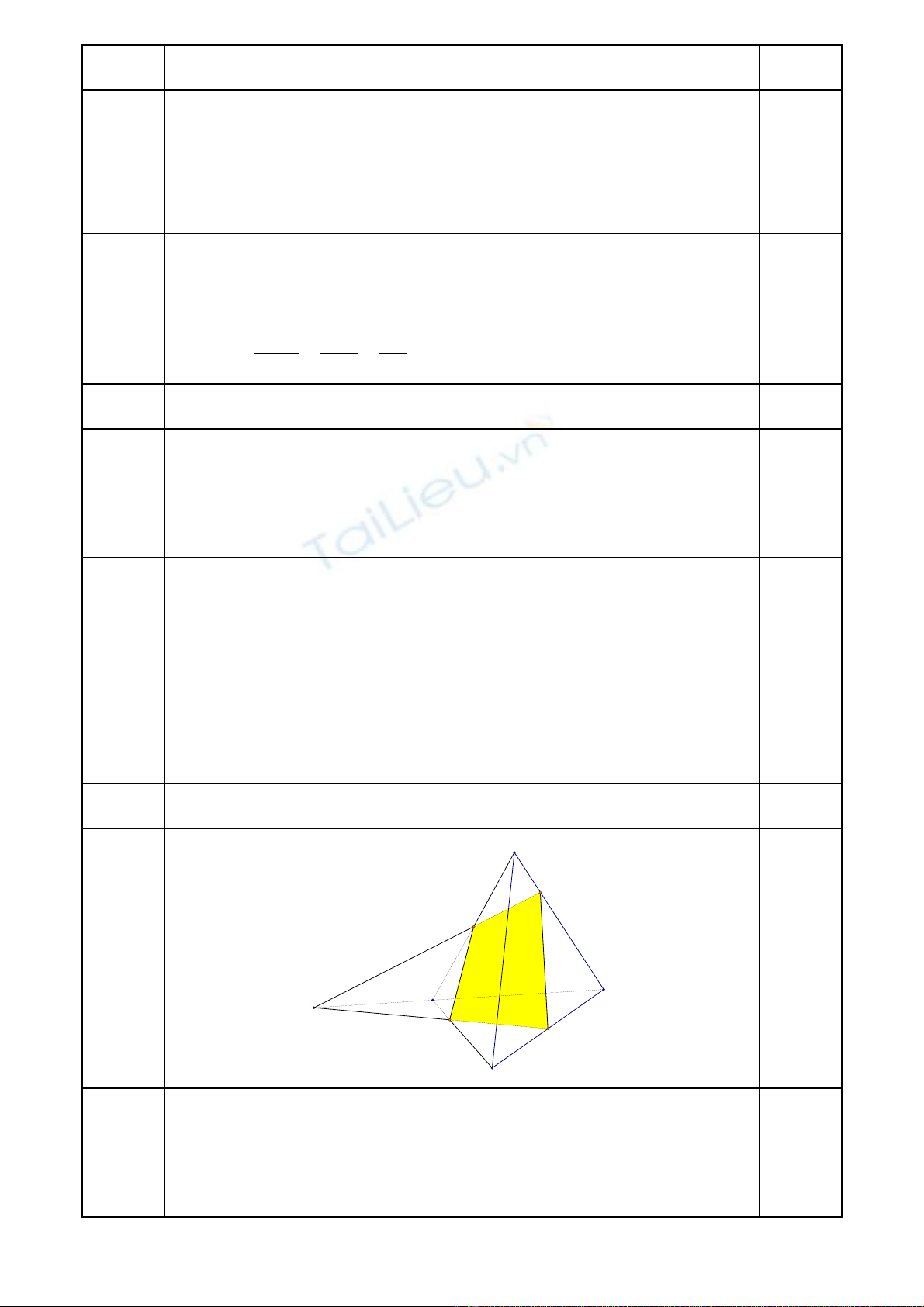
Bài 5
(3đ)
N i dungộĐi mể
F
E
N
M
B
D
C
A
P
0,5
Câu a
(1, 5đ)
( ) ( )
( ) ( )
,E M P B D su y ra
E MP MN P E MN P
E BD B CD E BCD
=
� � � �
� � � �
l i m ch ung t h nh t��� � �E
0,5
3
( )
( ) ( )
( ) ( )
� � � �
=� �l i m chu ng t h ha i. Suy r a ��� �
N MN P
N CD B CD N BCD
N MN P B CD EN
0,5
0,5
Câu b
(1đ)
( )
( ) ( ) ( ) ( )
( ) ( )
( ) ( )
( ) ( )
= =� � � � �
=�
=�
=�
Tr on g mp BCD g i F = EN BC�
DoE N
M t kh c:� �
PM N BC PM N F AB C PM N MF
BCD PMN FN
ACD PMN N P
AB D PMN PM
V y thi t di n c a mp(PMN) và t di n ABCD là t giác MFNP.ậ ế ệ ủ ứ ệ ứ
0,5
0,25
0,25
4