zunia.vn

Tuyển sinh 2024 dành cho Gen-Z

zunia.vn

» Tài Liệu Phổ Thông

» Đề thi - Kiểm tra

ĐỀ THI HỌC KÌ 1 Năm học 2009 – 2010 Môn TOÁN Lớp 11: Đề số 7

Chia sẻ: Trần Văn Thành | Ngày: | Loại File: DOC | Số trang:3

Báo xấu

113
lượt xem 13
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Câu 1: (4 điểm) 1) Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức y = sin2x - 3cos2x -1. 2) Giải các phương trình sau: a) 2sinx + 3= 0 b) 4sin2 x 23sin2x cos2 x 0 - - = c) x x x x sin ccooss2(7p ) 2(1 sin ) = + + + Câu 2: (3 điểm) 1) Trên một kệ sách có 12 quyển sách khác nhau, gồm 4 quyển tiểu thuyết, 6 quyển truyện tranh và 2 quyển truyện cổ tích. Lấy ngẫu nhiên 3 quyển từ kệ sách. a) Tính xác suất để lấy được 3 quyển đôi một khác loại. b)...

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: ĐỀ THI HỌC KÌ 1 Năm học 2009 – 2010 Môn TOÁN Lớp 11: Đề số 7

ĐỀ THI HỌC KÌ 1 – Năm học 2010 – 2011 Môn TOÁN Lớp 11 Nâng cao Đề số 7 Thời gian làm bài 120 phút Câu 1: (4 điểm) 1) Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức y = sin2x − 3cos2x − 1. 2) Giải các phương trình sau: cos2 x 3 2 2 b) 4sin x − sin2x − cos x = 0 = 2(1+ sin x ) a) 2sin x + 3 = 0 c) sin x + cos(7π + x ) 2 Câu 2: (3 điểm) 1) Trên một kệ sách có 12 quyển sách khác nhau, gồm 4 quyển ti ểu thuyết, 6 quyển truyện tranh và 2 quyển truyện cổ tích. Lấy ngẫu nhiên 3 quyển từ kệ sách. a) Tính xác suất để lấy được 3 quyển đôi một khác loại. b) Tính xác suất để lấy được 3 quyển trong đó có đúng 2 quyển cùng một loại. 5 � 2� 2) Tìm hệ số của số hạng chứa x trong khai triển P (x ) = �x 3 − �. 10 3 x2 � � Câu 3: (1,5 điểm) Trên đường tròn (O; R) lấy điểm A cố định và đi ểm B di đ ộng. G ọi I là trung đi ểm của AB. Tìm tập hợp các điểm K sao cho ∆ OIK đều. 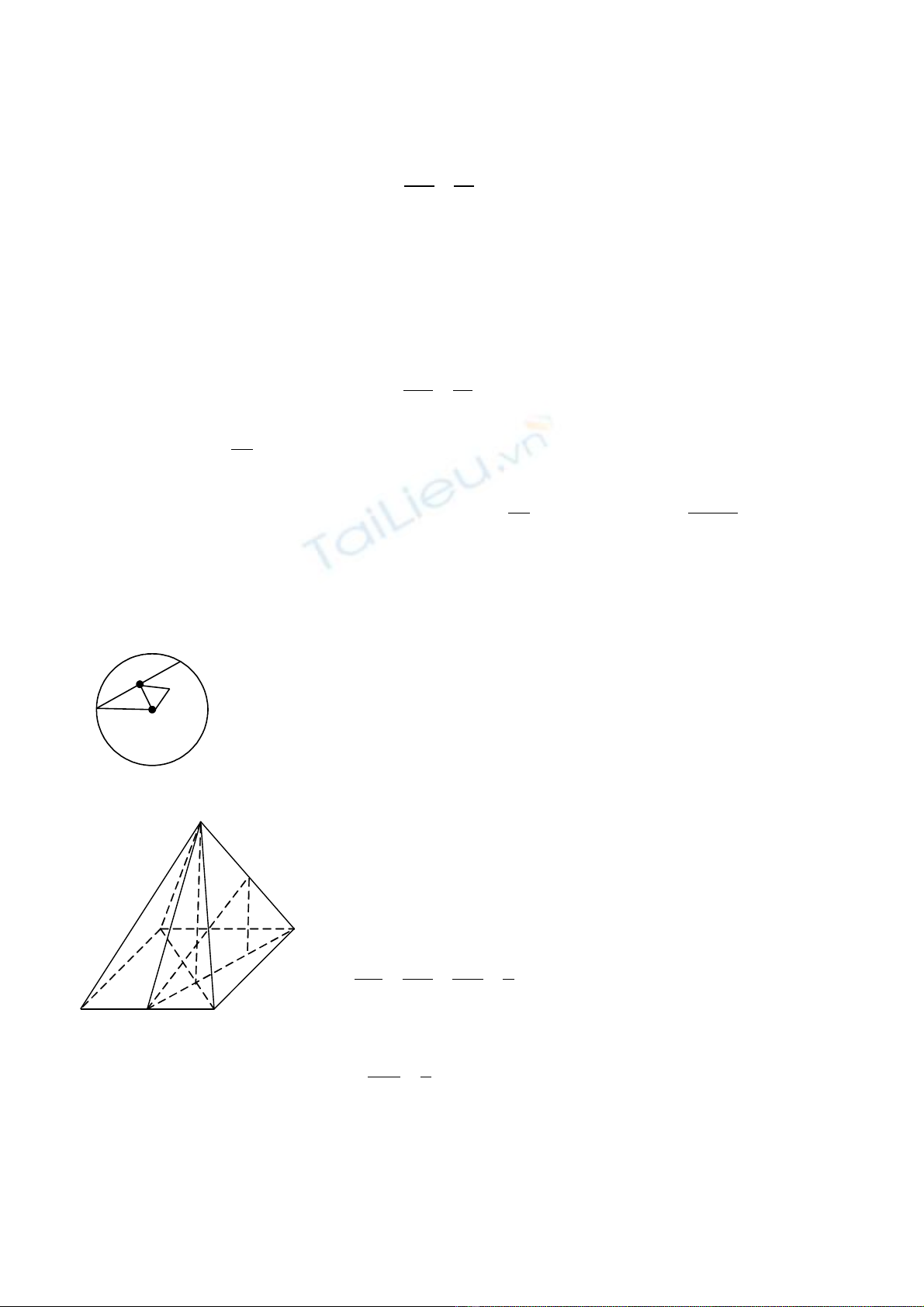Câu 4: (1,5 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. G ọi M, N l ần l ượt là trung điểm của AB và SC. 1) Tìm giao tuyến của (SMN) và (SBD). 2) Tìm giao điểm I của MN và (SBD). MI 3) Tính tỉ số . MN --------------------Hết------------------- Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . SBD :. . . . . . . . . . 1
ĐÁP ÁN ĐỀ THI HỌC KÌ 1 – Năm học 2010 – 2011 Môn TOÁN Lớp 11 Nâng cao Đề số 7 Thời gian làm bài 120 phút Câu 1: 1) Giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = sin2x − 3cos2x − 1 � � � π� 1 3 cos2x � 1 = 2sin� x − � 1 − 2 Ta có: y = sin2x − 3cos2x − 1 = 2� sin2x − − � 3� �2 2 � � π� ⇒ −3 y 1 (vì −1 sin� x − � 1) 2 � 3� π 5π ⇒ min y = −3 khi x = − + kπ ; max y = 1 khi x = + kπ . 12 12 2) Giải phương trình: π x = − + k 2π 3 3 a) 2sin x + 3 = 0 ⇔ sin x = − 4π 2 + k 2π x= 3 3 b) 4sin2 x − sin2x − cos2 x = 0 ⇔ 4sin2 x − 3sin x.cos x − cos2 x = 0 (*) 2 cos x = 0 thì (*) ⇔ sin x = 0 (vô lí) ⇒ cos x = 0 không thoả (*) + Với + Với cos x 0. Chia 2 vế của (*) cho cos2 x , ta được: π + kπ x= tan x = 1 4 2 (*) ⇔ 4tan x − 3tan x − 1= 0 ⇔ 1⇔ tan x = − � 1� x = arctan� � kπ −+ 4 � 4� π � 1� Vậy PT có nghiệm: x = + kπ ; x = arctan� � kπ −+ 4 � 4� cos2 x 1− sin2 x = 2(1+ sin x ) ⇔ = 2(1+ sin x ) c) (*) sin x + cos(7π + x ) sin x − cos x π mπ sin x −�۹+ 0 x Điều kiện: cos x (1) 4 sin x = −1 (2) Với điều kiện (1) thì (*) ⇔ (1+ sin x )(1− 3sin x + 2cos x ) = 0 ⇔ 3sin x − 2cos x = 1 (3) π + k 2π (thoả (1)) • (2) ⇔ x = − 2 3 2 1 1 2 3 ⇔ sin( x − α ) = (với sinα = ; cosα = sin x − cos x = • (3) ⇔ ) 13 13 13 13 13 13 1 1 x − α = arcsin + k 2π x = α + arcsin + k 2π 13 13 ⇔ ⇔ (thoả (1)) 1 1 x − α = π − arcsin + k 2π x = α + π − arcsin + k 2π 13 13 1 1 π Vậy PT có nghiệm: x = − + k 2π ; x = α + arcsin + k 2π ; x = α + π − arcsin + k 2π 2 13 13 2 3 (với sinα = ; cosα = ) 13 13 2
Câu 2: 1) Số cách chọn 3 quyển sách tè kệ sách: C12 = 220 ⇒ n(Ω ) = 220 . 3 a) Gọi A là biến cố "Lấy được 3 quyển sách đôi một khác loại" 111 Số cách chọn 3 quyển sách đôi một khác loại: C4.C6.C2 = 48 ⇒ n(A) = 48 . 48 12 = ⇒ Xác suất của biến cố A: P(A) = . 220 55 b) Gọi B là biến cố "Lấy được 3 quyển sách, trong đó có đúng 2 quyển cùng loại" 21 C4 .C8 = 48 + Số cách chọn có đúng 2 quyển tiểu thuyết: 21 C6 .C6 = 90 + Số cách chọn có đúng 2 quyển truyện tranh: 21 C2 .C10 = 10 + Số cách chọn có đúng 2 quyển cổ tích: ⇒ Số cách chọn có đúng 2 quyển cùng loại: 48 + 90 + 10 = 148 ⇒ n(B ) = 148 148 37 = ⇒ Xác suất của biến cố B: P(B) = . 220 55 5 � 2� 2) P (x ) = �x 3 − � 3 x2 � � k 15−3k � 2� kx Tk +1 = C5 (3x 3)5−k − � = (−1 k 35−k .2k C5 k Số hạng tổng quát thứ k + 1 là: ) �2 x 2k �x � Để số hạng chứa x10 thì 15− 3k − 2k = 10 ⇔ k = 1 Vậy hệ số của số hạng chứa x10 là: (−1)135−1.21C5 = −810. 1 Câu 3: + Ta có ﾷAIO = 1v ⇒ Tập hợp các điểm I là đường tròn (C) nhận AO làm đ ường B kính. I + Vì ∆ OIK đều nên phép quay Q(O ,600 ) : I a K hoặc Q(O ,−600) : I a K K A O Vậy tập hợp các điểm K là hai đường tròn (C ′ ) và (C′ ′ ) lần lượt là ảnh của (C) qua các phép quay Q(O ,600 ) và Q(O ,−600) . Câu 4: a) Giao tuyến của (SMN) và (SBD) S Ta có: S ∈ (SMN) ∩ (SBD) (1) Trong mp(ABCD), gọi E = MC ∩ BD ⇒ E ∈ (SMN) ∩ (SBD) (2) Từ (1) và (2) ⇒ (SMN) ∩ (SBD) = SE N b) Giao điểm của MN và (SBD) Trong mp(SMN), gọi I = MN ∩ SE ⇒ I = MN ∩ (SBD) D C c) Xét hai tam giác BME và DCE, ta có MB // DC I F EB EM BM 1 = = = ⇒ ED EC DC 2 E Gọi F là trung điểm của EC ⇒ NF // SE và E là trung điểm của MF A M B ⇒ IE là đường trung bình của ∆ MNF ⇒ I là trung điểm của MN MI 1 =. ⇒ MN 2 =========================== 3

CÓ THỂ BẠN MUỐN DOWNLOAD

THÔNG TIN

TRỢ GIÚP

HỖ TRỢ KHÁCH HÀNG

Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.