S Ở GD&ĐT H I D NGẢ ƯƠ KÌ THI CH N H C SINH GI I T NHỌ Ọ Ỏ Ỉ
L P 9 THCS NĂM H C 2012 – 2013Ớ Ọ
MÔN THI: TOÁN
Th i gian làm bài: 150 phút (không k th i gian giaoờ ể ờ
đ )ề
Ngày thi: 27/03/2013
( Đ thi g m có 01 trangề ồ )
Câu 1 (2,0 đi m):ể
a) Rút g n bi u th c: ọ ể ứ
()
2
A = x 50 x + 50 x + x 50− − −
v i ớ
x 50
b) Cho
x + 3 = 2
. Tính giá tr c a bi u th c: B = xị ủ ể ứ 5 – 3x4 – 3x3 + 6x2 – 20x + 2018
Câu 2 (2,0 đi m):ể
a) Gi i ph ng trình ả ươ
2 2
4x 3x
+ = 6
x 5x + 6 x 7x + 6− −
b) Gi¶i hÖ ph¬ng tr×nh sau:
x + y + 4 xy = 16
x + y = 10
Câu 3 (2,0 đi m):ể
a) V i a, b là các s nguyên. ớ ố Ch ng minh r ng n u ứ ằ ế
2 2
4a + 3ab 11b−
chia h t cho 5ế
thì
−
4 4
a b
chia h t cho 5.ế
b) Cho ph ng trình ươ
2
ax +bx+1 0
=
v i a, b là các s h u t . Tìm a, b bi tớ ố ữ ỉ ế
là nghi m c a ph ng trình. ệ ủ ươ
Câu 4 (3,0 đi m):ể
Cho 3 đi m A, B, C c đ nh n m trên m t đ ng th ng d (B n m gi a A và C).ể ố ị ằ ộ ườ ẳ ằ ữ
V đ ng tròn tâm O thay đ i nh ng luôn đi qua B và C (O không n m trên đ ngẽ ườ ổ ư ằ ườ
th ng d). K AM và AN là các ti p tuy n v i đ ng tròn tâm O t i M và N. G i I làẳ ẻ ế ế ớ ườ ạ ọ
trung đi m c a BC, AO c t MN t i H và c t đ ng tròn t i các đi m P và Q (P n mể ủ ắ ạ ắ ườ ạ ể ằ
gi a A và O), BC c t MN t i K. ữ ắ ạ
a) Ch ng minh 4 đi m O, M, N, I cùng n m trên m t đ ng tròn.ứ ể ằ ộ ườ
b) Ch ng minh đi m K c đ nh khi đ ng tròn tâm O thay đ i.ứ ể ố ị ườ ổ
c) G i D là trung đi m HQ, t H k đ ng th ng vuông góc v i MD c t đ ngọ ể ừ ẻ ườ ẳ ớ ắ ườ
th ng MP t i E. Ch ng minh P là trung đi m ME.ẳ ạ ứ ể
Câu 5 (1,0 đi m):ể
Cho
n
1
A = (2n +1) 2n 1
−
v i nớ
*
ﾥ
.
Ch ng minh r ng: ứ ằ
1 2 3 n
A + A + A +...+ A <1
.
------------- H T ------------Ế
H và tên thí sinh: ………………………………ọ ….. S báo danh …………….ố
Đ THI CHÍNH TH CỀ Ứ
Ch kí giám th 1 …………………..ữ ị Ch kí giám th 2 …………………..ữ ị
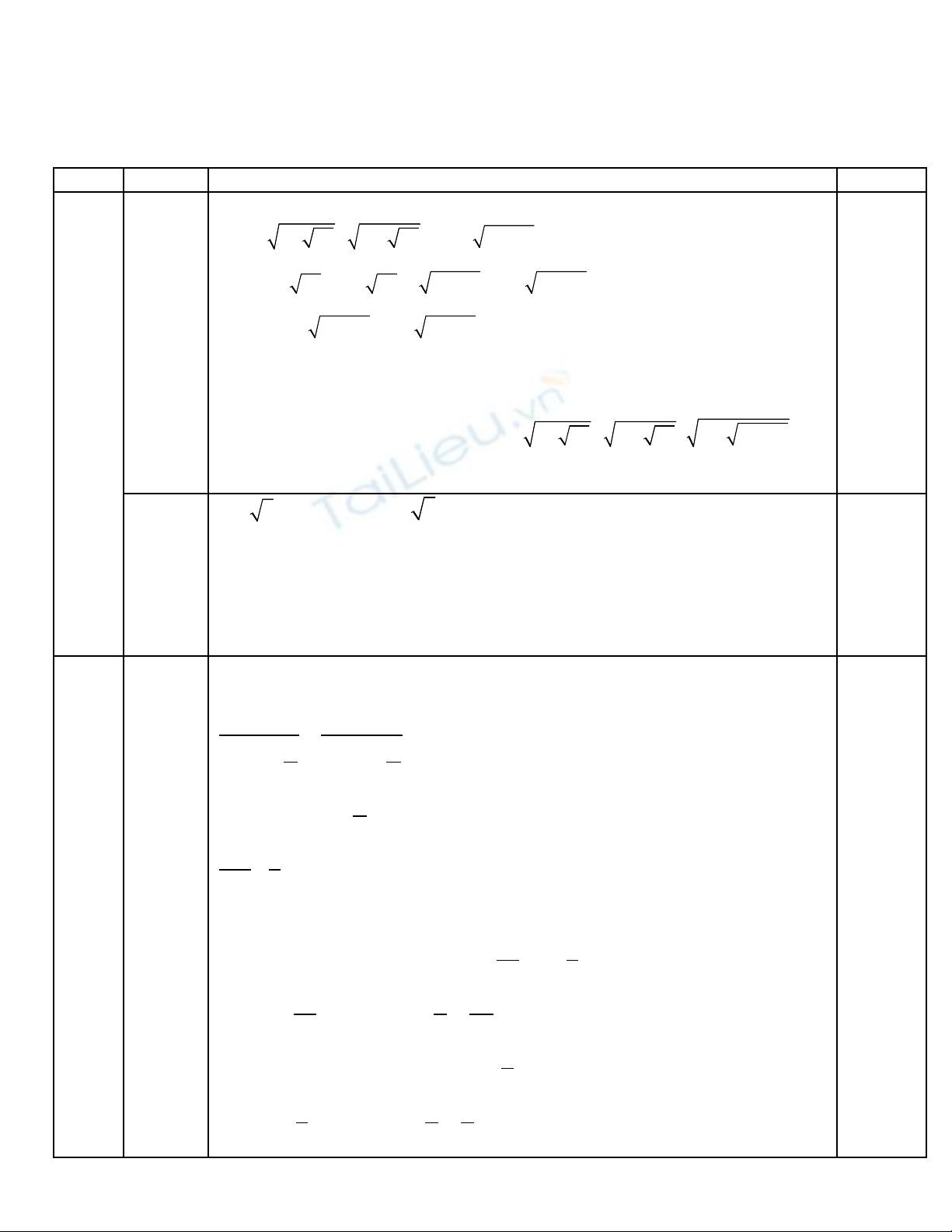
S Ở GD&ĐT H I D NGẢ ƯƠ ĐÁP ÁN VÀ H NG D N CH MƯỚ Ẫ Ấ
Đ THI H C SINH GI I T NHỀ Ọ Ỏ Ỉ
MÔN TOÁNL P 9 THCS NĂM H C 2012 – 2013Ớ Ọ
L u ýư: Thí sinh làm theo các khác đúng v n cho đi m t i đa. Đi m bài thi làm tròn đ n 0,25 đi mẫ ể ố ể ế ể
CÂU PH NẦN I DUNGỘĐI MỂ
Câu 1
2,0
đi mể
a)
1,0
đi mể
Ta có :
()
()
()()
()()
( )
2
2 2
2 2 2
2 2 2
2 2 2
2
A = x - 50 - x + 50 x + x -50
A = x - 50 + x + 50 - 2 x -50 x + x -50
A = 2x - 2 x -50 x + x -50
A = 2 x - x + 50
A = 100
Nh ng do theo gi thi t ta th y ư ả ế ấ
()
2
A = x - 50 - x + 50 x + x -50
<0
A= -10
0,25
0,25
0,25
0,25đ
b)
1,0
đi mể
x + 3 = 2
=>
2
2 3 ( 2) 3− = − − =�x x
2
4 1 0x x− + =�
B = x5 – 3x4 – 3x3 + 6x2 – 20x + 2018
B = (x5 – 4x4 + x3 ) + ( x4 – 4x3 + x2 ) + 5( x2 – 4x + 1) + 2013
B = x3( x2 – 4x + 1) +x2( x2 – 4x + 1) +5(x2 – 4x + 1) + 2013
B = 2013
0,25
0,25
0,25
0,25
Câu 2
2,0
đi mể
a)
1.0
đi mể
Nh n xét x = 0 không là nghi m c a ph ng trình ậ ệ ủ ươ
V i ớ
x 0
, ph ng trình đã cho t ng đ ng v i:ươ ươ ươ ớ
4 3
+ = 6
6 6
x 5 + x 7 +
x x
− −
Đ t ặ
6
t = x 7 + x
−
ph ng trình tr thànhươ ở
( ) ( )
( )
2 2
4 3
+ =6 1 t 0;t 2
t+2 t
1 4t 3t 6 6t 12t 6t 5t 6 0
−
+ + = + + − =� �
Gi i ph ng trình ta đ c ả ươ ượ
1 2
3 2
t ;t
2 3
−
= =
( th a mãn )ỏ
V i ớ
1
3
t2
−
=
ta có
2
6 3
7 2 11 12 0
2
x x x
x
−
− + = − + =�
Gi i ph ng trình ta đ c ả ươ ượ
1 2
3
x ;x 4
2
= =
( th a mãn )ỏ
V i ớ
2
2
t3
=
ta có
2
6 2
7 3 23 18 0
3
x x x
x
− + = − + =�
0,25
0,25
0,25
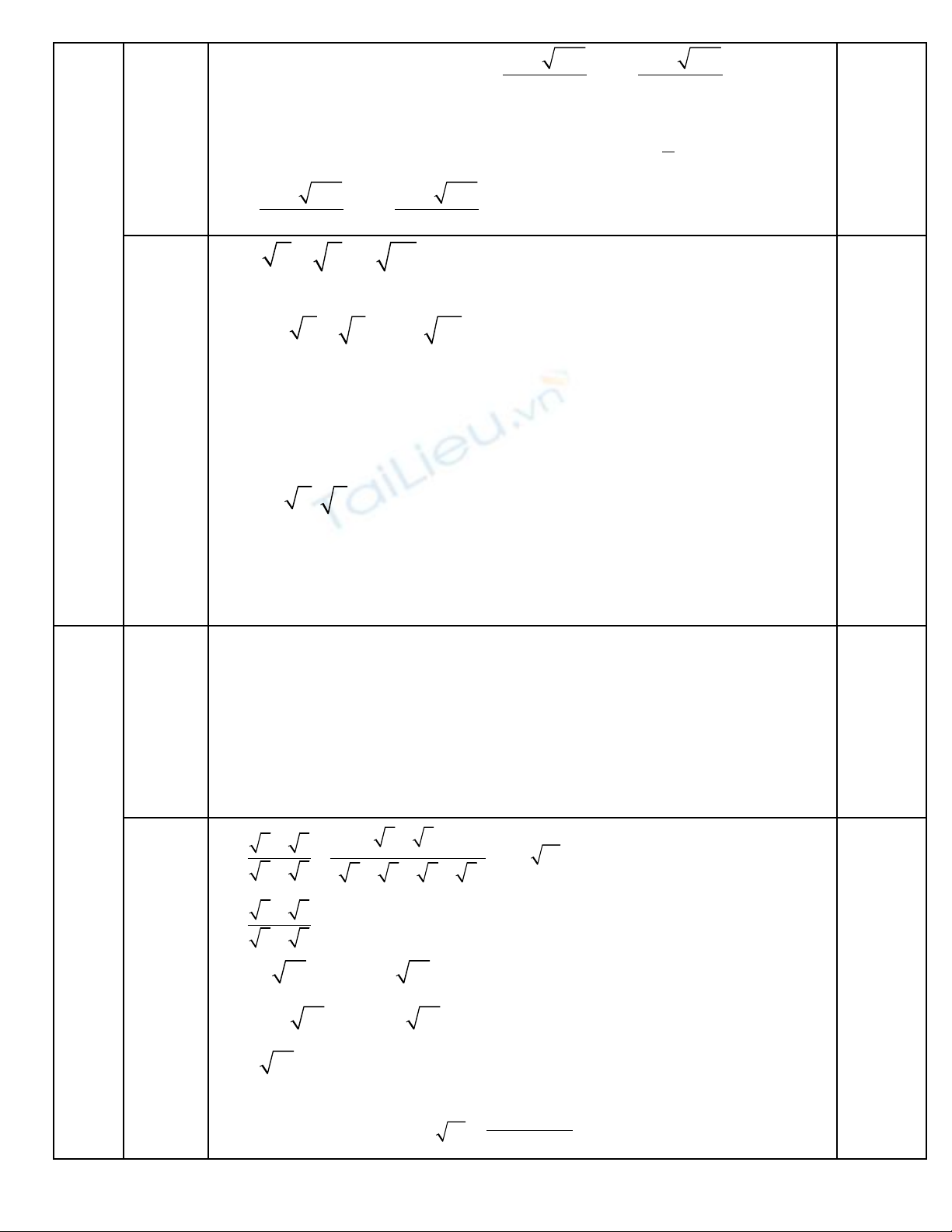
Gi i ph ng trình ta đ c ả ươ ượ
3 4
23 313 23 313
x ;x
6 6
+ −
= =
(th aỏ
mãn)
V y ph ng trình đã cho có b n nghi m là : ậ ươ ố ệ
1 2
3
x ;x 4
2
= =
;
3 4
23 313 23 313
x ;x
6 6
+ −
= =
0,25
b)
1,0
®iÓm
x + y + 4 xy = 16
x + y = 10
(I) (
x;y 0
)
Đ t S= ặ
x y+
; P =
xy
(
S 0;P 0
) h ệ(I) có d ngạ
2
S + 4P = 16
S - 2P = 10
( II)
Gi i h ( II) và đ i chi u đi u ki n ta đ c ả ệ ố ế ề ệ ượ
S = 4
P = 3
Khi đó
x; y
là 2 nghi m c a ph ng trình tệ ủ ươ 2 – 4t + 3 =0
Gi i ph ng trình ta đ c tả ươ ượ 1 = 3; t2 = 1
T đó suy ra h ph ng trình đã cho có hai nghi m ừ ệ ươ ệ
x = 9 x = 1
;
y = 1 y = 9
� �
� �
� �
0,25
0,25
0,25
0,25
Câu 3
2,0
đi mểa)
1.0
đi mể
( ) ( )
( )
+ − + − − + −�
+ +�
+�
M M
M
M
2 2 2 2 2 2
2 2
2
4a 3ab 11b 5 5a 5ab 10b 4a 3ab 11b 5
a 2ab b 5
a b 5
+�M a b 5
( Vì 5 là s nguyên t ) ố ố
( )
( ) ( )
4 4 2 2
a b a b a b a b 5
− = + + −�
M
0.25
0,25
0,25
0,25
b)
1,0
®iÓm
5 3
5 3
x−
=+
=
( )
( ) ( )
2
5 3 4 15
5 3 5 3
−= −
+ −
5 3
5 3
x−
=+
là nghi m c a ph ng trình nên ta cóệ ủ ươ
( ) ( )
( ) ( )
2
4 15 4 15 1 0
31 8 15 4 15 1 0
15(8 ) 31 4 1 0
a b
a b
a b a b
− + − + =
− + − + =
− + + + + =�
Vì
,a b Q
nên
(8 ), (31 4 1)a b a b Q+ + +
Do đó n u ế
8 0a b+
thì
15
31 4 1
8
a b Q
a b
+ +
=
+
(Vô lí)
0,25
0,25
0,25đ
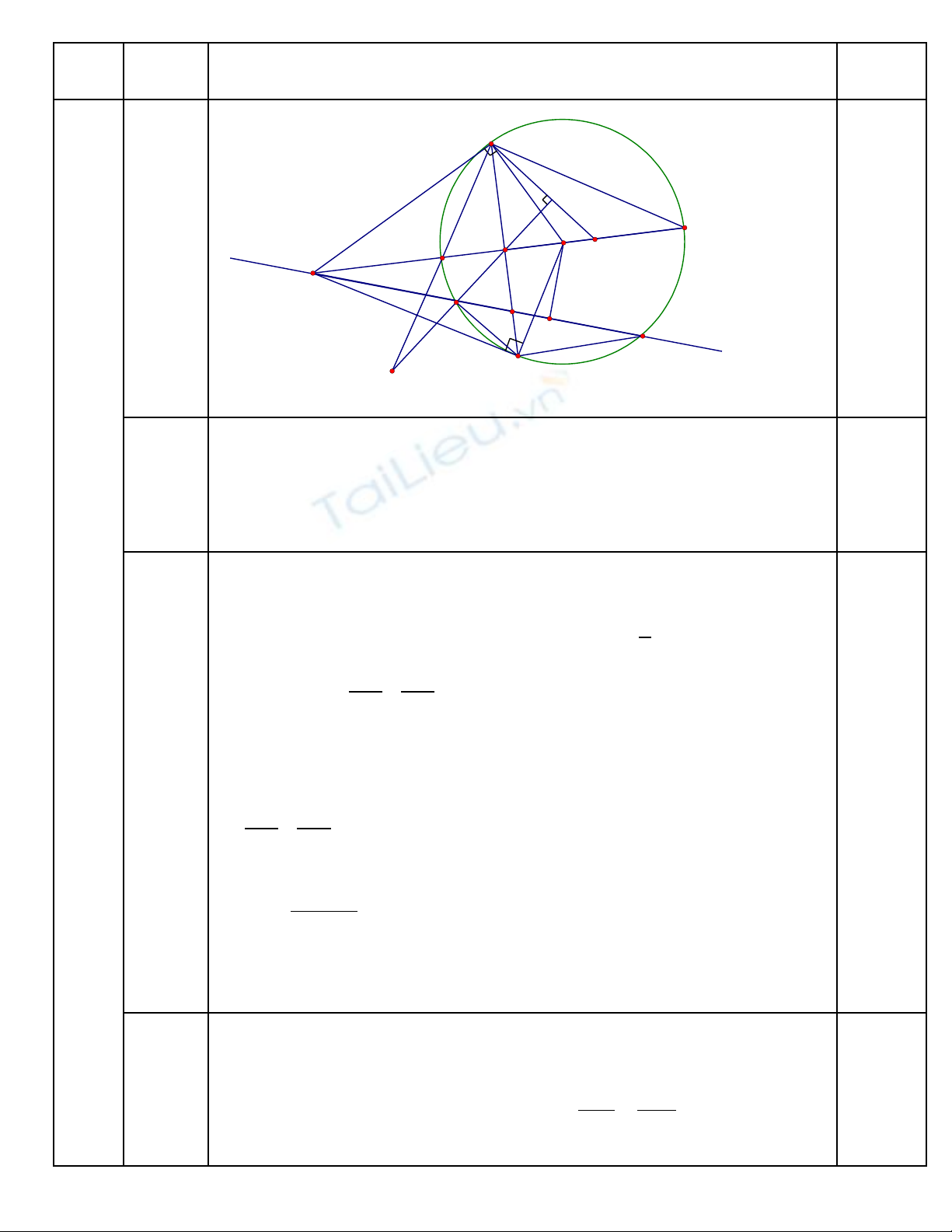
Suy ra
8 0 1
31 4 1 0 8
a b a
a b b
+ = =
� �
� �
+ + = = −
� �
0,25
Câu 4
3,0
đi mể
d
K
E
D
A
B
C
M
N
P
Q
I
H
O
a)
1,0
®iÓm
I là trung đi m c a BC ( dây BC không đi qua O )ể ủ
ﾥ
0
90OI BC OIA⊥ =� �
Ta có
ﾥ
0
90AMO =
( do AM là hai ti p tuy n (O) )ế ế
ﾥ
0
90ANO =
( do AN là hai ti p tuy n (O) )ế ế
Suy ra 4 đi m O, M, N, I cùng thu c đ ng tròn đ ng kính OAể ộ ườ ườ
0,25
0,25
0,25
0.25
b)
1,0
®iÓm
AM, AN là hai ti p tuy n (O) c t nhau t i A nên OA là tia phân giácế ế ắ ạ
ﾥ
MON
mà ∆OMN cân t i O nên ạ
OA MN⊥
∆ABN đ ng d ng v i ∆ANC ( vì ồ ạ ớ
ﾥ
ﾥ
1
ANB=ACN= 2
sđ
ﾥ
NB
và
ﾥ
CAN
chung ) suy ra
2
AB AN
= AB.AC=AN
AN AC
∆ANO vuông t i N đ ng cao NH nên ta có AH.AO = ANạ ườ 2
Suy ra AB.AC = AH.AO
∆AHK đ ng d ng v i ∆AIO ( vì ồ ạ ớ
ﾥ
ﾥ
0
AHK=AIO=90
và
ﾥ
OAI
chung )
AH AK
= AI.AK=AH.AO
AI AO
AI.AK=AB.AC
� �
AB.AC
AK= AI
Ta có A,B,C c đ nh nên I c đ nh suy ra AK c đ nh mà A c đ nh,ố ị ố ị ố ị ố ị
K là giao đi m c a dây BC và dây MN nên K thu c tia AB suy ra Kể ủ ộ
c đ nhố ị
0,25
0,25
0,25
0,25
c)
1,0
®iÓm
Ta có
ﾥ
0
PMQ=90
( góc n i ti p ch n n a đ ng tròn ).ộ ế ắ ử ườ
Xét ∆MHE và ∆QDM có
ﾥ
ﾥ
MEH=DMQ
( cùng ph v i ụ ớ
ﾥ
DMP
),
ﾥ
ﾥ
EMH=MQD
( cùng ph v i ụ ớ
ﾥ
MPO
)
ME MH
MQ DQ
=�
∆PMH đ ng d ng v i ∆MQH ồ ạ ớ
0,25