
S GIÁO D C & ĐÀOỞ Ụ
T OẠ
AN GIANG
K THI CH N H C SINH GI I C P T NHỲ Ọ Ọ Ỏ Ấ Ỉ
NĂM H C 2011-2012Ọ
MÔN: V T LÝ - 12Ậ
Th i gian:ờ 180 phút (không k th i gian giao đ)ể ờ ề
(Đ thi g m 2 trang)ề ồ
Bài 1: ( 2 đi mể)
Cho 3 dao đng đi u hòa, cùng ph ng, cùng t n s góc ộ ề ươ ầ ố = 100 rad/s v i các ớ
biên đ : Aộ1 = 1,5cm; A2 =
3
2
cm; A3 =
3
cm, các pha ban đu t ng ng ầ ươ ứ 1 = 0 ;
2
2
π
ϕ
=
;
3
5
6
π
ϕ
=
. Vi t ph ng trình dao đng t ng h p c a 3 dao đng trên.ế ươ ộ ổ ợ ủ ộ
Bài 2 (4 đi mể): M t ngu n đi n có su t đi n đng E, đi n tr trong r, c p đi n choộ ồ ệ ấ ệ ộ ệ ở ấ ệ
m t m ch ngoài có đi n tr R thay đi đc .ộ ạ ệ ở ổ ượ
1) a) Xác đnh R đ m ch ngoài tiêu th công su t c c đi . ị ể ạ ụ ấ ự ạ
b)Tìm bi u th c công su t c c đi và tính hi u su t c a ngu n đi n khi đó.ể ứ ấ ự ạ ệ ấ ủ ồ ệ
2) a)Ch ng minh v i m t giá tr công su t m ch ngoài P < Pứ ớ ộ ị ấ ạ max thì có hai giá tr c a Rị ủ
và hai giá tr đó tho mãn h th c : Rị ả ệ ứ 1.R2 = r2 .
b) Hi u su t c a ngu n đi n ng v i hai giá tr trên liên h v i nhau th nào ?ệ ấ ủ ồ ệ ứ ớ ị ệ ớ ế
Bài 3 ( 4 đi m)ể Đt v t sáng AB trên và vuông góc v i tr c chính c a th u kính h iặ ậ ở ớ ụ ủ ấ ộ
t Lụ1 có tiêu c 20cm. V t AB cách th u kính m t kho ng 30cm.ự ậ ấ ộ ả
a) Xác đnh v trí, tính ch t và s phóng đi nh Aị ị ấ ố ạ ả 1B1 v t AB cho b i th u kính ậ ở ấ
L1.
b) Gi nguyên v trí v t AB và Lữ ị ậ 1, ng i ta đt thêm m t th u kính phân kì Lườ ặ ộ ấ 2,
đng tr c chính v i Lồ ụ ớ 1 và cách L1 m t ộkho ng 70cm. Tính tiêu c c a th u kính ả ự ủ ấ
L2 đ nh cu i cùng Aể ả ố 2B2 c a v t AB qua h ( Lủ ậ ệ 1, L2) cao b ng v t AB. V ằ ậ ẽ
nh.ả
Bài 4 (4 đi mể): M ch đi n có s đ nh hình v . ạ ệ ơ ồ ư ẽ
Trang
1
Đ CHÍNH Ề
TH CỨ
A
R
D
L C
B E
f=50Hz
~
U=100V
Cu n dây thu n c m L. Ng i ta thay đi L và C đ ộ ầ ả ườ ổ ể
công su t m ch tuân theo bi u th c: ấ ạ ể ứ
2.
L C
P K Z Z=
.
a)Khi
1( )L H
π
=
thì
24K=
, dòng đi n trong m ch c c đi. Tính C và R.ệ ạ ự ạ
b)Tính đ l ch pha gi a uộ ệ ữ AE và uBD khi Imax. Tìm liên h gi a R, C, L đ I = K. Lúc đó ệ ữ ể
đ l ch pha gi a uộ ệ ữ AE và uBD b ng bao nhiêu?ằ
Bài 5 (2 đi mể): M t v t dao đng đi u hoà, lúc v t v trí M có to đ xộ ậ ộ ề ậ ở ị ạ ộ 1 = 3cm thì
v n t c là 8(cm/s); lúc v t v trí N có to đ xậ ố ậ ở ị ạ ộ 2 = 4cm thì có v n t c là 6(cm/s). Tínhậ ố
biên đ dao đng và chu k dao đng c a v t.ộ ộ ỳ ộ ủ ậ
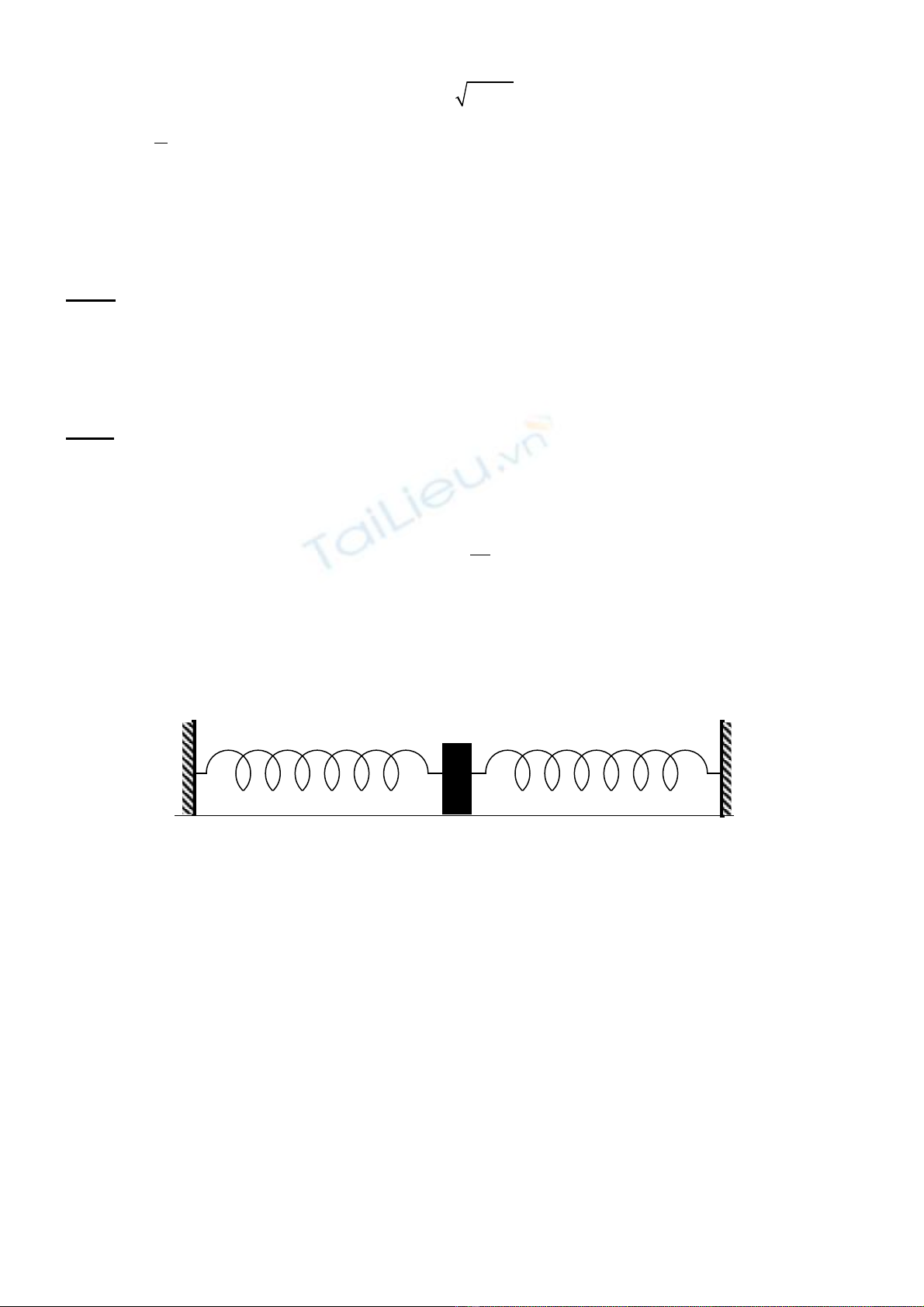
Bài 6 (4 đi mể):M t v t có kh i l ng m = 0,5kg đc g n vào v i hai lò xo có đ c ngộ ậ ố ượ ượ ắ ớ ộ ứ
K1, K2 nh hình v . . Hia lò xo có cùng chi u dài ư ẽ ề lo = 80cm và K1 = 3 K2. Kho ng cách ả
MN = 160 cm. Kéo v t theo ph ng MN t i v trí cách Mm t đo n 76cm r th nh ậ ươ ớ ị ộ ạ ồ ả ẹ
cho v t dao đng đi u hòa. Sau th i gian t = ậ ộ ề ờ
30
π
(s) k t lúc buông ra, v t đi đc ể ừ ậ ượ
quãng đng dai 6cm. ườ
Tính K1 và K2 . B qua m i mát và kh i l ng các lò xo, kích th c c ae v t. ỏ ọ ố ượ ướ ủ ậ
Cho bi t đ c ng c a h lò xo là Kế ộ ứ ủ ệ = K1 + K2.
………………….H t…………………….ế
Trang
2
0
K1K2
m
NM

S GIÁO D C & ĐÀO T OỞ Ụ Ạ
AN GIANG
K THI CH N H C SINH GI I C P T NHỲ Ọ Ọ Ỏ Ấ Ỉ
NĂM H C 2011-2012Ọ
MÔN: V T LÝẬ
Th i gian:ờ 180 phút (Không k th i gian giao đ)ể ờ ề
ĐÁP ÁN VÀ BI U ĐI MỂ Ể
Bài H NG D N CH MƯỚ Ẫ Ấ Điể
m
Bài 1:
Bài 2:
Trang
1
(2 đi m)ể
A12 =
2 2
1 2 1 2 2 1
2A A os( ) 3A A c
ϕ ϕ
+ + − =
cm 0,5
12 12
1
6
3
tg
π
ϕ ϕ
= =�
0,25
A =
2 2
12 3 12 3 2 1
2A A os( ) 3A A c
ϕ ϕ
+ + − =
cm. 0,5
12 12 3 3
12 12 3 3
sin sin
os os 2
A A
tg A c A c
ϕ ϕ π
ϕ ϕ
ϕ ϕ
+
= =�
+
0,5
X =
3
cos(100
2
t
π
ϕ
+
)cm 0,25
3
Đ CHÍNH TH CỀ Ứ

i
L
U
uur
C
U
uuur
AE
U
uuuur
BD
U
uuuur
R
U
uuur
O
2
ϕ
1
ϕ
Trang
2
(4
đi m)ể
1) a)+ Ta có :
E
IR r
=+
; P = R.I2 0,5
+ Suy ra : P =
2
2
)(
.
rR
RE
=
2
2
)( R
r
R
E
. 0,25
+Áp d ng h qu b t đng th c Côsi, suy ra Pụ ệ ả ấ ẳ ứ max khi: R = r
(1)
0,25
b)+Khi đó:
2
ax
4
m
E
Pr
=
(2)
0,25
+Hi u su t c a ngu n: ệ ấ ủ ồ
.
.
U I R
HE I R r
= = +
0,25
+Khi R = r thì
150%
2
H
= =
0,25
2)a)+T ừ
22 2 2
2
.. (2 ) 0
( )
E R
P P R rP E R r P
R r
= + − + =� �
+
(3)
0,25
+V i ớ
2 2
( 4 )E E rP∆ = −
(4)
. Thay
2
E
t (2) vào (4), đc:ừ ượ
2ax
.4 ( ) 0
m
E r P P
∆ = −
f
0,25
+Suy ra ph ng trình (3) có 2 nghi m riêng bi t:ươ ệ ệ
2 2
1
2 4
2
E rP E E rP
RP
− − −
=
(5)
;
2 2
2
2 4
2
E rP E E rP
RP
− + −
=
(6)
0,25
+L y (5) nhân (6) theo v , đc: ấ ế ượ
2
1 2
.R R r
=
(Đpcm)0,5
b) +V i Rớ1, có:
1 1
1
11 1 2
.
R R
HR r R R R
= =
++
(7)
+ V i Rớ2, có:
2 2
2
22 1 2
.
R R
HR r R R R
= =
++
(8)
0,25
0,25
+L y (7) + (8) theo v , đc: ấ ế ượ
1 2
1 100%H H+ = =
0,5
Bài 3
( 4 đi m)ể
a)
ta có : d’1 =
1
1
d f
d f
+
= 60cm. 0,5
d’1 > 0 nh là nh th t.Ả ả ậ 0.5
K1 = -
'
1
1
d
d
= - 2 0,5
b)
- Tính đc dượ 2 = l - d’1 = 10cm.
0,5
- Tính đc kượ 2 = 0,5 0,5
- Tính đc dượ 2’ = - 5cm. 0,5
- Tính f2 = -10cm 0,5
- V hình đúngẽ0,5
a)+ Ta có :
1
.2 . 2 50 100
L
Z L f
π π
π
= = = ��
0,25
+ Khi
2
4 4
L C
K P Z Z= =� �
(1) 0,25
+ Vì m ch RLC n i ti p có Iạ ố ế max nên c ng h ng x y ra ộ ưở ả
100
L C
Z Z= = Ω�
(2)
Do đó :
4
1 1 10 ( )
100 100
C
C F
Z
ω π π
−
= = =
� �
0,5
+T (1) và (2), đcừ ượ :
4 400(W)
L
P Z= =
0,25
+ M t khácặ :
2
P R I
=
, v i ớ
ax
min
R
m
U U
I I Z
= = =
nên
4

Bài 5: ( 2 đi m)ể
- Ghi chú:
- Thí sinh lu n gi i theo các cách khác, n u đúng v n đt đi m t i đa theo bi u đi m.ậ ả ế ẫ ạ ể ố ể ể
---------------------H tế…………………
Trang
5
(2
đi m)ể
+ Áp d ng h th c đc l p: ụ ệ ứ ộ ậ
2
2
2
v
A x
ω
= +
, đc:ượ 0,25
+T i M: ạ
1
1
2 2
2 2
2 2
8
3
v
A x
ω ω
= + = +
(1) 0,5
+T i N: ạ
2
2
2 2
2
22 2
6
4
v
A x
ω ω
= + = +
(2) 0,5
+Gi i h (1) và (2) đc:ả ệ ượ
A = 5 cm và
2 2
2( / ) 3,14( )
2
rad s T s
π π
ω π
ω
= = = = =�
0,75
Bài 4
( 4
đi m )ể
L c thu t l i đáp ánượ ậ ạ
L p lu n tính tính đc biên đ A = 4cm ậ ậ ượ ộ 1 đ
Xác đnh đc th i gian là t = ị ượ ờ
3
T
1 đ
Tính đc Chu Kì T = ượ
10
π
0,5đ
Tính đc ượ
20( d/s)ra
ω
=
0,5đ
Gi i h : Kả ệ 1 = 150N/m ; K2 = 50N/m 1d
5


























