UBND T NH THÁI NGUYÊNỈ
S GD&ĐTỞC NG HÒA XÃ H I CH NGHĨA VI T NAMỘ Ộ Ủ Ệ
Đc l p - T do - H nh phúcộ ậ ự ạ
K THI CH N H C SINH GI I C P T NH Ỳ Ọ Ọ Ỏ Ấ Ỉ
L P 12Ớ - MÔN: V T LÍ – Năm h c 2010 - 2011Ậ ọ
Th i gian: 180 phút - (Không k th i gian giao đ)ờ ể ờ ề
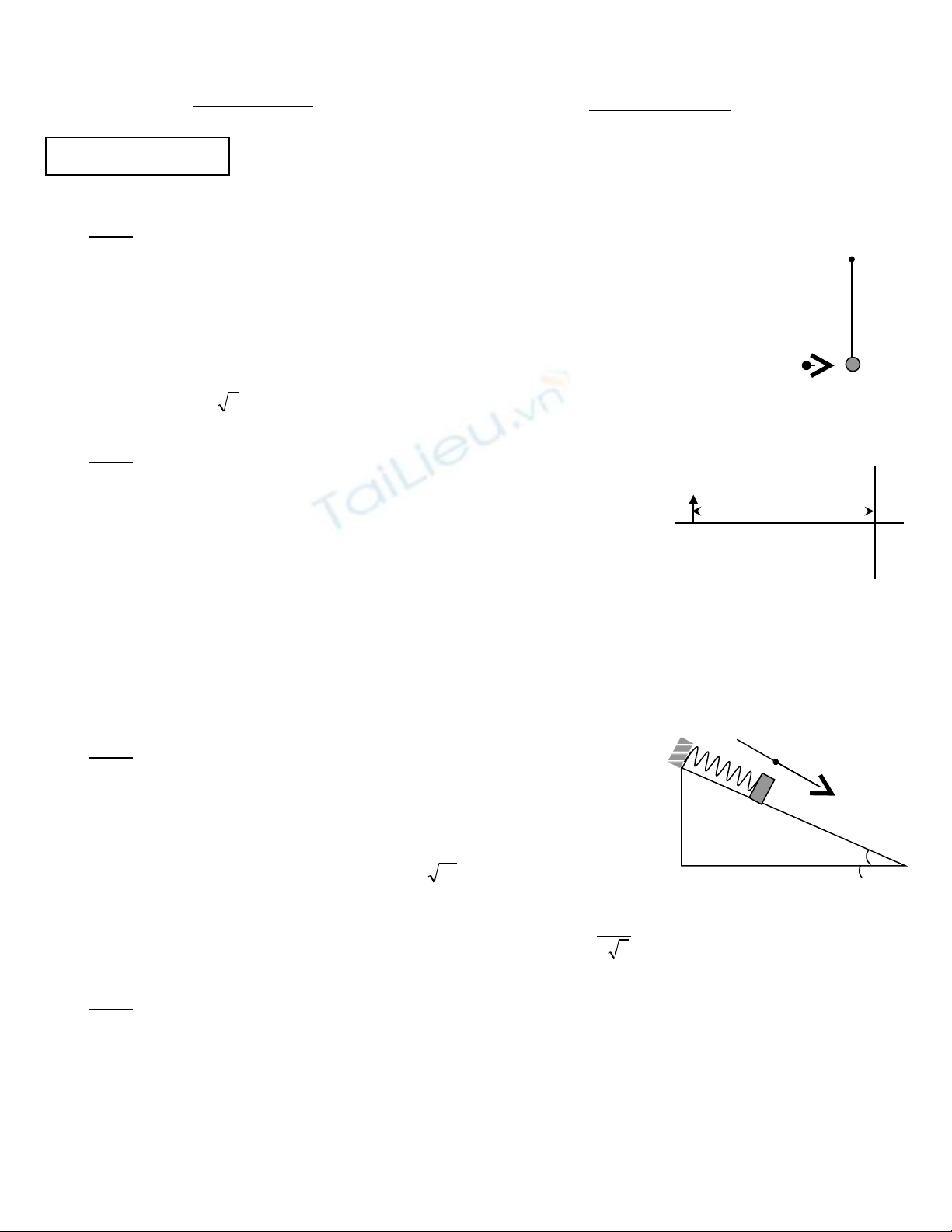
Bài 1
M t v t nh kh i l ng M =100g treo vào đu s i dây lí t ng, chi uộ ậ ỏ ố ượ ầ ợ ưở ề
dài l = 20cm nh Hình 1. Dùng v t nh m = 50g có t c đ vư ậ ỏ ố ộ 0 b n vào M. Bắ ỏ
qua s c c n c a không khí. L y g = 10m/sứ ả ủ ấ 2. Coi va ch m là tuy t đi đànạ ệ ố
h i.ồ
a/ Xác đnh vị0 đ M lên đn v trí dây n m ngang.ể ế ị ằ
b/ Xác đnh vị0 t i thi u đ M chuy n đng tròn xung quanh O.ố ể ể ể ộ
c/ Cho v0 =
2
73
m/s, xác đnh chuy n đng c a M.ị ể ộ ủ Hình 1
Bài 2
M t v t sáng AB hình mũi tên đt song song v i m t màn E nhộ ậ ặ ớ ộ ư
hình bên. Kho ng cách gi a AB và E là L. Gi a AB và E có m tả ữ ữ ộ
th u kính h i t tiêu c f. T nh ti n th u kính d c theo tr c chínhấ ộ ụ ự ị ế ấ ọ ụ
AE ng i ta th y có hai v trí c a th u kính đu cho nh rõ nét c aườ ấ ị ủ ấ ề ả ủ
AB trên màn.
a/ Tìm đi u ki n c a L đ bài toán th a mãn.ề ệ ủ ể ỏ
b/ Bi t kho ng cách gi a hai v trí c a th u kính là a. Tìm tiêu c f c a th u kính theo L và a.ế ả ữ ị ủ ấ ự ủ ấ
Áp d ng b ng s L = 90cm, a = 30cm.ụ ằ ố
c/ V n th u kính và màn E nh trên, thay AB b ng đi m sáng S đt trên tr c chính c a th uẫ ấ ư ằ ể ặ ụ ủ ấ
kính và cách E m t kho ng 45cm. Xác đnh v trí đt th u kính đ trên màn thu đc vùng sángộ ả ị ị ặ ấ ể ượ
có kích th c nh nh t.ướ ỏ ấ
Bài 3
Con l c lò xo nh hình v . V t nh kh i l ng m = 200g, lò xoắ ư ẽ ậ ỏ ố ượ
lí t ng có đ c ng k = 1N/cm, góc = 30αưở ộ ứ 0. L y g = 10m/sấ2.
a/ Ch n tr c t a đ nh hình v , g c t a đ trùng v i v trí cânọ ụ ọ ộ ư ẽ ố ọ ộ ớ ị
b ng. Vi t ph ng trình dao đng. Bi t t i th i đi m ban đu lòằ ế ươ ộ ế ạ ờ ể ầ
xo b dãn 2cm và v t có v n t c vị ậ ậ ố 0 = 10
15
cm/s h ng theo chi uướ ề
d ng.ươ
b/ T i th i đi m tạ ờ ể 1 lò xo không bi n d ng. H i t i tế ạ ỏ ạ 2 = t1 +
54
s, v t có t a đ bao nhiêu?ậ ọ ộ
c/ Tính t c đ trung bình c a m trong kho ng th i gian Δt = tố ộ ủ ả ờ 2 - t1.
Bài 4
Hai mũi nh n Sọ1, S2 ban đu cách nhau 8cm g n đu m t c n rung có t n s f = 100Hz,ầ ắ ở ầ ộ ầ ầ ố
đc đt ch m nh vào m t n c. T c đ truy n sóng trên m t n c là v = 0,8 m/s. ượ ặ ạ ẹ ặ ướ ố ộ ề ặ ướ
a/ Gõ nh c n rung cho hai đi m Sẹ ầ ể 1, S2 dao đng theo ph ng th ng đng v i ph ng trìnhộ ươ ẳ ứ ớ ươ
d ng u = A.cos2 ft. Vi t ph ng trình dao đng c a đi m Mπạ ế ươ ộ ủ ể 1 cách đu Sề1, S2 m t kho ng d =ộ ả
8cm.
b/ Tìm trên đng trung tr c c a Sườ ự ủ 1, S2 đi m Mể2 g n Mầ1 nh t và dao đng cùng pha v i Mấ ộ ớ 1.
Đ CHÍNH TH CỀ Ứ
v0
O
M
m
l
A
B
E
L
mx
α
O
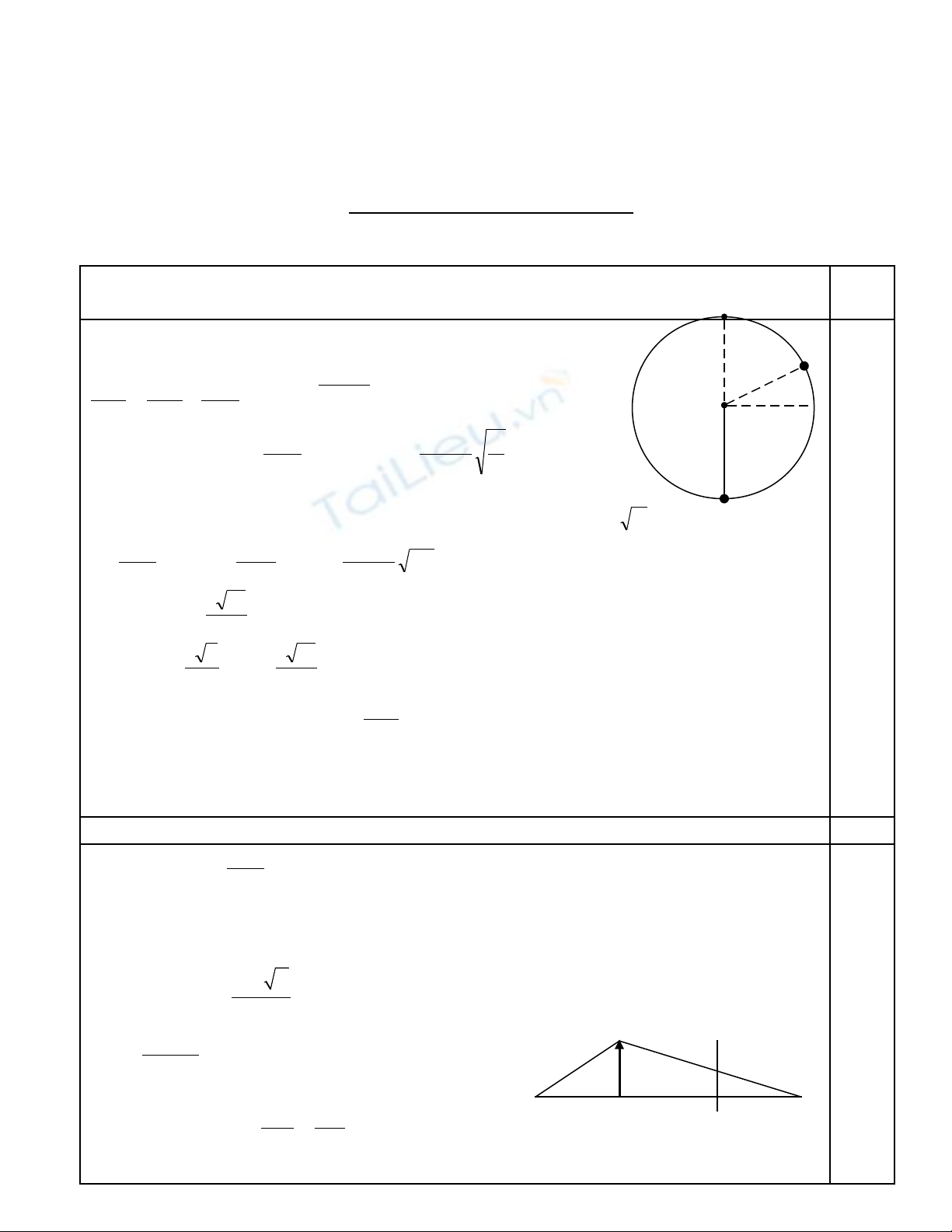
c/ C đnh t n s rung, thay đi kho ng cách Số ị ầ ố ổ ả 1S2. Đ l i quan sát đc hi n t ng giao thoaể ạ ượ ệ ượ
n đnh trên m t n c, ph i tăng kho ng cách Sổ ị ặ ướ ả ả 1S2 m t đo n ít nh t b ng bao nhiêu ? V iộ ạ ấ ằ ớ
kho ng cách y thì gi a Sả ấ ữ 1, S2 có bao nhiêu đi m có biên đ c c đi. Coi r ng khi có giao thoaể ộ ự ạ ằ
n đnh thì hai đi m Sổ ị ể 1S2 là hai đi m có biên đ c c ti u.ể ộ ự ể
=== H t ===ế
Thí sinh không đc s d ng b t c tài li u nàoượ ử ụ ấ ứ ệ
H NG D N CH M THI HSG V T LÍ 12 - Năm h c 2010 -2011ƯỚ Ẫ Ấ Ậ ọ
(g m 02 trang)ồ
Bài 1 (2,5đ)Điể
m
a/ Va ch m đàn h i:ạ ồ
2
Mv
2
mv
2
mv
Mvmvmv
2
2
2
1
2
0
210
=>
02 v
Mm
m2
v
Khi dây n m ngang: ằ
2
gl
m
Mm
vMgl
2
Mv
0
2
2
Thay s : vố0 = 3m/s.
b/ Đ M chuy n đng h t vòng tròn, t i đi m cao nh t E: ể ể ộ ế ạ ể ấ
glvE
=>
gl5
m2
Mm
v
2
Mv
l2Mg
2
Mv
0
E
2
2
.
Thay s : vố0 =
2
103
m/s.
c/ Khi
2
73
v0
m/s <
2
103
=> M không lên t i đi m cao nh t c a quĩ đo tròn.ớ ể ấ ủ ạ
L c căng c a dây: ự ủ
l
mv
cosmgT 2
. Khi T = 0 => M b t đu r i quĩ đo tròn t i D ắ ầ ờ ạ ạ
v i v n t c vớ ậ ố D, có h ng h p v i ph ng ngang góc 60ướ ợ ớ ươ 0.
T D v t M chuy n đng nh v t ném xiên. D dàng tính đc góc COD = 30ừ ậ ể ộ ư ậ ễ ượ 0.
* N u HS tính k h n ý c/ có th th ng đi m.ế ỹ ơ ể ưở ể
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
Bài 2 (2,5đ)
a/
0LfLdd
fd
df
d'ddL 2
;
Lf4L2
Đ có hai v trí c a th u kính đu cho nh rõ nét trên c a AB trên màn. thì pt ph i có 2 ể ị ủ ấ ề ả ủ ả
nghi m => Δ > 0 => L > 4f.ệ
b/ Nghi m ệ
1,2 2 1
L
d d d a
2
∆
= − =�
2 2
L a
f4L
−
=�
Thay s f = 20cm.ố
c/
O'S
N'S
IO
MN
IO'SMN'S
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
SS'
O
I
M
N
D
OC
E
f
L
d
L
f
d
'd
L'dd
IO
MN
Theo Côsi MNmin khi
Lfd
= 30cm.
0,25
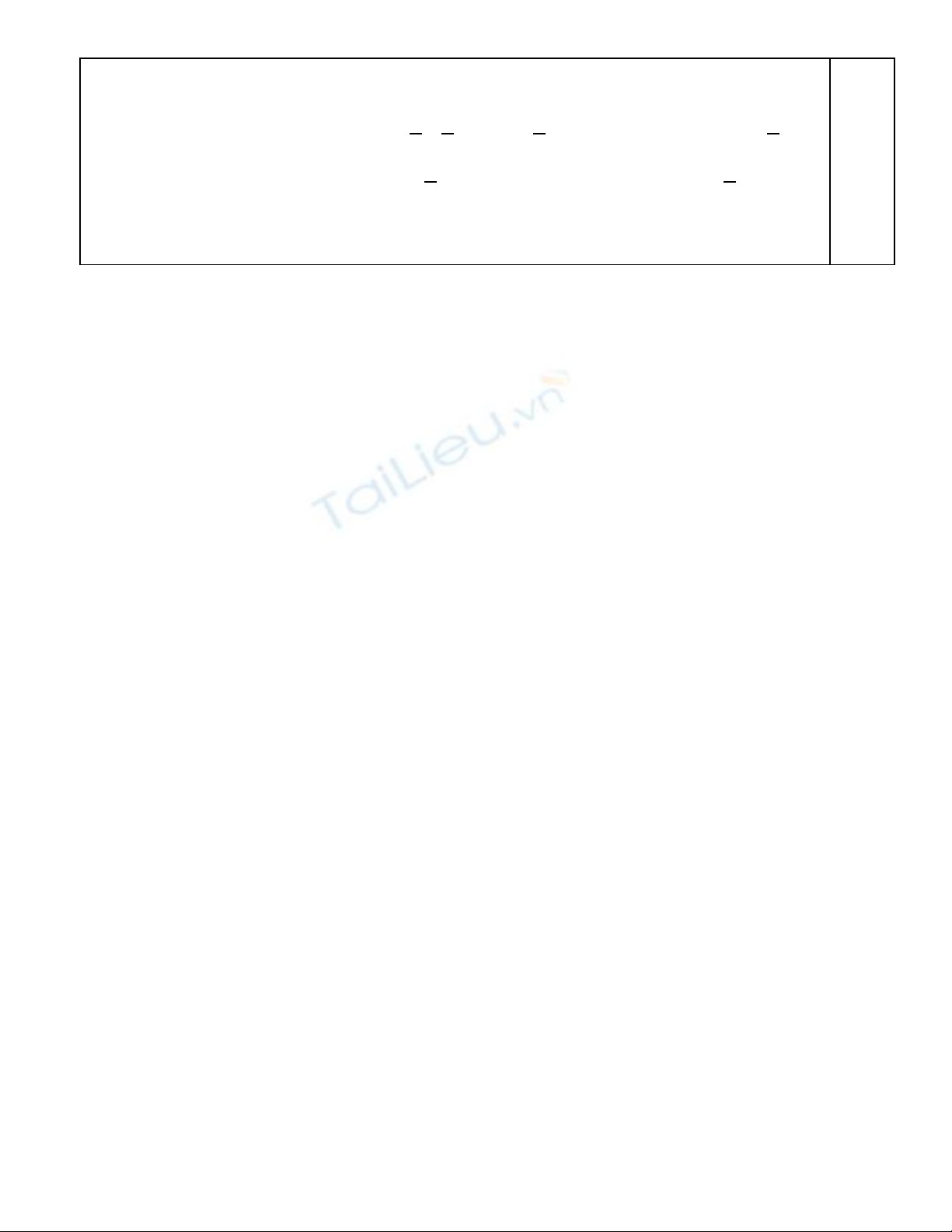
Bài 3 (2,5đ)
a/ T i VTCB ạ
l
sing
m
k
=> Δl = 1cm, ω =
510
rad/s, T =
s
55
.
Biên đ: A = ộ
2
0
2v
x
=> A = 2cm và
3
π
ϕ = −
.
V y: x = 2cos(ậ
10 5t 3
π
−
)cm.
b/ T i tạ1 v t M có v n t c vậ ở ậ ố 1, sau Δt =
54
= 1,25T.
- v t K (n u vậ ở ế 1 > 0) => t a đ xọ ộ 2 =
3
cm.
- v t N (n u vậ ở ế 1 < 0) => t a đ xọ ộ 2 = -
3
cm.
c/ Quãng đng m đi đc: - N u vườ ượ ế 1<0 => s1 =
11 3−
=> vtb = 26,4m/s.
- N u vế1>0 => s2 =
9 3+
=> vtb = 30,6m/s.
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
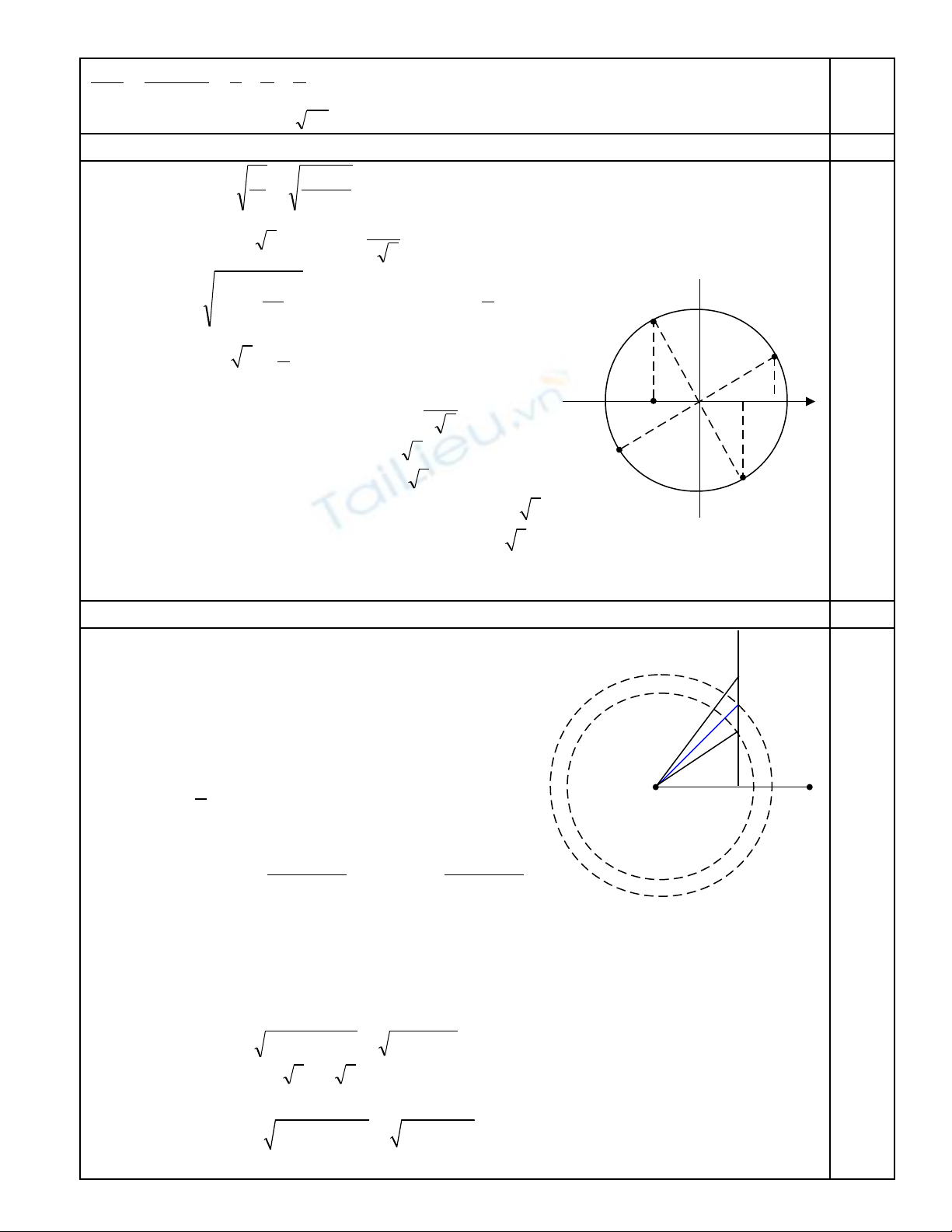
Bài 4 (2,5đ)
a. + = λ
f
v
= 0,8cm và d1 = d2 = d = 8cm
+ Ta có phương trình dao đngộ sóng t ngổ h pợ t iạ M1
uM1 = 2A cos
)dd(
t200cos
)dd( 2112
v i dớ1 + d2 = 16cm = 20λ và d2 – d1 = 0,
ta đc: uượ M1 = 2Acos(200πt - 20π)
b. Hai đi m Mể2 và M2’ g n Mầ1 ta có:
S1M2 = d + λ = 8 + 0,8 = 8,8 cm
S1M2’ = d – λ = 8 – 0,8 = 7,2 cm
Do đó: IM2 =
)cm(84,748,8ISMS 222
1
2
21
IM1 = S1I
)cm(93,6343
Suy ra M1M2 = 7,84 – 6,93 = 0,91 (cm)
T ng t : IMươ ự 2’ =
'2 2 2 2
1 2 1
S M S I 7,2 4 5,99(cm)− = − =
M1M2’ = 6,93 – 5,99 = 0,94 (cm)
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
O
-1 x
M
N
K
K'
M1
M2'
M2
S1I
c. Khi h sóng đã n đnh thì hai đi m Sệ ổ ị ể 1, S2 là hai tiêu đi m c a các hypecbol và r t ể ủ ở ấ
g n chúng xem g n đúng là đng yên, còn trung đi m I c a Sầ ầ ứ ể ủ 1S2 luôn n m trên vân giaoằ
thoa c c đi. Do đó ta có: Sự ạ 1I = S2I = k
4
)1k2(
42
=> S1S2 = 2S1I = (2k + 1)
2
Ban đu ta đã có: Sầ1S2 = 8cm = 10 = 20λ
2
=> ch c n tăng Sỉ ầ 1S2 m t kho ngộ ả
2
= 0,4cm.
Khi đó trên S1S2 có 21 đi m có biên đ c c đi. ể ộ ự ạ
0,25
0,25


























