Sở GDĐT Thừa thiên Huế ĐỀ THI THỬ ĐẠI HỌC KHỐI B-D (Lần 1)
Trường THPT Hai Bà Trưng Năm học: 2013-2014
(Thời gian làm bài: 180 phút)
Câu 1: (2điểm) Cho hàm số y =
2 1
2
x
x
có đồ thị (H)
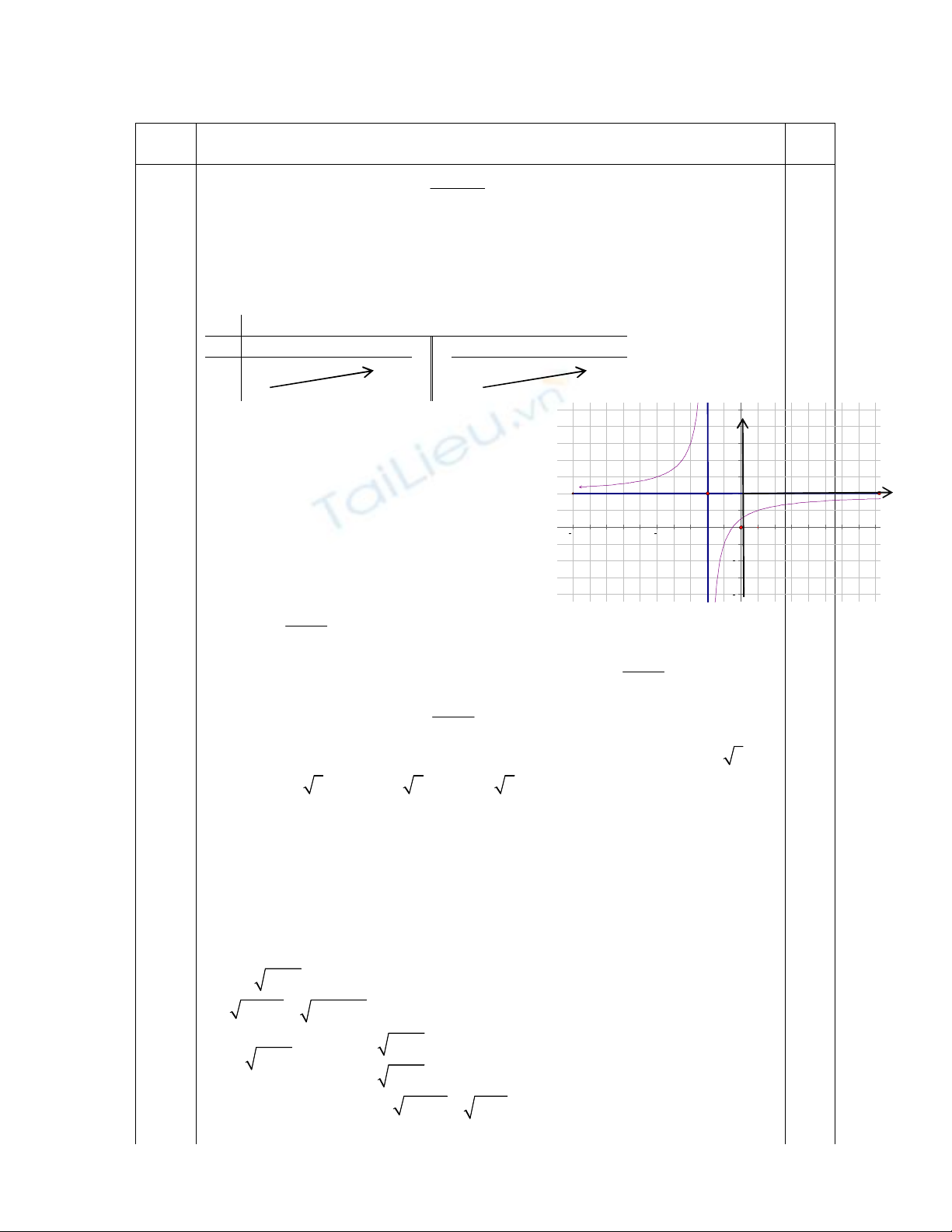
1/Khảo sát sự biến thiên và vẽ đồ thị (H).
2/Tìm bán kính đường tròn tâm I tiếp xúc (H). Với I là giao điểm hai tiệm cận của (H).
Câu 2: (3điểm) Giải các phương trình và hệ phương trình sau:
1/ 3 2 3
4(cos cos 3sin )
x x x
+ 2 2
x x x
=0
2/
9 2 .3 26 15.3 4
x x x
x x
3/ 3
2
23 1 1
x x y y
x y
Câu 3: (1điểm) Cho tập hợp A= {0; 2; 3; 6; 7}. Có mấy số tự nhiên gồm 4 chữ số khác nhau và
chia hết cho 6 được lấy từ tập hợp A.
Câu 4: (1điểm) Cho 3 số thực x, y, z đều lớn hơn 1 và x.y.z=64.
Tìm giá trị nhỏ nhất của biểu thức P=
log 3.log 9.log 27
x y z
Câu 5: (1điểm) Trong mặt phẳng tọa độ Oxy cho (d1): 2x+y-2=0; (d2): x-y-2=0;
(d3): x+y+2=0. Tìm các diểm A và C thuộc (d1); điểm B thuộc (d2); điểm D thuộc (d3) sao cho
ABCD là hình vuông.
Câu 6: (2điểm) Cho tứ diện ABCD; có AB = AC = AD; BC = a;
0 0
60 ; 90
BAD DAC BDC
1/Tính thể tích tứ diện ABCD; diện tích mặt cầu ngoại tiếp tứ diện đó theo a.
2/Tính khoảng cách giữa AD và BC.
---Hết---
Họ và tên thí sinh………………………………………………….Số báo danh…………………..
(Giám thị không giải thích gì thêm)
ĐÁP ÁN ĐỀ THI THỬ ĐẠI HỌC LẦN I KHỐI B, D 2013-2014
Câu Nội dung (Tóm tắt lời giải ) Điể
m
Câu
I/1
1
điểm
*Tập xác định D=R\
2
;y/ = 2
3
0
( 2)
x
x D
/s
h
đ/biến
; 2 2;
*
lim lim 2
x x
y y
 
; 2 2
lim ; lim
x x
y y
 
Đồ thị có t/cận đứng x=-2 và
t/cận ngang y=2
* Bảng biến thiên:
x - -2 +
y'
+
+
y
+
2
2
-
k/luận :
* Đồ thị (H) qua (0;1/2) ; (1;1); (-1/2;0) ; (-1;-1)
(H) nhận I(-2;2)làm tâm đối xứng
0.25
0.25
0.25
0.25
Câu
I/2
1
điểm
* Gọi M(a;
2 1
2
a
a
)
( )
H
; (C) là đường tròn tâm I(-2;2) tiếp xúc (H) ;P/trinh tiếp
tuyến với (H) tại M là đương thẳng (d):3x - (a+2)2y - 3a +
2 1
2
a
a
= 0 ; (a
-2)
* 2
3
(( 2) ;3); ( 2;
2)
d
u a IM a a
)
* (d) là tiếp tuyến của (C) tại M
4
. 0 ( 2) 9
d
IM u a
2 3
a
* Với a=-2
3
ta có IM=
6
.Vậy R=
6
0.25
0.25
0.25
0.25
Câu II
/1
1
điểm
* 3
2x
+2x.3
x
-13.3
x
-2.3
x
-4x+26=0
(3
x
-2).(3
x
+2x-13)=0
* 3 2 0
3 2 13 0
x
xx
; 3x-2=0
x=
3
log 2
* f(x)=3xlà hàm số đồng biến trên R ; g(x) =-2x+13 là hàm số nghịch biến trên R
; x=2 là một nghiệm của p/ trình : 3x=-2x+13=0
* Vậy p/trình đã cho có tập nghiệm S=
3
log 2;2
0.25
0.25
0.25
0.25
Câu II
/2
1
điểm
* 3
2
23 1 1
x x y y
x y
đ/k : 0
1
1 0
x y x y
y
x-y+ 1
2 0 1
2
x y
x y x y
x y
* Thay x=y+1 vào p/trình: 3
23 1 1
x y
ta có:
0.25
0.25
6
4
2
2
4
10 5 5
3
23 1 2 3 22 0
x x x x x x
* Đặt t=
x
đ/k: t
0 có : t3 + 2t2 + 3t – 22 = 0
t = 2
* Giải hệ có nghiệm: (4 ; 3)
0.25
0.25
Câu
III
1
ểm
*A = {0; 2; 3; 6; 7} có 5 tập con gồm 4 p/ tử đó là : A1 = {0;2 ; 3; 6}; A2 = {0;
2; 3; 7};
A3 = {0; 2; 6; 7} ; A4 = {2; 3; 6; 7} ; A5 = {0; 3; 6; 7}
Số tự nhiên gồm 4 chữ số chia hết cho 6 là vừa chia hết 3 vừa chia hết 2 chỉ lấy
trong tập:
A2; A3; A4.
*Tâp A2 có 2 dạng:
0
abc
và
2
abc
; dạng ;
0
abc
có: 3.2.1=6 số cần tìm; dạng
2
abc
có: 2.2.1=4 số cần tìm
*T/ tự tập A3 có 14 số cần tìm .Tập A4 có 2 dạng :
2
abc
;
6
abc
do đó có 12
số cần tìm
*Vậy có : 10+ 14 + 14 = 36 số cần tìm
0.25
0.25
0.25
0.25
Câu
IV
1
điểm
*Ta có : P = 222
2 2 2
log 3.log 9.log 27
log .log .log
x y z
= 3
2
2 2
6.log 3
log .log .log
z
x y
Mà :
3 3
2 2 2 2 2 . 2 2 .
log log log 3 log .log .log 6 3 log .log .log
x y z x y z x y z
2 2 2
8 log .log .log
x y z
3 3 3
2 2 2
2 2 2
6.log 3 6.log 3 3.log 3
log .log .log 8 4x y z
MinP = 3
2
3.log 3
4
khi : x = y = z = 4
0.25
0.25
0.25
0.25
Câu
V
1
điểm
*AC có véc tơ chỉ phương :
u
=(1;-2) ; A
(d1)C A(a ;-2a +2) ; B
(d2)
B(t ;
t-2) ;
D
(d3)
D(k ;-k-2) ;
BD
=(k-t ; -k-t) ;
BD
.
u
= 0
t + 3k = 0 (1)
*I là trung điểm của AB thì I
(d1) và I(
4
;
2 2
k t k t
)
k + 3t = 8 (2)
* Giải (1) và (2) ta có : B(3 ; 1) ; D(-1 ; -1)
* A
(d1) và C
(d1) ;
AB

=(a - 3 ; -2a + 1) ;
AD

=(a + 1; -2a + 3) ;
AB

.
AD
= 0
Giải ra có A(0 ; 2) và C(2 ; -2) hoặc C(0 ; 2) và A(2 ; -2)
0.25
0.25
0.25
0.25
Câu
VI
2
điểm
1/*hình vẽ 0.25 điểm .( H là trung điểm của BC ; I nằm ngoài đoạn AH)
* AH =
2 2
AB HB
=
2
a
đvdd
* V = 3
3
12
a đvtt
* E là trung điểm của AB ; trung trực đoạn AB trong mp(ABH) cắt AH tại I( I
nằm ngoài đoạn AH) ; khi đó : I là tâm mặt cầu ngoại tiếp tứ diện ABCD ;
AEI AHB
IA = a đvđd
* dt m/ cầu ngoại tiếp ABCD = 4
a2 đvdt
2/* Qua D kẻ đ/ thẳng (d)// BC ; kẻ HE
BC ; kẻ HK
AE khi đó k/c từ H đến
mp (ADE) =k/c giữa BC và AD
0.25
0.25
0.25
0.25
0.25
0.25
*Ta có DH1
BC tại H1 khi đó có DH1 = EH mà DH1.BC = DB.DC
DH1 =
EH =
6
3
a
*
2 2 2
1 1 1
HK HE HA
HK =
12
11
a đvdd
0.25
0.25