TRƯỜNG THPT QUỲNH LƯU 2 ĐỀ THI THỬ ĐẠI HỌC LẦN I NĂM HỌC 2011 -2012
TỔ TOÁN MÔN TOÁN KHỐI A , B
( Thời gian : 180 phút )
I ) PHẦN CHUNG CHO TẤT CẢ THÍ SINH ( 7 điểm )
Câu 1: (2 điểm)
Cho hàm số: 23 3xxy (C)
1) Khảo sát sự biến thiên và vẽ đồ thị hàm số (C)
2) Biện luận theo m0 số nghiệm của phương trình:
m
mxx 1
3
2
Câu 2 : ( 2 điểm )
1) Giải phương trình : 2 2
2sin 2sin t anx
4
x x
2) Giải hệ phương trình :
2 2
8
7
1
x y x y
x y
y x xy
Câu 3 : ( 1 điểm ) Tính tích phân : I =
42
0
sin 2 os2xdx
x x c
Câu 4 : ( 1 điểm )
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh bằng 3cm , các cạnh SA = SB =SC = 3cm
Tam giác SBD có diện tích bằng 6 cm2 .Tính thể tích của khối chóp SABCD .
Câu 5 : ( 1 điểm )Cho a, b,c là các số thực dương ,abc= 1. Tìm giá trị nhỏ nhất của biểu thức :
2 2 2 2 2 2
bc ca ab
A
II ) PHẦN RIÊNG CHO TỪNG BAN : ( 3 điểm )
( Thí sinh chỉ được làm một trong hai phần )
A ) Dành cho ban cơ bản :
Câu 6a :( 1 điểm )Trong không gian với hệ trục Oxyz viết phương trình mặt cầu ( S ) có tâm thuộc
trục Oz , cách mặt phẳng ( P ) có phương trình : 2x - y - 2z - 2 = 0 một khoảng bằng 2 và
cắt mp (P) theo đường tròn có bán kính bằng 3 .
Câu 7a : ( 1 điểm ) Giải bất phương trình :
2 2
1 5 2 1
2 5
log log 1 log log 1
x x x x
Câu 8a :(1 điểm ).Trong hệ toạ độ Oxy. Viết phương trình đường tròn đi qua điểm A(1; 2) có bán kính
bằng 1 đồng thời tiếp xúc với đường thẳng d có phương trình : 3x -4y -1 = 0.
B ) Dành cho ban nâng cao :
Câu 6b:( 1 điểm )Trong không gian với hệ trục Oxyz cho điểm A ( 2; 0; 0 ) H (1; ;1; 1) viết phương
trình mặt phẳng (P )đi qua điêm A, H sao cho mp (P ) cắt trục Oy , Oz lần lượt tại B ,C thỏa
mãn diện tích tam giác ABC bằng
4 6
Câu 7b : ( 1 điểm ) Giải bất phương trình : 1 1 1
3 3 4 0
x x
Câu 8b :(1 điểm ) Trong hệ toạ độ Oxy cho tam giác ABC có diện tích bằng
12 6 6
, t
ọa độ các
đỉnh A(-2; 0), B(4; 0) và độ dài bán kính đường tròn ngoại tiếp tam giác đó bằng 5. Tìm tọa độ điểm C
biết tung độ của nó là số dương.
........................................................................HẾT ....................................................................
2
ĐÁP ÁN – THANG ĐIỂM
Môn thi : TOÁN , khối A,B
Câu Nội dung Điểm
1 a) Với m = -1 hàm số trở thành : y = x3 -3 x2
Tập xác định : R
Sự biến thiên : y’ = 3 x2 – 6 x , y’ = 0
0
2
x
x
lim ; lim
x x
y
 
 
Bảng biên thiên :
x

0 2
y’ + 0 - 0 +
y
0

-4
hàm số đạt giá trị cực đại tại x =0 y cđ = 0 , cực tiểu tại x = 2 , y ct = -4
hàm số đồng biến trên các khoảng (

; 0 ) và ( 2 ;
)
hàm số nghịnh biến trên các khoảng ( 0; 2 )
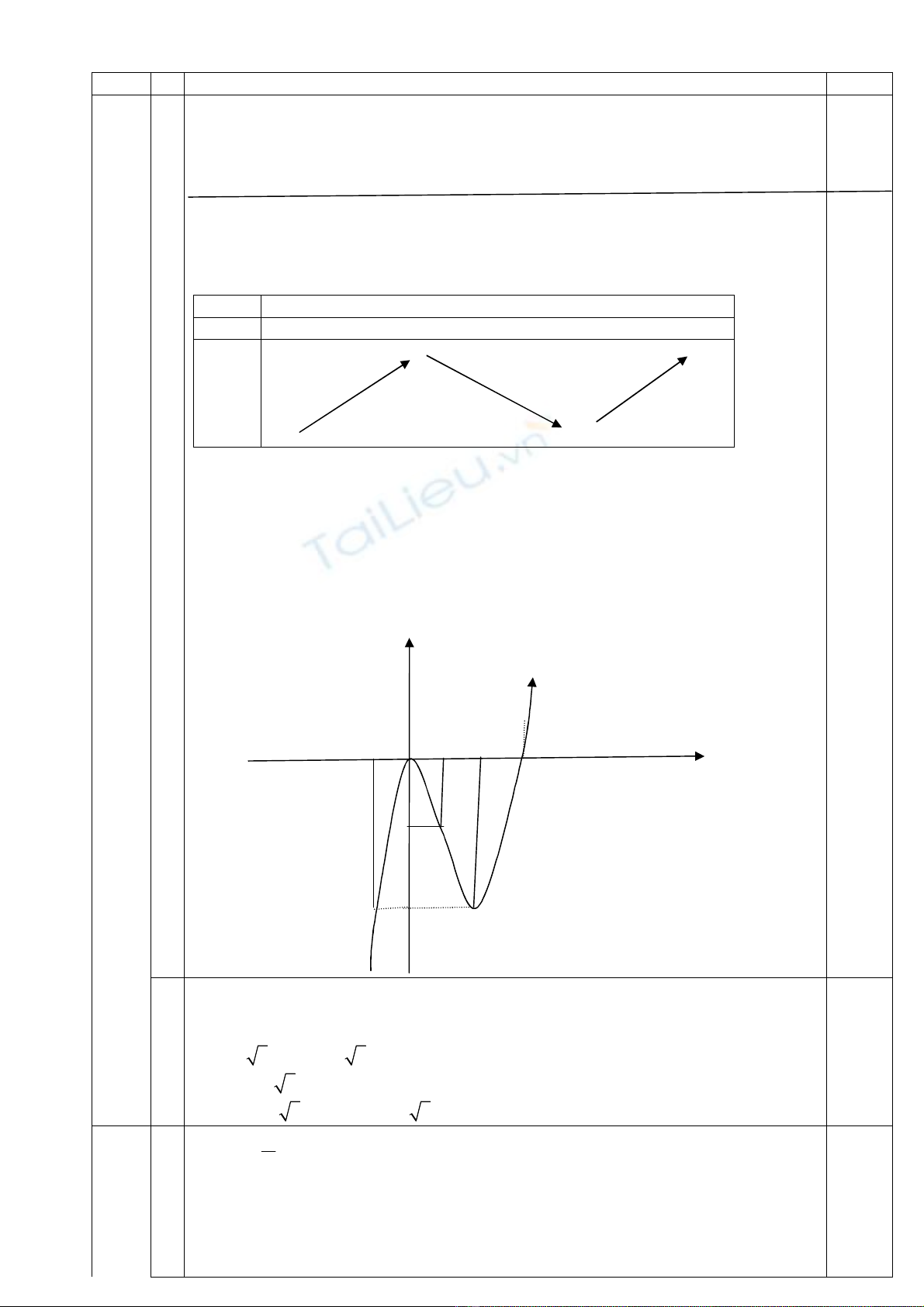
Đồ thị
Giao điểm đồ thị với trục tung tại điểm ( 0; 0 )
Giao điểm đồ thị với trục hoành tại điểm
Điểm uốn I ( 1 ; -1 )
0,25
0,25
0,25
0,25
b)
Giữ nguyên đồ thị (C ) với x lớn hơn hoặc bằng 3 . Lấy đối xứng qua trục hoành
phần đồ thị ứng với x < 3 .Ta có :
* ) m < 0 pt vô nhiệm
* )
2 3 2 3
m pt có 4 nghiệm phân biệt
*)
2 3
m pt có 3 nghiệm
* )
2 3 à 0 < m < 2 - 3
m v pt có 2 nghiệm
0,5
0.25
0,25
2 a) Đk :
2
x k
.
pt
cosx +sin2x .cosx – sin 2x sinx + sinx =0
( sinx + cosx ) ( 1- sin2x ) =0
0,25
0,25
0,5
1
3
2
1
-4
-
2
-1
y
x
3
sinx +cosx =0
sin2x =0
4 2
k
x
b)
Hệ
2
2
3
( ) 2 8
2
7
1
x y
x y x y xy x y
x y xy
x y xy
:
Vậy nghiệm của hệ là : (x;y) = (1 ;2) ,( 2 ; 1) ,( 1;-3 ) (-3; 1)
0,25
0,25
0,25
0,25
3
4 4 4 4
2 2
0 0 0 0
4
3
0
1 1
. os2xdx sin 2 cos2 sin 2 sin 2 (sin 2 )
2 2
1 1 1 1
( sin 2 os2x+ sin )
2 2 3 8 12
x c x xdx xd x xd x
x x c x
0,5
0,5
4
GọGọi H là hình chiếu của S trên (ABCD) suy ra H nằm trên BD (Vì SA = SB = = SC, BD
là trung trực của AC). Do đó SH đường cao của hình chóp cũng là đường cao của tam giác
SBD
; Gọi O là giao điểm của AC và BD. Vì SA = SC = DA = DC nên SO = DO suy ra tam
giác SBD là tam giác vuông tại S. Vì dt(SBD) = 6 và SB = 3 nên SD = 4; suy ra BD = 5,
SH = 12/5.
ABCD là hình thoi có AD = 3, DO = 5/2 nên AO =
11
2
suy ra dt(ABCD) =
5 11
2
.1
. ( ) 2 11
3
S ABCD
V SH dt ABCD . Vậy thể tích khối chóp S.ABCD bằng
2 11
.
Đặt x =bc , y= ca , z = ab ( x> 0 , y > 0 , z > 0 ) xyz = 1 . Ta có
2 2 2 2 2 2 2 2 2
b c c a b a x y z
A
ab ac bc ba ac bc y z x z x z
Áp dụng Cô si : 2
4
x y z
x
y z
Tư đó 3
3 3
2 2 2
x y z
A xyz
Dâu bằng xay ra khi x= y = z =1
0,25
0,25
0,25
0,25
6a Gọi tâm mặt cầu là I ( 0; 0 ; 2 ) thuộc trục Oz . Do k/c từ I đến mp P bằng 2 nên ta
có :
2
2 2 2
4
3
c
c
c
. Vậy I (0; 0; 2 ) và I ( 0 ;0 ; -4 ) Do (S ) cắt P theo
đương tròn có bán kính bằng 3 nên bán kính mặt câu ( S) là :
9 4 13
R
Vậy pt mặt cầu là :
2
2 2
2 13
x y z
và
2
2 2
4 13
x y z
0,25
0,25
0,25
0,25
7a Đk x> 0 Bpt
2 2
3 1 3 5
5
2 2
3 1 5
5
2 2 2 2
5 5
22
2
log log 1 log log 1 0
log log 1 log 1 0
log 1 1 0 log 1 1 1 5
5 0 12
1 5 5
1 5
x x x x
x x x x
x x x x x x
x
x x x
x x
Kết hợp đk ta có 0 < x <
12
5
0,25
0,5
0,25
4
8a Gọi tâm đương tròn (C ) là I (a; b) .Do (C ) có bán kính bằng 1 , tiếp xúc với d và
điểm A thuộc ( C ) nên ta có hệ pt :
2 2
2 2
2 2 2
2 2 2
1 2 1
1 2 1 3 4 6
3 4 1 5 3 4 4
3 4 6 3 4 6
ê ô nghiêm
4 3 3 6 9 25 12 36 0
3 4 4 3 4 4
46 256
25
25 92 76 0
4 7 3 6 9
a b
a b a b
a b a b
a b a b h v
b b b b a
a b a b b
b b
b b
Vậy pt đường tròn là :
0,25
0,25
0,25
0,25
6b mpP c
ắt trục 0y tại B (0; b ;0 ) cắt truc Oz tại điểm C (0; 0 ; c )
Pt mp P có dạng :
1
2
x y z
b c
điểm H thuộc mpP nên :
1 1 1 1 2
2
b c bc
b c
(1)
2 2 2 2 2 2 2 2
1
; 4( ) 8 6 4( ) 64.6 2
2
ABC
S AB AC b c b c b c b c
Từ(1) và (2) ta có :
4
8
3 21
83 21
16 2
62&
6
3 21
23 21
12 2
2
b c
b c
b c b
bc b
b c b c
bc b c c
bc c
0,25
0,25
0,25
0,25
7b Đk :
1
x
Pt 1
2 1 1
1
3 3 1 1 0
3 4.3 3 0
1
1 0
3 1
x
x x
x
x x
x
x
Nghiệm bất pt là : T =
1 0;

0,25
0,5
0,25
8b Giọi I(x0; y0) là tâm đường tròn ngoại tiếp ABC, suy ra PT đường tròn (C) ngoại
tiếp tam giác ABC là:
(x – x0)2 + (y – y0)2 = 25. Vì điểm A(-2; 0), B(4; 0) thuộc đường tròn nên đường
tròn ( C) có PT là:
(x – 1)2 + (y – 4)2 = 25 , (x – 1)2 + (y + 4)2 = 25.
(Tìm tâm của đường tròn ngoại tiếp tam giác ABC, có thể vẽ hình rồi sử dụng tam giác vuông,
lưu ý hai trường hợp)
Vì A(-2; 0), B(4; 0) và dt(ABC) =
12 6 6
nên đường cao CH =
4 2 6
. Hai
điểm A, B nằm trên trục hoành và C có tung độ là số dương nên C năm trên đường
thẳng y =
4 2 6
Do đó tọa độ điểm C là nghiệm của hệ
2 2
x – 1 y – 4 25
4 2 6y
(1) và
2 2
x – 1 y + 4 25
4 2 6y
(2)
Giải hệ (1), (2) ta có điểm C(0;
4 2 6
), C(2;
4 2 6
).
0,25
0,25
0,25
0,25
Thí sinh có thể làm cách khác mà kết quả đúng vẫn đạt điểm tối đa .
5