Đ THI TH Đ I H C, CAO Đ NG NĂM 2010Ề Ử Ạ Ọ Ẳ
Môn thi : TOÁN (Đ 126 )Ề
I. PH N CHUNG CHO T T C THÍ SINH (7 đi m).Ầ Ấ Ả ể
Câu I (2 đi m): ểCho hµm sè
2 1
1
x
yx
+
=+
1. Kh¶o s¸t sù biÕn thiªn vµ vÏ ®å thÞ (C) cña hµm sè ®· cho.
2. T×m trªn (C) nh÷ng ®iÓm cã tæng kho¶ng c¸ch ®Õn hai tiÖm cËn cña (C) nhá nhÊt
Câu II (2 đi m):ể1) Gi i ph ng trình: ả ươ
2 2
2009
cos 2 2 2 sin 4cos sin 4sin cos
4
x x x x x x
π
� �
+ + = +
� �
� �
.
2) Gi i h ph ng trình: ả ệ ươ
2
2
3
2 3
1 1
(1 ) 4
14
x x y y
x x x
y y y
+ + + =
+ + = −
.
Câu III (1 đi m):ể Tính tích phân:
02
2
1
2
3 4 4 . 2 1
4 4 5
x x
I x x dx
x x
−
� �
− −
= + +
� �
� �
+ +
� �
.
Câu IV (1 đi m):ểTrên đ ng th ng vuông góc t i ườ ẳ ạ A v i m t ph ng c a hình vuông ớ ặ ẳ ủ ABCD c nh ạa ta
l y đi m ấ ể S v i ớSA = 2a . G i ọB’, D’ là hình chi u vuông góc c a ế ủ A lên SB và SD. M t ph ng (ặ ẳ AB’D’ )
c t ắSC t i ạC’ . Tính th tích kh i đa di n ể ố ệ ABCDD’ C’ B’.
Câu V (1 đi m):ể Tam gi¸c ABC cã ®Æc ®iÓm g× nÕu c¸c gãc tho¶ m·n:
cos .cos cos .cos cos .cos 3 ?
cos cos cos 2
A B B C C A
C A B
+ + =
II. PH N RIÊNG CHO T NG CH NG TRÌNH ( 3 đi m).Ầ Ừ ƯƠ ể
Thí sinh ch đ c làm m t trong hai ph n (ph n 1 ho c ph n 2)ỉ ượ ộ ầ ầ ặ ầ
1. Theo ch ng trình Chu n:ươ ẩ
1. Câu VI.a (2 đi m): ể 1) Trong m t ph ng to đ Oxy , cho đ ng tròn ( C) :ặ ẳ ạ ộ ườ
2 2 2 6 15 0x y x y+ − + − =
và đ ng th ng (d) : ườ ẳ
3 0mx y m− − =
( m là tham s ). G i I là tâmố ọ
c a đ ng tròn . Tìm ủ ườ m đ đ ng th ng (d) c t (C) t i 2 đi m phân bi t A,B tho mãn chu viể ườ ẳ ắ ạ ể ệ ả
∆
IAB b ng ằ
.
2) Trong không gian v i h t a đ ớ ệ ọ ộ Oxyz cho hai đ ng th ngườ ẳ :
1
1 1
( ) : 2 1 1
x y z
d− +
= =
−
và
2
2 1
( ) : 1 1 1
x y z
d− +
= =
−
. Vi t ph ng trình m t ph ng ch a (ế ươ ặ ẳ ứ d1) và h p v i (ợ ớ d2) m t góc 30ộ0.
Câu VII.a (1 đi m):ể Ch ng minh r ng v i ứ ằ ớ a, b, c>0 ta có:
1 1 1 1 1 1 1 1 1
4 4 4 3 3 3 2 2 2a b c a b b c c a a b c b c a c a b
+ + + + + +
+ + + + + + + + +
2. Theo ch ng trình Nâng cao:ươ
Câu VI.b (2 đi m) ể1) Trong m t ph ng Oxy cho đ ng tròn (C) tâm ặ ẳ ườ I(-1; 1), bán kính R=1, M là m tộ
đi m trên ể
( ) : 2 0d x y− + =
. Hai ti p tuy n qua ế ế M t o v i (ạ ớ d) m t góc 45ộ0 ti p xúc v i (C) t i ế ớ ạ A, B.
Vi t ph ng trình đ ng th ng ế ươ ườ ẳ AB.
2) Trong không gian Oxyz cho t di n ứ ệ ABCD bi t ếA(0; 0; 2), B(-2; 2; 0), C(2; 0; 2),
( )DH ABC⊥
và
3DH
=
v i ớH là tr c tâm tam giác ựABC. Tính góc gi a (ữDAB) và (ABC).
Câu VII.b (1 đi m): ể Ch ng minh r ng v i ứ ằ ớ a, b, c>0 ta có:
1
( )( ) ( )( ) ( )( )
a b c
a a b a c b b a b c c c a c b
+ +
+ + + + + + + + +
.
ĐÁP ÁN THI TH L N 2 NĂM 2008- 2009- MÔN TOÁN.Ử Ầ
I. PH N CHUNG.Ầ
Câu Ph nầN i dungộĐi mể
Câu I
(2,0)
1(1,0) HS tù gi¶i
2(1,0) HS tù gi¶i
Câu Ph nầN i dungộĐi mể
Câu II
(2,0)
1(1,0)
2 2
2009
cos 2 2 2 sin 4cos sin 4sin cos
4
x x x x x x
π
� �
+ + = +
� �
� �
2 2
cos sin 2(sin cos ) 4sin .cos (sin cos )x x x x x x x x− + + = +�
(cos sin )(cos sin 4cos .sin 2) 0x x x x x x+ − − + =�
cos sin 0 (1)
cos sin 4sin .cos 2 0 (2)
x x
x x x x
+ =
− − + =
+ Gi i (1): ả
(1) tan 1 4
x x k
ππ
= − = − +� �
+ Gi i (2): Đ t ả ặ
cos sin , 2x x t t− =
ta có ph ng trình: ươ
2
2 0t t+ =
.
0
1/ 2
t
t
=
= −
•V i ớ
0t
=
ta có:
tan 1 4
x x k
ππ
= = +�
•V i ớ
1/ 2t= −
ta có:
arccos( 2 / 4) / 4 2
cos( ) 2 / 4
4arccos( 2 / 4) / 4 2
x k
xx k
π π
π
π π
= − − +
+ = − = − − − +
KL: V y ph ng trình có 4 h nghi m: ậ ươ ọ ệ
4
x k
ππ
= − +
,
4
x k
ππ
= +
,
arccos( 2 / 4) / 4 2x k
π π
= − − +
,
arccos( 2 / 4) / 4 2x k
π π
= − − − +
.
0,5
0,25
0,25
2(1,0)
§k
0y
22
2
23
3
3
2 3
1 1 1 1
(1 ) 4 4
1 1
1( ) 4
4
x x x x
y y y y
x
x x x x
xy y y
y y y
+ + + = + + + =
� �
� �
� � + + + =
+ + = −
� �
®Æt
1
a x y
x
by
= +
=
Ta ®îc
2 2 2
3 3 2 2
2 4 4 2 4 2 2
1
2 4 ( 4) 4 4 4 0
a a b a a b a a b a
b
a ab a a a a a a
� � �
+ − = + − = + − = =
� � �
� � �
� � � � =
− = − + − = − + =
� � �
� � �
Khi ®ã
1
11
2
x y y
x
xx
=
=
� � =
+ =
KL
0,25
0,25
0,25
0,25
Câu Ph nầN i dungộĐi mể
Câu III
(1,0)
02
2
1
2
3 4 4 . 2 1
(2 1) 4
x x
I x x dx
x
−
� �
− −
= + +
� �
� �
+ +
� �
0 0
2
2
1 1
2 2
4 (2 1) ( . 2 1)
(2 1) 4
xdx x x dx
x
− −
− +
= + +
+ +
� �
0,25
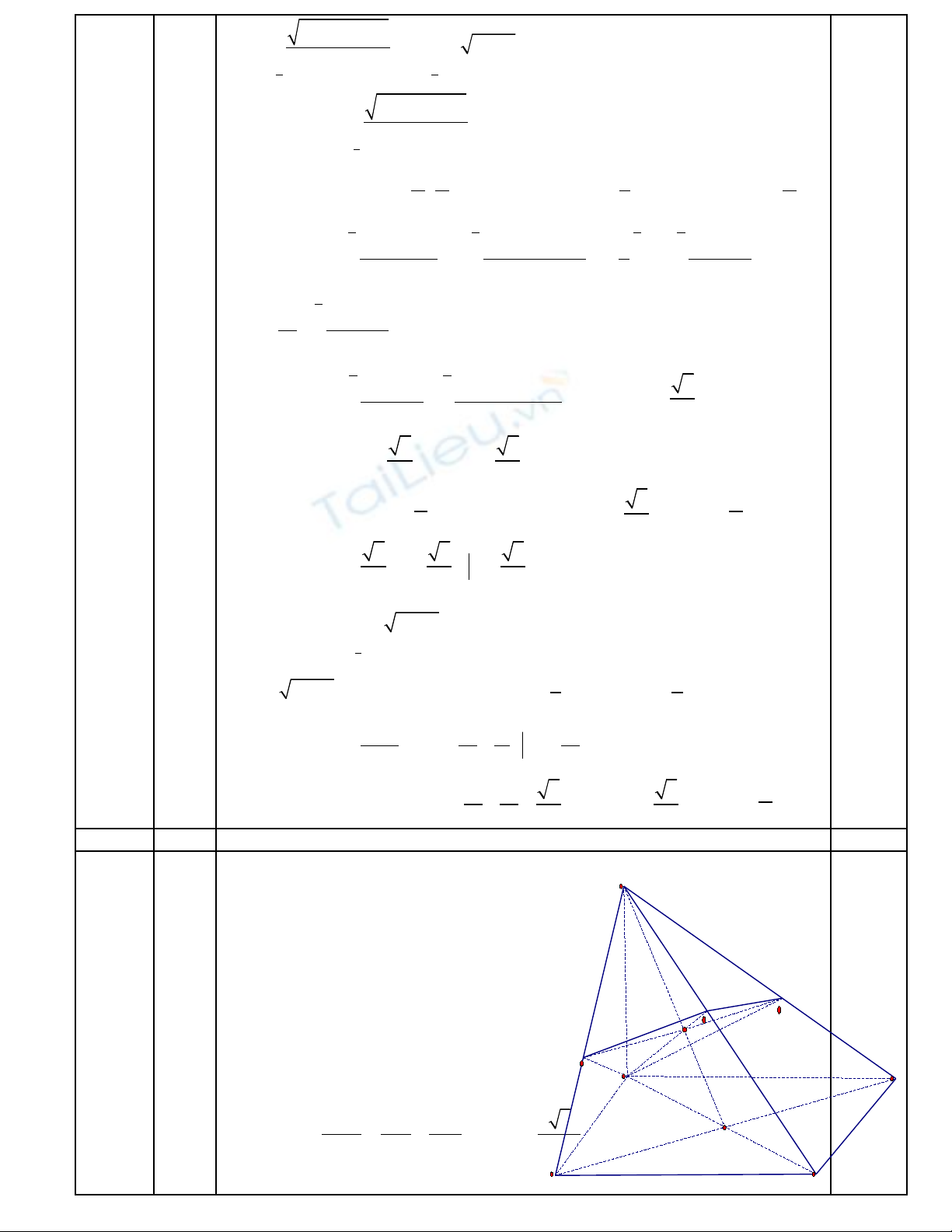
0 0
2
2
1 1
2 2
4 (2 1) ( . 2 1)
(2 1) 4
xdx x x dx
x
− −
− +
= + +
+ +
� �
+ Tính:
02
12
1
2
4 (2 1)
(2 1) 4
x
I dx
x
−
− +
=+ +
. Đ t:ặ
1
2 1 2sin , ; cos , 0, 0
2 2 2 6
x t t dx tdt x t x t
π π π
� �
+ = − = = − = = =� � � �
� �
� �
.
Khi đó:
2 2
6 6 6 6
12 2 2
0 0 0 0
2cos 2 1 sin 1
4sin 4 2(sin 1) 2 sin 1
t tdt dt
I dt dt
t t t
π π π π
− −
= = = − +
+ + +
� � � �
=
6
2
0
12 sin 1
dt
t
π
π
− + +
+ Tính:
6 6
22 2
0 0
(tan )
sin 1 2(tan 1/ 2)
dt d t
It t
π π
= =
+ +
� �
. Đ t: ặ
2
tan tan
2
t y=
.
Suy ra:
2
2 2
(tan ) (tan ) (1 tan )
2 2
d t d y y dy= = +
, v iớ
0 0, 6
t y t y
πϕ
= = = =� �
sao cho
6
tan 3
ϕ
=
,
(0 )
2
π
ϕ
< <
Khi đó:
2 0
0
2 2 2 .
2 2 2
I dy y
ϕϕ
ϕ
= = =
+ Tính:
0
3
1
2
( . 2 1)I x x dx
−
= +
. Đ t:ặ
2
1 1
2 1 2 1, , 0, 1
2 2
t x x t dx tdt x t x t= + = − = = − = = − =� � �
.
Khi đó:
12 5 3
2 1
2 0
0
1 1
2 10 6 15
t t t
I t dt � �
−
= = − = −
� �
� �
KL: V y ậ
1 2 3
1 2
15 12 2
I I I I
πϕ
= + + = − − +
, (
6
tan 3
ϕ
=
,
(0 )
2
π
ϕ
< <
)
0,25
0,25
0,25
Câu Ph nầN i dungộĐi mể
Câu IV
(1,0)
+ Trong tam giác SAB h ạ
'AB SC⊥
.
Trong tam giác SAD h ạ
'AD SD
⊥
.
D có: ễ
, ( )BC SA BC BA BC SAB⊥ ⊥ ⊥�
Suy ra:
'AB BC⊥
, mà
'AB SB⊥
. T đó có ừ
' ( ) ' (1)AB SAC AB SC⊥ ⊥�
.
T ng t ta có: ươ ự
' (2)AD SC⊥
. T (1) và (2)ừ
suy ra:
( ' ') ' 'SC AB D B D SC⊥ ⊥�
.
T đó suy ra: ừ
' ( ' ' ')SC AB C D⊥
+ Ta có:
2 2 2
1 1 1 2 5
'
' 5
a
AB
AB SA BA
= + =�
0,25
O
AD
BC
S
C'
B'
D'
2 2 2 2
4 4 5
' ' 4 5 5
SB SA AB a a a= − = − =�
,
2 2
5SB SA AB a= + =
.
Suy ra:
' 4
5
SB
SB =
;
L i có ạB’D’ // BD (cùng thu c mp(ộSBD) và cùng vuông góc v i ớSC) nên
' ' 'B D AC
⊥
(vì d cóễ
( )BD SAC⊥
nên
'BD AC
⊥
).
Xét hai tam giác đ ng d ng ồ ạ SB’D’ và SBD suy ra:
' ' ' 4
5
B D SB
BD SB
= =
4 2
' ' 5
a
B D =�
.
Ta có:
2 2
2 2 2
1 1 1 2 3 2 6
' ' '
' 3 3
a
AC SC SA AC a
AC SA AC
= + = = − =� �
+ Ta có:
3
. ' ' ' ' ' '
1 1 1 16
. ' . ' '. '. '
3 3 2 45
S AB C D AB C D
V S SC B D AC SC a= = =
.
3
.
1 2
.
3 3
S ABCD ABCD
V S SA a= =
. Suy ra th tích đa di n c n tìm là:ể ệ ầ
3
. . ' ' '
14
45
S ABCD S AB C D
V V V a= − =
.
Chú ý: V hình sai không ch m.ẽ ấ
0,5
0,25
Câu Ph nầN i dungộĐi mể
Câu
VIIa
(1,0)
D có: ễ
2
1 1 4
( ) 4 ( , 0)(*)x y xy x y
x y x y
+ + <�� � +
.
+ Ch ng minh: ứ
1 1 1 1 1 1
4 4 4 3 3 3a b c a b b c c a
+ + + +
+ + +
.
Áp d ng 2 l n (*) ta có: ụ ầ
1 1 1 1 16
3a b b b a b
+ + + +
hay
1 3 16
3a b a b
+ +
(1)
T ng t ta có: ươ ự
1 3 16
3b c b c
+ +
(2) và
1 3 16
3c a c a
+ +
(3)
C ng (1), (2) và (3) theo v v i v r i rút g n ta có đi u ph i ch ngộ ế ớ ế ồ ọ ề ả ứ
minh.
+ Ch ng minh: ứ
1 1 1 1 1 1
3 3 3 2 2 2a b b c c a a b c b c a c a b
+ + + +
+ + + + + + + + +
Áp d ng (*) ta có: ụ
1 1 4 2
3 2 2( 2 ) 2a b b c a a b c a b c
+ =
+ + + + + + +
(4)
T ng t ta có: ươ ự
1 1 2 (5)
3 2 2b c c a b b c a
+
+ + + + +
1 1 2 (6)
3 2 2c a a b c c a b
+
+ + + + +
C ng (4), (5) và (6) theo v v i v ta có đi u ph i ch ng minh.ộ ế ớ ế ề ả ứ
0,25
0,25
0,25
0,25
II. PH N RIÊNG.1. Ch ng trình Chu n.Ầ ươ ẩ
Câu Ph nầN i dungộĐi mể
CâuVIa.
(1,0)
1(1,0)
Câu Ph nầN i dungộĐi mể
CâuVIa. 2(1,0) Gi s m t ph ng c n tìm là: ả ử ặ ẳ ầ
2 2 2
( ) : 0 ( 0)ax by cz d a b c
α
+ + + = + + >
.
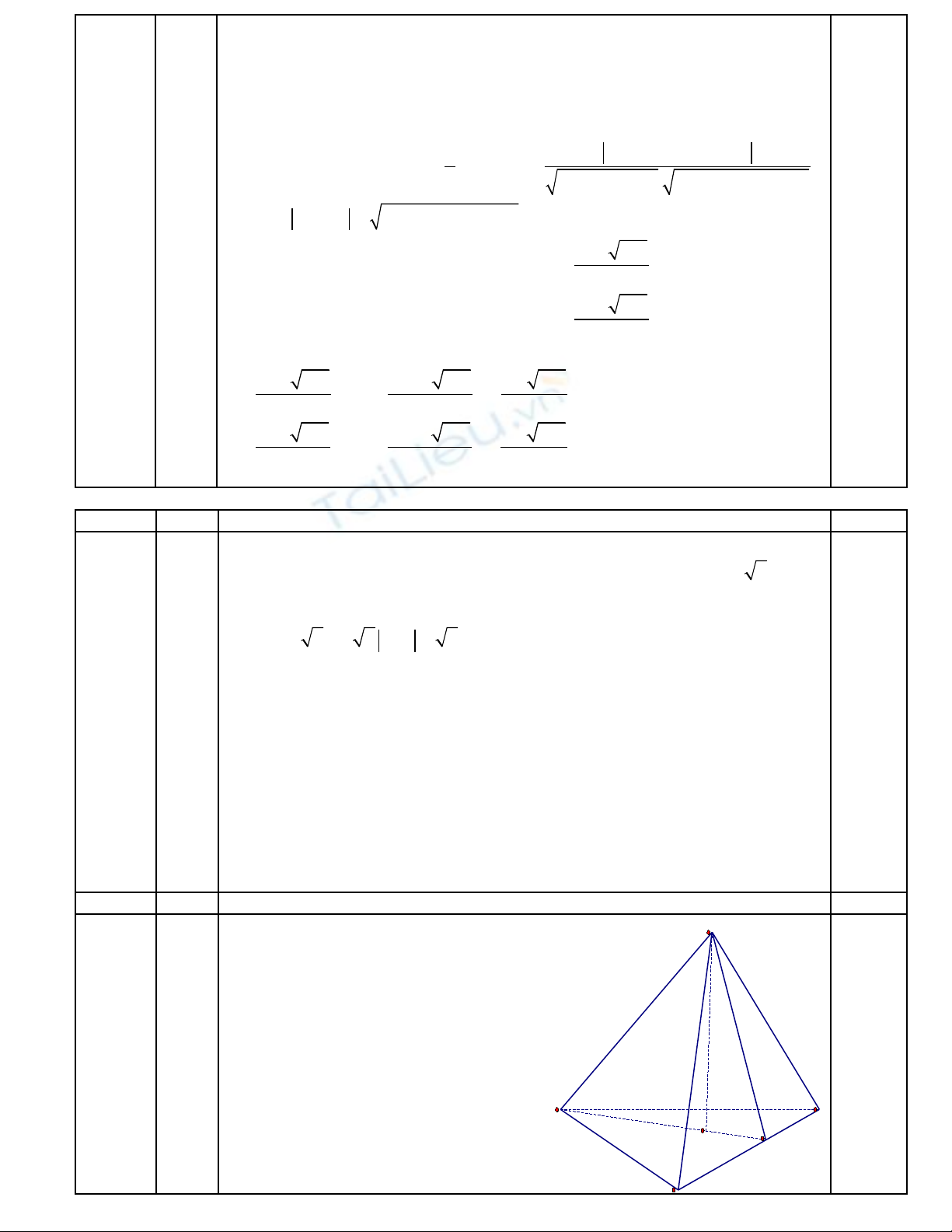
(1,0) Trên đ ng th ng (ườ ẳ d1) l y 2 đi m: ấ ể A(1; 0; -1), B(-1; 1; 0).
Do
( )
α
qua A, B nên:
0 2
0
a c d c a b
a b d d a b
− + = = −
� �
� �
− + + = = −
� �
nên
( ) : (2 ) 0ax by a b z a b
α
+ + − + − =
.
Yêu c u bài toán cho ta: ầ
0
2 2 2 2 2 2
1. 1. 1.(2 )
1sin 30
21 ( 1) 1 . (2 )
a b a b
a b a b
− + −
= = + − + + + −
2 2 2 2
2 3 2 3(5 4 2 ) 21 36 10 0a b a ab b a ab b− = − + − + =� �
D th y ễ ấ
0b
nên ch n ọb=1, suy ra:
18 114
21
18 114
21
a
a
−
=
+
=
KL: V y có 2 m t ph ng th a mãn:ậ ặ ẳ ỏ
18 114 15 2 114 3 114 0
21 21 21
x y z
+ + −
+ + − =
18 114 15 2 114 3 114 0
21 21 21
x y z
− − +
+ + − =
.
0,25
0,25
0,25
0,25
2. Ch ng trình Nâng cao.ươ
Câu Ph nầN i dungộĐi mể
CâuVIb
.
(1,0)
1(1,0) D th y ễ ấ
( )I d
. Hai ti p tuy n h p v i (ế ế ợ ớ d) m t góc 45ộ0 suy ra tam giác
MAB vuông cân và tam giác IAM cũng vuông cân . Suy ra:
2IM =
.
( ) (M d M� �
a; a+2),
( 1; 1)IM a a= + +
uuur
,
0
2 2 1 2 2
a
IM a a
=
= + =� � = −
.
Suy ra có 2 đi m th a mãn: ể ỏ M1(0; 2) và M2 (-2; 0).
+ Đ ng tròn tâm ườ M1 bán kinh R1=1 là (C1):
2 2
4 3 0x y y+ − + =
.
Khi đó AB đi qua giao đi m c a (C ) và (Cể ủ 1) nên AB:
2 2 2 2
4 3 2 2 1 1 0x y y x y x y x y+ − + = + + − + + − =�
.
+ Đ ng tròn tâm ườ M2 bán kinh R2=1 là (C2):
2 2
4 3 0x y x+ + + =
.
Khi đó AB đi qua giao đi m c a (C ) và (Cể ủ 2) nên AB:
2 2 2 2
4 3 2 2 1 1 0x y x x y x y x y+ + + = + + − + + + =�
.
+ KL: V y có hai đ ng th ng th a mãn: ậ ườ ẳ ỏ
1 0x y+ − =
và
1 0x y+ + =
.
0,5
0,25
0,25
Câu Ph nầN i dungộĐi mể
CâuVIb
.
(1,0)
2(1,0) Trong tam giác ABC, g i ọ
K CH AB=
.
Khi đó, d th y ễ ấ
( )AB DCK⊥
. Suy ra góc gi a (ữDAB) và
(ABC) chính là góc
DKH
.Ta tìm t a đ đi m ọ ộ ể H r iồ
Tính đ c ượ HK là xong.
+ Ph ng trình m t ph ng (ươ ặ ẳ ABC).
- Vecto pháp tuy n ế
( )
[ , ] 0; 4; 4n AB AC= = − −
r uuur uuur
- (ABC):
2 0y z+ − =
.
+
( )H ABC
nên gi s ả ử
( ; ;2 )H a b b−
.
Ta có:
( ; ; ), (4; 2;2).AH a b b BC= − = −
uuur uuur
( 2; ; ), ( 2;2; 2).CH a b b AB= − − = − −
uuur uuur
0,25
CA
B
D
HK