ðỀ THI THỬ TOÁN ðẠI HỌC - CAO ðẲNG
NGÀY 8 – THÁNG 6 - NĂM 2010
PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7 ñiểm)
Câu I (2 ñiểm)
Cho hµm sè
1
12
−
+
=
x
x
y
cã ®å thÞ (C).
1. Kh¶o s¸t sù biÕn thiªn vµ vÏ ®å thÞ hµm sè .
2. Víi ®iÓm M bÊt kú thuéc ®å thÞ (C) tiÕp tuyÕn t¹i M c¾t 2 tiÖm cËn t¹i Avµ B .
Gäi I lµ giao hai tiÖm cËn , T×m vÞ trÝ cña M ®Ó chu vi tam gi¸c IAB ®¹t gi¸ trÞ nhá nhÊt
Câu II (2 ñiểm) :
1. Giải hệ phương trình:
2 2
2 2
12
12
x y x y
y x y
+ + − =
− =
2.Giải phương trình:
( )
(
)
3
sin 2 cos 3 2 3 os 3 3 os2 8 3 cos sinx 3 3 0x x c x c x x+ − − + − − =
.
Câu III: Tính diện tích của miền phẳng giới hạn bởi các ñường
2
| 4 |y x x= −
và
2y x=
.
Câu IV (1 ñiểm) Cho hình chóp cụt tam giác ñều ngoại tiếp một hình cầu bán kính r cho trước. Tính thể tích hình
chóp cụt biết rằng cạnh ñáy lớn gấp ñôi cạnh ñáy nhỏ.
Câu V (1 ñiểm) Cho phương trình
( ) ( )
3
4
1 2 1 2 1
x x m x x x x m
+ − + − − − =
Tìm m ñể phương trình có một nghiệm duy nhất.
PHẦN RIÊNG (3 ñiểm): Thí sinh chỉ làm một trong hai phần (Phần 1 hoặc phần 2)
1. Theo chương trình chuẩn.
Câu VI.a (2 ñiểm)
1. Cho
∆
ABC có ñỉnh A(1;2), ñường trung tuyến BM:
2 1 0x y
+ + =
và phân giác trong CD:
1 0x y
+ − =
. Viết phương trình ñường thẳng BC.
2. Cho ñường thẳng (D) có phương trình:
2
2
2 2
x t
y t
z t
= − +
= −
= +
.Gọi
∆
là ñường thẳng qua ñiểm
A(4;0;-1) song song với (D) và I(-2;0;2) là hình chiếu vuông góc của A trên (D). Trong các mặt phẳng qua
∆
,
hãy viết phương trình của mặt phẳng có khoảng cách ñến (D) là lớn nhất.
Câu VII.a (1 ñiểm) Cho x, y, z là 3 số thực thuộc (0;1]. Chứng minh rằng
1 1 1 5
1 1 1
xy yz zx x y z
+ + ≤
+ + + + +
2. Theo chương trình nâng cao.
Câu VI.b (2 ñiểm)
1. Cho hình bình hành ABCD có diện tích bằng 4. Biết A(1;0), B(0;2) và giao ñiểm I của hai ñường chéo nằm
trên ñường thẳng y = x. Tìm tọa ñộ ñỉnh C và D.
2. Cho hai ñiểm A(1;5;0), B(3;3;6) và ñường thẳng
∆
có phương trình tham số
1 2
1
2
x t
y t
z t
= − +
= −
=
.Một ñiểm M thay
ñổi trên ñường thẳng
∆
, tìm ñiểm M ñể chu vi tam giác MAB ñạt giá trị nhỏ nhất.
Câu VII.b (1 ñiểm) Cho a, b, c là ba cạnh tam giác. Chứng minh
1 1 2 2
3 3 2 3 3
b c
aa b a c a b c a c a b
+ + + + <
+ + + + + +
----------------------Hết----------------------
http://laisac.page.tl
Kú thi thö ®¹i häc- cao ®¼ng n¨m 2010
H−íng dÉn chÊm m«n to¸n
C©u Néi dung §iÓm
I.1
Kh¶o s¸t hµm sè y=
1
12
−
x
x
1,00
1. TËp x¸c ®Þnh: R\{1}
2. Sù biÕn thiªn:
+ ChiÒu biÕn thiªn:
22 )1(
3
)1(
)12()1(2
'−
−
=
−
+
−
−
=xx
xx
y
Hµm sè nghÞch biÕn trªn c¸c kho¶ng (-∞; 1) vµ (1;+∞)
. Cùc trÞ : Hµm sè ®O cho kh«ng cã cùc trÞ
0,25
. TiÖm cËn:
−∞=
−
+
=
−
−
→
→
1
12
limlim
1
1
x
x
y
x
x
+∞=
−
+
=
+
+
→
→
1
12
limlim
1
1
x
x
y
x
x
Do ®ã ®−êng th¼ng x=1 lµ tiÖm cËn ®øng
2
1
12
limlim =
−
+
=
±∞→
±∞→
x
x
y
x
x
VËy ®−êng th¼ng y= 2 lµ tiÖm cËn ngang
0,25
* B¶ng biÕn thiªn:
x -∞ 1 +∞
y' - -
y 2
-∞
+∞
2
3* §å thÞ : HS tù vÏ ®å thÞ hµm sè.
0,5
I.2 Víi M bÊt k× ∈ (C), tiÕp tuyÕn t¹i M c¾t 2 tiÖm cËn t¹i A, B. T×m M ®Ó chu vi tam gi¸c
IAB ®¹t gi¸ trÞ nhá nhÊt.
1,00
Gäi M
−
+1
3
2;
0
0
x
x
∈(C)
* TiÕp tuyÕn t¹i M cã d¹ng:
1
3
2)(
)1(
3
0
0
2
0−
++−
−
−
=x
xx
x
y
C©u Néi dung §iÓm
TiÕp tuyÕn t¹i M c¾t hai tiÖm cËn t¹i A vµ B nªn täa ®é A; B cã d¹ng lµ: A
−
+1
6
2;1
0
x
B(2x
0
-1; 2) ; I(1; 2)
* Ta cã: S∆
IAB
=
2
1
. IA. IB=
63.212
1
6
2
1
0
0
==−⋅
−
⋅x
x
(®vdt)
0,25
0,25
* ∆IAB vu«ng cã diÖn tÝch kh«ng ®æi => chu vi ∆IAB ®¹t gi¸ trÞ nhá nhÊt khi IA= IB
(HS tù chøng minh).
−=
+=
⇒−=
−31
31
12
1
6
0
0
0
0
x
x
x
x
* VËy cã hai ®iÓm M tháa mOn ®iÒu kiÖn
M
1
(
32;31 ++
)
M
2
(
32;31 −−
)
Khi ®ã chu vi
∆
AIB =
6234 +
0,5
Câu Ý
Nội dung ðiể
m
II 2,00
1 1,00
1)
CâuII:2. Giải phương trình:
( )
(
)
3
sin 2 cos 3 2 3 os 3 3 os2 8 3 cos sinx 3 3 0
x x c x c x x
+ − − + − − =
.
3)sincos.3(833cos36cos.32cos.sin6cos.sin2
033)sincos.3(82cos.33cos.32)3(cos2sin
232
3
−−++−−+⇔
=−−+−−+
xxxxxxxx
xxxxxx
0)sincos3(8)sincos3(cos.6)sincos3(cos2
2
=−+−−−−⇔ xxxxxxxx
=
=
=
⇔
=−+
=−
⇔
=+−−−⇔
)(4cos
1cos
3tan
04cos3cos
0sincos3
0)8cos6cos2)(sincos3(
2
2
loaix
x
x
xx
xx
xxxx
Ζ∈
=
+=
⇔k
kx
kx ,
2
3
π
π
π
0,50
1 1,00
ðiều kiện:
| | | |
x y
≥
ðặt
2 2
; 0
u x y u
v x y
= − ≥
= +
;
x y
= −
không thỏa hệ nên xét
x y
≠ −
ta có
2
1
2
u
y v
v
= −
.
Hệ phương trình ñã cho có dạng:
0,25
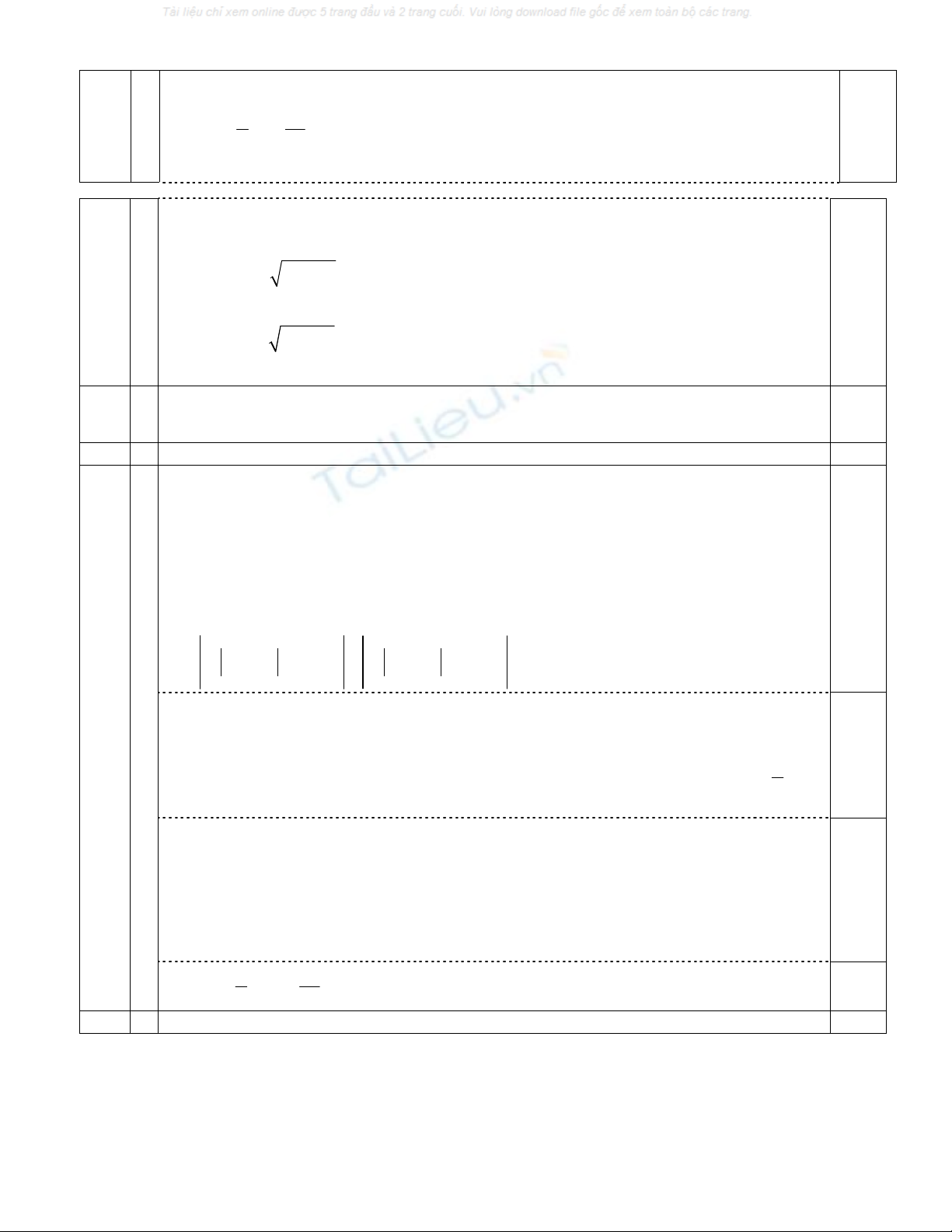
2
12
12
2
u v
u u
vv
+ =
− =
4
8
u
v
=
⇔
=
hoặc
3
9
u
v
=
=
+
2 2
4
4
88
ux y
vx y
=
− =
⇔
=+ =
(I)
+
2 2
3
3
99
ux y
vx y
=
− =
⇔
=+ =
(II)
0,25
Sau ñó hợp các kết quả lại, ta ñược tập nghiệm của hệ phương trình ban ñầu là
(
)
(
)
{
}
5;3 , 5;4
S=
1,00
III 0,25
Diện tích miền phẳng giới hạn bởi:
2
| 4 | ( )
y x x C
= − và
(
)
: 2
d y x
=
Phương trình hoành ñộ giao ñiểm của (C) và (d):
22 2
2 2
0 0
0
| 4 | 2 2
4 2 6 0
6
4 2 2 0
x x x
x x x x
x x x x x
x
x x x x x
≥ ≥
=
− = ⇔ ⇔ ⇔ =
− = − =
=
− = − − =
Suy ra diện tích cần tính:
( ) ( )
2 6
2 2
0 2
4 2 4 2
S x x x dx x x x dx
= − − + − −
∫ ∫
0,25
Tính:
( )
2
2
0
| 4 | 2
I x x x dx
= − −
∫
Vì
[
]
2
0;2 , 4 0
x x x
∀ ∈ − ≤
nên
2 2
| 4 | 4
x x x x
− = − +
⇒
( )
2
2
0
4
4 2
3
I x x x dx
= − + − =
∫
0,25
Tính
( )
6
2
2
| 4 | 2
K x x x dx
= − −
∫
Vì
[
]
2
2;4 , 4 0
x x x
∀ ∈ − ≤
và
[
]
2
4;6 , 4 0
x x x
∀ ∈ − ≥
nên
( ) ( )
4 6
2 2
2 4
4 2 4 2 16
K x x x dx x x x dx
= − − + − − = −
∫ ∫
.
0,25
Vậy
4 52
16
3 3
S= + =
1,00
IV 0,25
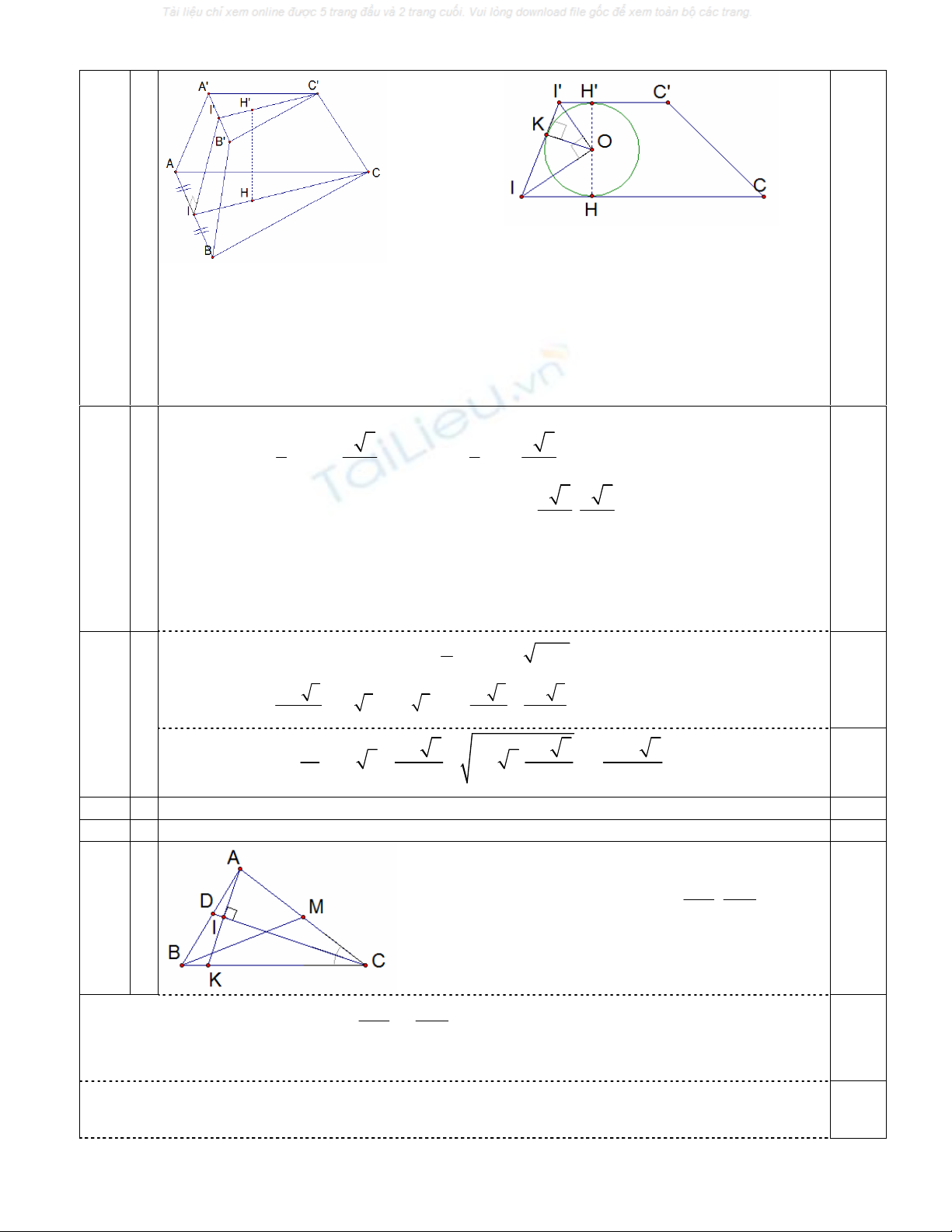
Gọi H, H’ là tâm của các tam giác ñều ABC, A’B’C’. Gọi I, I’ là trung ñiểm của AB,
A’B’. Ta có:
( ) ( ) ( )
' ' ' ' '
'
AB IC
AB CHH ABB A CII C
AB HH
⊥
⇒ ⊥ ⇒ ⊥
⊥
Suy ra hình cầu nội tiếp hình chóp cụt này tiếp xúc với hai ñáy tại H, H’ và tiếp xúc với
mặt bên (ABB’A’) tại ñiểm
'
K II
∈
.
0,25
Gọi x là cạnh ñáy nhỏ, theo giả thiết 2x là cạnh ñáy lớn. Ta có:
1 3 1 3
' ' ' ' ' ;
3 6 3 3
x x
I K I H I C IK IH IC= = = = = =
Tam giác IOI’ vuông ở O nên:
2 2 2 2
3 3
' . . 6r
6 3
x x
I K IK OK r x= ⇒ = ⇒ =
0,25
Thể tích hình chóp cụt tính bởi:
(
)
' . '
3
h
V B B B B
= + +
Trong ñó:
2 2 2
2 2
4x 3 3 3r 3
3 6r 3; ' ; 2r
4 4 2
x
B x B h
= = = = = =
0,25
Từ ñó, ta có:
2 2 3
2 2
2r 3r 3 3r 3 21r . 3
6r 3 6r 3.
3 2 2 3
V
= + + =
0,25
VIa 2,00
1
1,00
ðiểm
(
)
: 1 0 ;1
C CD x y C t t
∈ + − = ⇒ −
.
Suy ra trung ñiểm M của AC là 1 3
;
2 2
t t
M
+ −
. 0,25
ðiểm
( )
1 3
: 2 1 0 2 1 0 7 7;8
2 2
t t
M BM x y t C
+ −
∈ + + = ⇒ + + = ⇔ = − ⇒ −
0,25
0,25
Từ A(1;2), kẻ
: 1 0
AK CD x y
⊥ + − =
tại I (ñiểm
K BC
∈
).
Suy ra
(
)
(
)
: 1 2 0 1 0
AK x y x y
− − − = ⇔ − + =
.