PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
KIẾN XƯƠNG
*****
ĐỀ THI THỬ TUYỂN SINH VÀO LỚP 10 TRUNG HỌC PHỔ THÔNG
NĂM HỌC 2024 – 2025
Môn: Toán
(Thời gian làm bài: 120 phút)
Bài 1 (2,0 điểm).
1. Tính giá trị biểu thức
18 1 3 2 2−− −
2. Cho biểu thức:
x2 5 1
Px3x x6 x2
+
=−−
+ +− −
(với
x 0; x 4≥≠
)
a) Rút gọn P
b) Tìm tất cả các giá trị của x để
2
PP>
Bài 2 (2,0 điểm). Cho hệ phương trình
2
x my 3m
mx y m 2
+=
−= −
1) Giải hệ phương trình khi m = 3
2) Tìm m để hệ phương trình có nghiệm duy nhất (x; y) sao cho:
a) Điểm A(x; y) thuộc đường tròn tâm O bán kính
5
(Với O(0; 0) là gốc tọa độ).
b) x; y là độ dài hai đường chéo của hình thoi có chu vi là
cm.
Bài 3 (2,0 điểm).
Trên mặt phẳng tọa độ cho parabol (P): y =
2
x
và đường thẳng (d):
( )
y m2xm4=− + ++
a) Tìm tọa độ giao điểm của (d) và (P) khi m = - 4
b) Tìm m để (d) cắt (P) tại hai điểm phân biệt có hoành độ
12
x ;x
thỏa mãn:
12
x 0x<≤
Bài 4 (3,5 điểm).
1) Cho đường tròn tâm O và dây cung BC. Điểm A di chuyển trên cung lớn BC sao
cho tam giác ABC nhọn. Đường cao BE, CF của tam giác ABC cắt nhau tại H và cắt đường
tròn (O) theo thứ tự tại M, N.
a) Chứng minh tứ giác BCEF nội tiếp.
b) Chứng minh EF//MN và EF
⊥
OA.
c) Giả sử đường tròn (O) và dây BC cố định, xác định vị trí điểm A trên cung lớn BC
để diện tích tam giác AEH đạt giá trị lớn nhất.
2) Một bồn nước I-nox có dạng hình trụ với chiều cao 2m và chu vi đáy là
π
(m).
Hỏi bồn nước này đựng đầy được bao nhiêu mét khối nước? (Bỏ qua bề dày của vỏ
bồn nước và lấy
3,14π≈
).
Bài 5 (0,5 điểm).
Tìm giá trị nhỏ nhất của biểu thức:
1 4x 3
A 4x 2026
4x x 1
+
=+− +
+
với x > 0.
Hết
Họ và tên thí sinh:.........................................Số báo danh :........
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
KIẾN XƯƠNG
HƯỚNG DẪN CHẤM TUYỂN SINH VÀO LỚP 10 THPT
Năm học 2024 – 2025
Môn: Toán
Bài 1 (2,0 điểm)
3. Tính giá trị biểu thức
18 1 3 2 2−− −
4. Cho biểu thức:
x2 5 1
Px3x x6 x2
+
=−−
+ +− −
(với
x 0; x 4≥≠
)
a) Rút gọn P b) Tìm tất cả các giá trị của x để
2
PP>
Bài 1
(2,0 đ)
Câu1:
0,5đ
Ta có
18 1 3 2 2−− −
( )
2
9.2 1 2 1= −− −
321 21= −− −
0,25đ
( )
321 21= −− −
( vì
21>
)
32 1 2 1 22= −− +=
Vậy
18 1 3 22 22−− − =
0,25đ
Câu 2a
1,0đ
Ta có
x2 5 1
Px3x x6 x2
+
=−−
+ +− −
( )( )
x2 5 1
x3 x2
x3 x2
+
=−−
+−
+−
( )( ) ( )
( )( )
x2 x2 5 x3
x3 x2
+ − −− +
=+−
0,25đ
( )( ) ( )( )
x 4 5 x 3 x x 12
x3 x2 x3 x2
−−−− −−
= =
+− +−
0,25đ
( )( )
( )( )
x4 x3 x4
x2
x3 x2
−+ −
= = −
+−
0,25đ
Vậy khi
x 0; x 4≥≠
, thì
x4
Px2
−
=−
0,25đ
Câu2b
: 0,5đ
+ Ta có
x4
Px2
−
=−
với điều kiện
x 0; x 4≥≠
+ Để
2
PP>
thì
( )
PP 1 0−>
( )
( )
2
2 x4
x4 x4
. 10 0
x2 x2 x2
−−

−−
⇔ − >⇔ >

−−
 −
( )
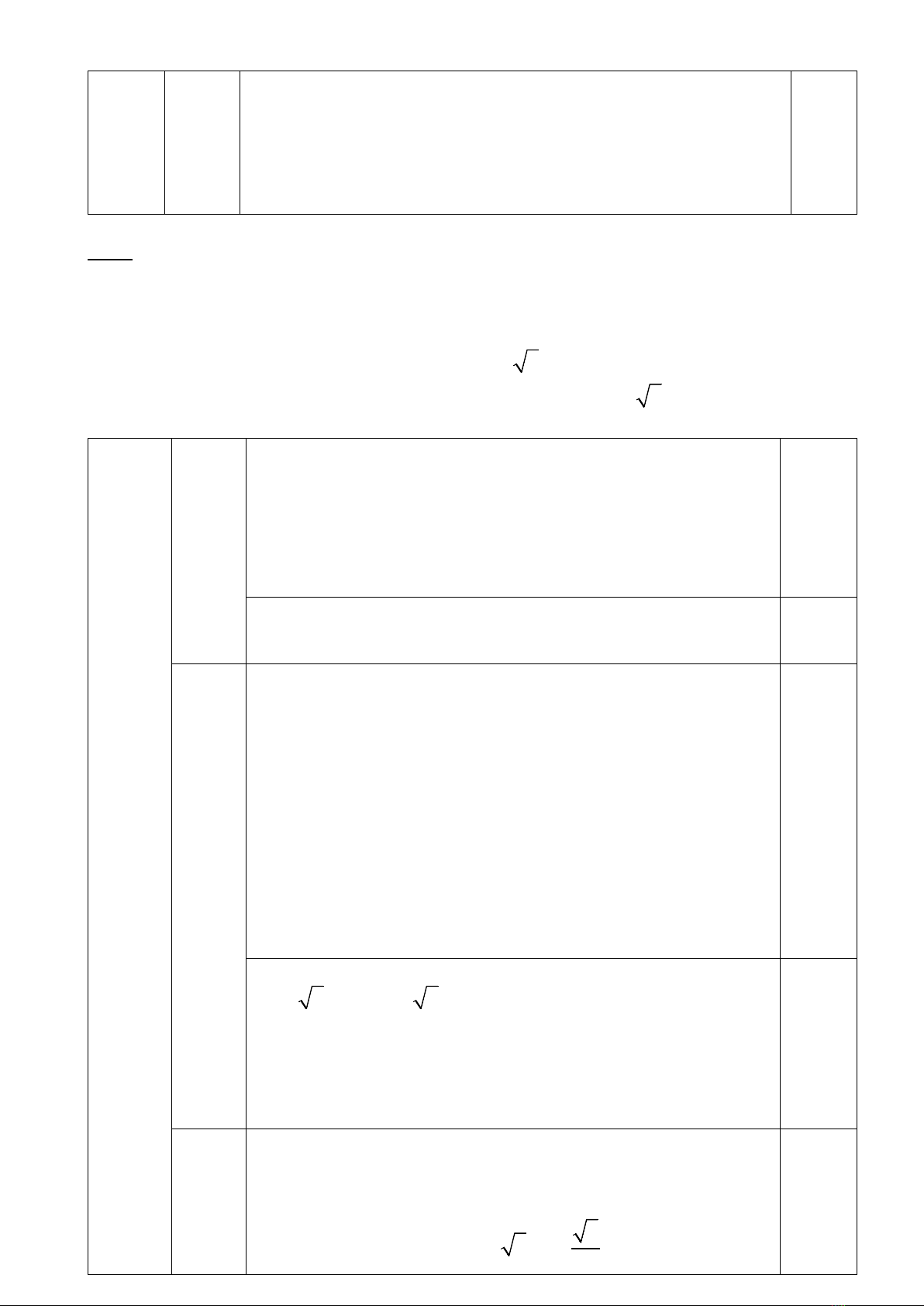
2 x4 0⇔− − >
( vì
( )
2
x 2 0x− >∀
tmđkxđ
0,25
đ
x 4 0 x 16⇔ −<⇔<
Két hợp với điều kiện ta được
0 x 16
x4
<<
≠
Vậy khi
0 x 16
x4
<<
≠
thì
2
PP>
(Không kết hợp điều kiện thì không cho điểm bước này)
0,25
Bài 2 (2,0 điểm) Cho hệ phương trình
2
x my 3m
mx y m 2
+=
−= −
1) Giải hệ phương trình khi m = 3
2) Tìm m để hệ phương trình có nghiệm duy nhất (x; y) sao cho:
a) A(x; y) thuộc đường tròn tâm O bán kính
5
(Với O(0; 0) là gốc tọa độ).
b) x, y là độ dài hai đường chéo của hình thoi có chu vi là
25
cm.
Bài 2
(2,0 đ)
Câu1:
0,75,đ
Với m = 3, hệ phương trình trở thành:
x 3y 9 x 3y 9 10x 30
3x y 7 9x 3y 21 x 3y 9
+= += =

⇔⇔

−= − = + =

x3 x3
3 3y 9 y 2
= =

⇔⇔

+= =

0,5
Vậy với m = 3 hệ phương trình có nghiệm là
x3
y2
=
=
0,25
Câu 2
0,75.đ
2
x my 3m (1)
mx y m 2 (2)
+=
−= −
+ Từ (1) => x = 3m – my (3)
Thế (3) vào (2) ta được: m(3m – my) - y = m2 – 2
3m2 – m2y – y = m2 – 2
– m2y – y = - 3m2 + m2 – 2
(m2 + 1)y = 2m2 + 2
(m2 + 1)y = 2(m2 + 1)
y = 2 (do (m2 + 1) > 0 với mọi m)
+ Thay y = 2 vào (3) ta được x = m
Vậy với mọi m, hệ phương trình luôn có nghệm duy nhất là
(x ; y) = (m; 2)
0,5
+ Ta có A(m ; 2). Để A(m ; 2) thuộc đường tròn tâm O bán
kính
5
thì OA =
5
OA2 = 5
m2 + 22 = 5
m2 = 1
m1= ±
Vậy
m1= ±
thỏa mãn đề bài
0,25
Câu 3:
0,5đ
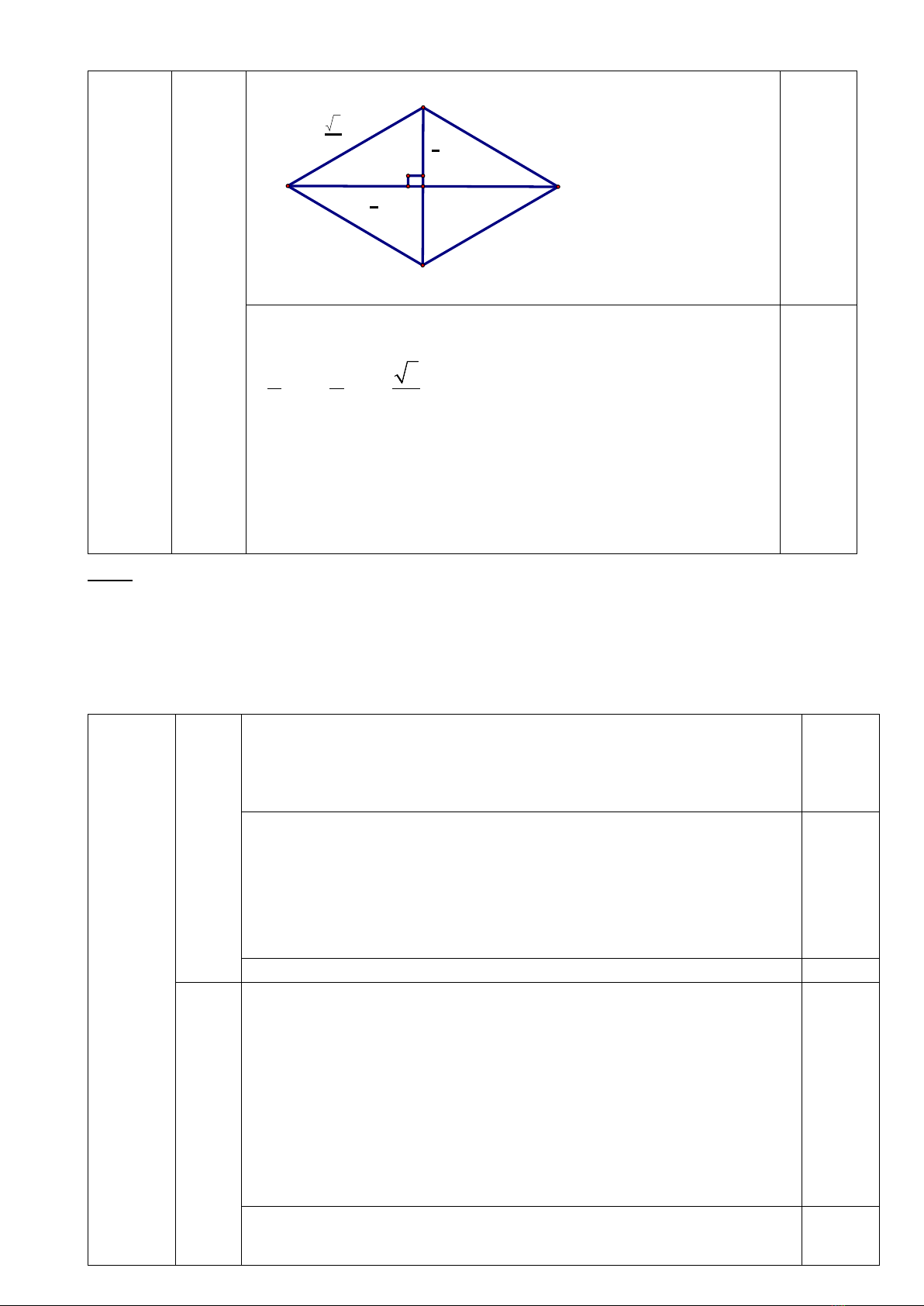
Do x, y là độ dài hai đường chéo của hình thoi nên
x0 m0 m0
y 0 2 0 (ld)
>>

⇔ ⇔>

>>

Độ dài cạnh của hình thoi là
5
2 5:4 2
=
0,25
5
2
y
2
x
2
O
D
C
B
A
Do hai đường chéo hình thoi vuông góc với nhau tại trung điểm
của mỗi đường nên ta có phương trình:
2
22
22
xy 5xy5
22 2

 
+ = ⇔+=

 
  
m2 + 22 = 5
m2 = 1
( )
( )
m 1 tm
m 1 ktm
=
= −
Vậy
m1=
thỏa mãn đề bài
0,25
Bài 3 (2,0 điểm)
Trên mặt phẳng tọa độ cho parabol (P): y =
2
x
và đường thẳng (d):
( )
y m2xm4=− + ++
a) Tìm tọa độ giao điểm của (d) và (P) khi m = - 4
b) Tìm m để (d) cắt (P) tại hai điểm phân biệt có hoành độ
12
x ;x
, thỏa mãn:
12
x 0x<≤
Bài 3
(2,0 đ)
Câu a
1đ
Thay m = - 4 vào (d) ta được:y = 2x
Khi đó phương trình hoành độ giao điểm của (d) và (P) là:
2
x 2x=
2
x 2x 0⇔−=
0,25
( )
xx 2 0⇔ −=
x0 x0
x20 x2
= =

⇔⇔

−= =

Với x = 0 => y = 0 => (0; 0)
Với x = 2 => y = 4 => (2; 4)
0,5
Vậy với m = - 4 thì tọa độ giao điểm của (d) và (P) là (0; 0); (2; 4)
0,25
Câu b
1đ
+ Phương trình hoành độ giao điểm của (d) và (P) là:
( )
( ) ( )
2
2
x m2xm4
x m 2x m 4 0 *
=− + ++
⇔ + + − −=
+ Tính được
( )
2
m 4 4 0m∆= + + > ∀
=> pt luôn có 2 nghiệm phân biệt
12
x ;x
với mọi m
+ Theo hệ thức Vi-ét, ta có
12
12
x x m2
x .x m 4
+ =−−
=−−
( )
( )
1
2
0,25
+ Để
12
x 0x<≤
ta xét 2 trường hợp sau:
TH1: Phương trình đã cho có 2 nghiệm
12
x ;x
thỏa mãn:
0,25
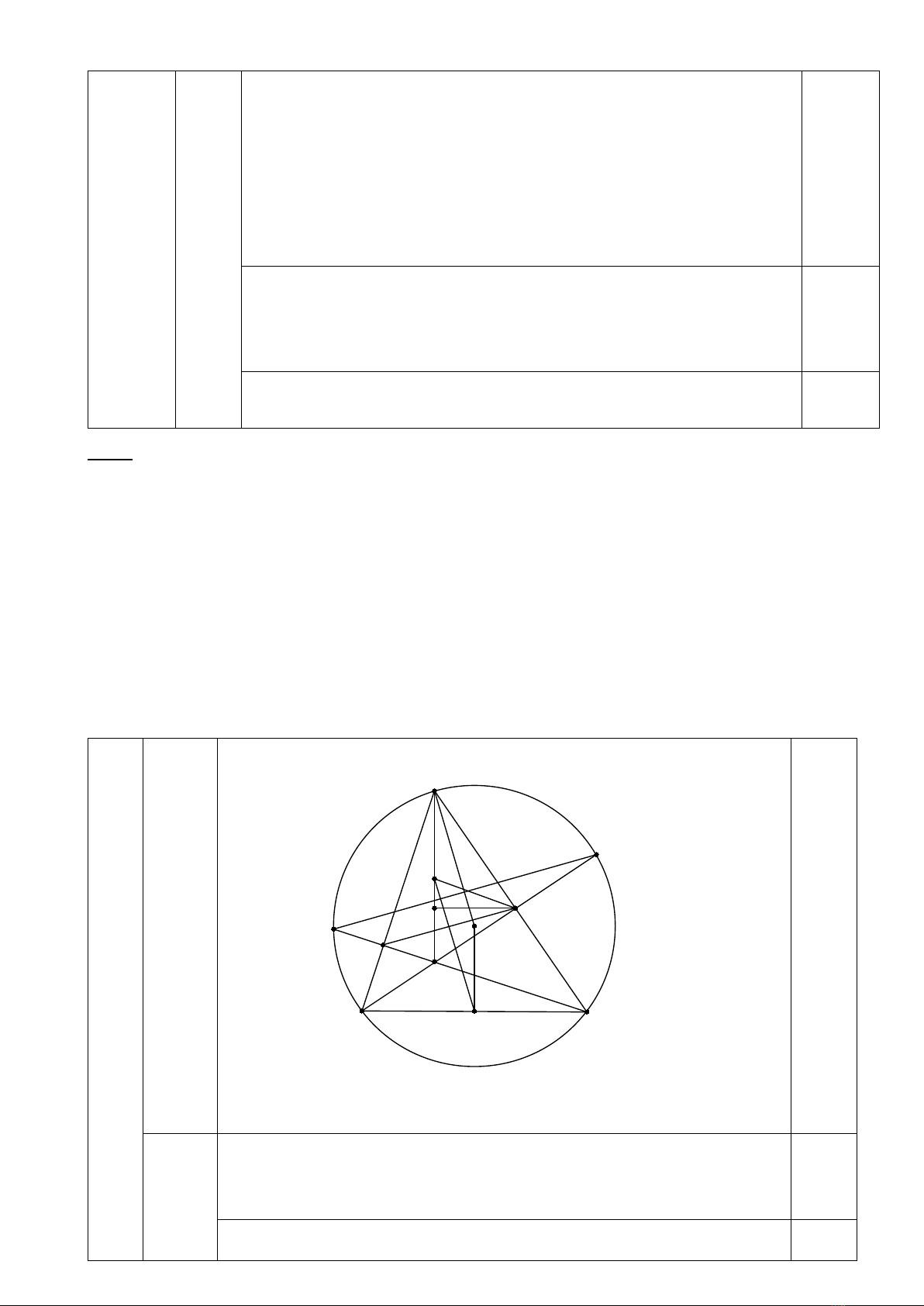
12
x 0; x 0<=
.
Thay x2 = 0 vào (2) ta được :
1
m 4 x .0−−=
m4⇔=−
Thay m = - 4;
2
x0=
vào (1), ta được
( )
11
x0 42 x2+=−− −⇔ =
Ta thấy
1
x 20= >
(không thỏa mãn
12
x 0; x 0<=
)
=> m = -4 (không tm)
Tr.h2: Phương trình đã cho có 2 nghiệm
12
x ;x
thỏa mãn
12
x 0x<<
=> phương trình đã cho có 2 nghiệm trái dấu
1.(- m - 4) < 0
m4⇔ >−
0,25
Vậy với m > - 4 để phương trình có 2 nghiệm
12
x ;x
, thỏa mãn:
12
x 0x<≤
0,25
Bài 4 ( 3,5 điểm)
1. Cho đường tròn tâm O và dây cung BC. Điểm A di chuyển trên cung lớn BC sao cho
tam giác ABC nhọn. Đường cao BE, CF của tam giác ABC cắt nhau tại H và cắt đường tròn
(O) theo thứ tự tại M,N
a) Chứng minh tứ giác BCEF nội tiếp. b) Chứng minh EF//MN và EF
⊥
OA.
c) Giả sử đường tròn (O) và dây BC cố định, xác định vị trí điểm A trên cung lớn BC để
diện tích tam giác AEH đạt giá trị lớn nhất.
2. Một bồn nước I-nox có dạng hình trụ với chiều cao 2m và chu vi đáy là
π
(m). Hỏi bồn
nước này đựng đầy được bao nhiêu mét khối nước? (Bỏ qua bề dày của bồn nước và lấy
3,14π≈
)
Bài
4
(3.5
đ)
Câu1a.
1,0đ
Xét tứ giác BCEF có:
0
BFC 90=
(CF
⊥
AB)
0
BEC 90=
(BE
⊥
AC)
0,5 đ
=>
( )
0
BFC BEC 90= =
0,25đ
H
E
F
O
A
B
C
M
N
K
I
D