Trang 1/2
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
HUYỆN GIAO THUỶ
ĐỀ CHÍNH THỨC
ĐỀ THI THỬ TUYỂN SINH
VÀO LỚP 10 THPT NĂM HỌC 2024 - 2025
MÔN: TOÁN
(Thời gian làm bài: 120 phút)
Đề thi thử gồm 02 trang.
Phần 1: Trắc nghiệm (2,0 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng
trước phương án đó vào bài làm
Câu 1. Điều kiện để biểu thức
1
2
x
x
có nghĩa là
A.
0
x
. B.
x
. C.
0, 4
x x
. D.
0; 4
x x
.
Câu 2. Đồ thị hàm số
2
2
y x
đi qua điểm nào trong các điểm sau?
A.
0;2
A. B.
1;2
B. C.
2; 8
C
. D. 1
;1
2
D
.
Câu 3. Hai đường thẳng
2
y mx
và
1 2 3
y m x
song song với nhau khi
A.
1
3
m
. B.
1
m
. C.
2
m
. D.
2
m
.
Câu 4. Trong các phương trình sau, phương trình nào có hai nghiệm trái dấu?
A. 2
2 3 2 0
x x
. B. 2
3 2 0
x x
.
C. 2
3 2 0
x x
. D. 2
5 6 0
x x
.
Câu 5. Số nghiệm của hệ phương trình
2 2
2 1
x y
y x
là
A.
0
. B.
1
. C. Vô số. D.
2
.
Câu 6. Cho hình trụ có chiều cao
h
và bán kính đáy
R
. Thể tích
V
của khối trụ được
tính bởi công thức
A.
2
1
3
V R h
. B.
2
V R h
. C.
2
V Rh
. D.
2
4
3
V R h
.
Câu 7. Trong mặt phẳng, cho đường tròn
;
O R
. Một đường thẳng
cắt đường tròn tại
hai điểm phân biệt
,
A B
sao cho
2 2
AB . Tính bán kính
R
của đường tròn biết khoảng
cách từ
O
đến
bằng
2
.
A.
3
R
. B.
2
R
. C.
1
R
. D.
4
R
.
Câu 8. Cho tam giác
ABC
có
3
AB AC
, gọi
,
M N
lần lượt là trung điểm của
AB
và
AC
. Biết
1
MN
, hãy tính chiều cao
h
của tam giác
ABC
kẻ từ đỉnh
A
.
A.
2
h. B.
10
h. C.
2
h
. D.
2 2
h.
Phần 2: Tự luận (8,0 điểm)
Câu 1. (1,5 điểm)
1) Chứng minh đẳng thức
7 4 3
2 3 3 2 2
3 2
.
2. Rút gọn biểu thức
1 1 1
.1
2 2 1
x
Ax
x x x x
với
0, 1x x
.
Câu 2. (1,5 điểm) Cho phương trình
22 1 0x x m
với
m
là tham số.
1) Giải phương trình khi
2m
.
2) Tìm các giá trị của
m
để phương trình có 2 nghiệm phân biệt
1 2
;x x
thỏa mãn
1 2
2 2
1 2 1 2
2 3 1
2
2( 1)
x x
x x x x
.
Câu 3. (1,0 điểm) Giải hệ phương trình
2 2
10
3
3 6
x y
y x
x y
.
Câu 4. (3,0 điểm)
1) Cho hình vuông
OABC
có
1OA cm
. Đường tròn tâm
B
, bán kính
BC
cắt tia
AB
tại
D
. Đường tròn tâm
A
, bán kính
AD
cắt tia
OA
tại
E
. Đường tròn tâm
O
, bán
kính
OE
cắt tia
CO
tại
F
. Đường tròn tâm
C
, bán kính
CF
cắt tia
OC
tại
H
.
a) Tính diện tích hình vuông
OABC
và hình quạt tròn
.ADE
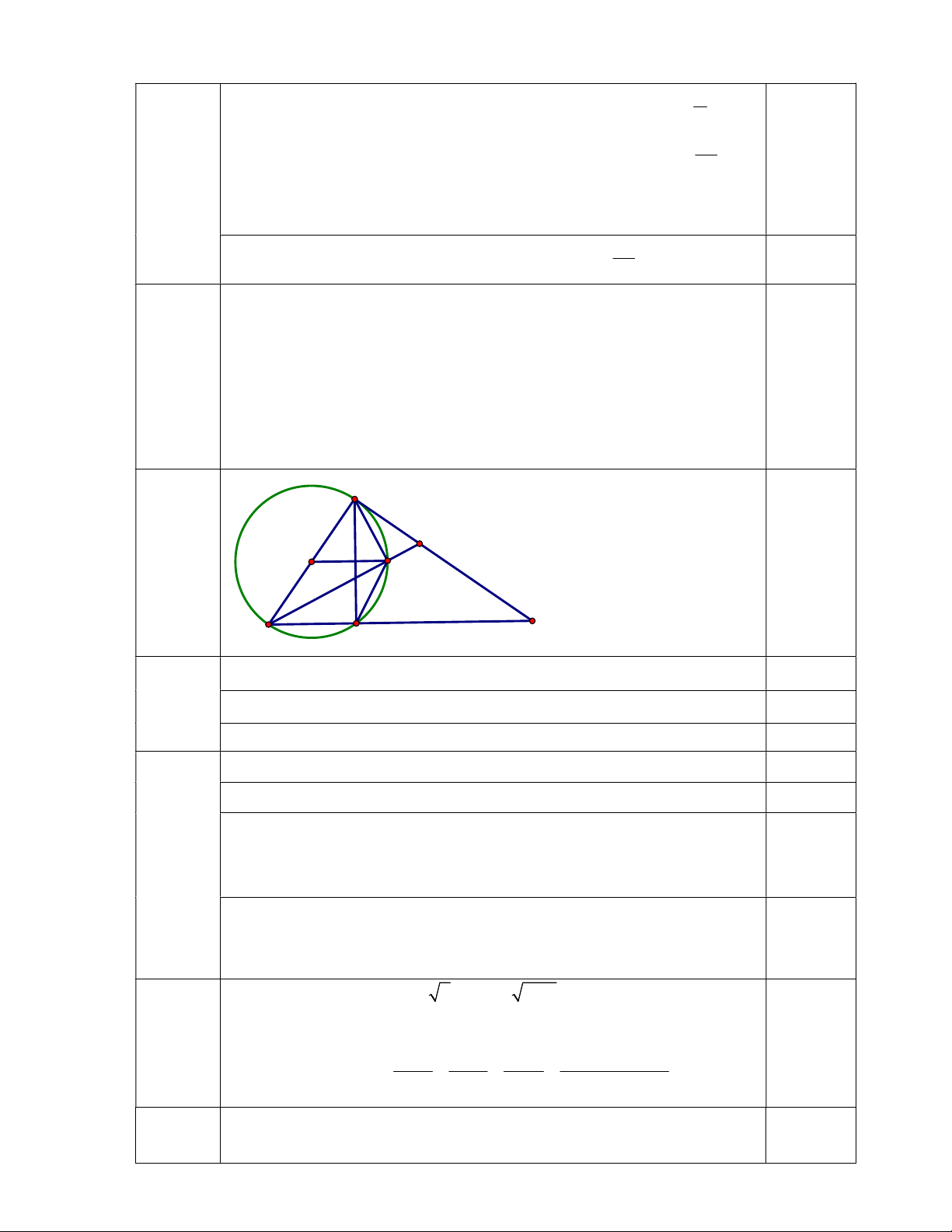
b) Tính diện tích phần tô đậm trong hình vẽ sau.
2) Cho tam giác
ABC
vuông tại
A
. Kẻ đường cao
AH
và đường phân giác trong
BD
của tam giác
ABC
,H BC D AC
. Đường thẳng đi qua
A
và vuông góc với
BD
cắt
BD
tại
E
.
a) Chứng minh rằng
ABHE
là tứ giác nội tiếp.
b) Gọi
;O R
là đường tròn ngoại tiếp tứ giác
ABHE
. Chứng minh
OE AH
.
Câu 5. (1,0 điểm)
1) Giải phương trình
2
4 1 5 2 10 5x x x x x x
.
2) Cho các số thực dương
, ,abc
thỏa mãn
3a b c
. Tìm giá trị nhỏ nhất của biểu
thức
2 2 2
2025
1 1 1 2
a b c
Pb c a ab ac bc
.
…………………Hết…………………..
Họ và tên thí sinh:…………………...... Họ tên, chữ kí GT 1...............................................
Số báo danh:…………........................... Họ tên, chữ kí GT 2..............................................
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
HUYỆN GIAO THỦY
HƯỚNG DẪN CHẤM
ĐỀ THI THỬ VÀO LỚP 10 THPT LẦN 2 MÔN
TOÁN NĂM HỌC 2024 – 2025
Phần 1. Trắc nghiệm (2,0 điểm) Mỗi đáp án đúng được 0,25 điểm
Câu 1 2 3 4 5 6 7 8
Đáp án D C A A B B B D
Phần 2. Tự luận (8,0 điểm)
Câu Hướng dẫn chấm Số điểm
Câu 1
1) Chứng minh đẳng thức
7 4 3
2 3 3 2 2
3 2
.
2. Rút gọn biểu thức
1 1 1
.
1
2 2 1
x
Ax
x x x x
với
0, 1
x x
.
1,5
1.1
Ta có
2
2 3
7 4 3
2 3 3 2 3 4
3 2 3 2
0,25
2 3 2 3
1 1 2
3 2 3 2
0,25
1.2
1 1 1
.
2 1
2 1 1
x
Ax x
x x x x
0,5
1 2
.
1
2
x x
x
x x
0,25
1
x
0,25
Câu 2
Cho phương trình 2
2 1 0
x x m
với
m
là tham số.
1) Giải phương trình khi
2
m
.
2) Tìm các giá trị của
m
để phương trình có 2 nghiệm phân biệt
1 2
;
x x
thỏa
mãn 1 2
2 2
1 2 1 2
2 3
1
2
2( 1)
x x
x x x x
.
1,5
2.1
Với
2
m
, phương trình trở thành 2
3 0
2
x x
0,25
Ta có
0
a b c
Chú ý : Có thể thay bước này bằng bước tính
0,25
nên phương trình có 2 nghiệm phân biệt 1 2
1; 3
x x
0,25
2.2 2
m
, phương trình có 2 nghiệm phân biệt
0 2 0 2
m m
0,25
Khi đó, theo Viet ta có
1 2
1 2
2
1
x x
x x m
.
1 2
2 2 2
1 2 1 2 1 2 1 2
2 1 3
2 3
2( 1) 4 2
2 1 2 1
4 4 1 2 6 4
m
x x
x x x x x x x x
m m
m m
0,25
Từ giả thiết ta có
2 1 1 1
2 1 3 2 4 2
6 4 2 2
mm m m m
m
, thỏa
mãn
0,25
Câu 3 Giải hệ phương trình
2 2
10 (1)
3
3 6 (2)
x y
y x
x y
. 1,0
Điều kiện
0, 0x y
.
Đặt , 0
xt t
y , phương trình (1) trở thành
2
3
1 10 3 10 3 0 1
33
t
t t t
tt
.
0,25
Với
3 3t x y
, thay vào phương trình (2) ta được
2
1 3
11 3
y x
yy x
0,25
Với
13
3
t y x
, thay vào phương trình (2) ta được: 2
26 6x
, vô lý 0,25
Vậy hệ phương trình có các nghiệm
3;1 ; 3; 1
. 0,25
Câu 4.1
1) Cho hình vuông OABC có 1OA cm
. Đường tròn tâm B, bán kính
BC cắt tia AB tại D. Đường tròn tâm A, bán kính AD cắt tia OA tại
E
.
Đường tròn tâm O, bán kính OE cắt tia CO tại F. Đường tròn tâm
C
,
bán kính CF cắt tia OC tại H. Tính diện tích phần tô đậm trong hình vẽ
sau.
1,0
Hình vuông OABC có cạnh bằng 1cm nên có diện tích
2
11S cm
0,25
Hình quạt tròn ADE có bán kính bằng 2cm nên có diện tích
2
2
S cm
0,25
Hình quạt tròn
BCD
có bán kính bằng
1
cm
nên có diện tích
2
3
4
S cm
Hình quạt tròn
OEF
có bán kính bằng
3
cm
nên có diện tích
2
4
9
4
S cm
Đường tròn tâm
C
bán kính
4
CF cm
nên nửa hình tròn có diện tích
2
58
S cm
0,25
Vậy diện tích phần tô đậm:
2
5 4 3 2 1
91
2
S S S S S S cm
0,25
Câu 4.2
Cho tam giác
ABC
vuông tại
A
. Kẻ đường cao
AH
và đường phân giác
trong
BD
của tam giác
ABC
,
H BC D AC
. Đường thẳng đi qua
A
và vuông góc với
BD
cắt
BD
tại
E
.
a) Chứng minh rằng
ABHE
là tứ giác nội tiếp.
b) Gọi
;
O R
là đường tròn ngoại tiếp tứ giác
ABHE
. Chứng minh
OE AH
.
2,0
4.2.a
0
90 (1)
AH BC AHB 0,25
0
90 (2)
AE BD AEB 0,25
Từ (1) và (2) suy ra
ABHE
là tứ giác nội tiếp đường tròn đường kính
AB
0,5
4.2.b
ABD AHE
(cùng chắn cung
AE
) 0,25
CBD HAE
(cùng chắn cung
HE
) 0,25
ABD CBD
(do
BD
là phân giác)
EAH HAE
, do đó tam giác
AEH
cân tại
E
.
EA EH
nên
E
nằm trên đường trung trực của
AH
.
0,25
Đường tròn
,
O R
ngoại tiếp tứ giác
ABHE
nên
O
là trung điểm của
AB
và
OA OH
, do đó
O
nằm trên đường trung trực của
AH
.
Từ đó suy ra
OE AH
.
0,25
Câu 5
1) Giải phương trình
2
4 1 5 2 10 5
x x x x x x
.
2) Cho các số thực dương
, ,
abc
thỏa mãn
3
abc
. Tìm giá trị nhỏ
nhất của biểu thức
2 2 2
2025
1 1 1 2
a b c
P
b c a ab ac bc
.
1,0
5.1 Điều kiện
0 5
x
.
Khi đó ptr 0,25
O
E
D
H
B
A
C