PHÒNG GD&ĐT NAM ĐÀN
KY THI THỬ TUYỂN SINH VÀO LỚP 10 THPT
NĂM HỌC: 2024 – 2025
Môn thi: Toán
Thời gian làm bài: 120 phút
Khóa thi ngày:08/5/2024
Câu 1. (2,5 điểm)
a) Tính: A =
9
2 9 3 0, 25 116
+−
b) rút gọn biểu thức B =
14 7
49
77
xx
x
xx
−−
−
−+
với
0, 49xx≥≠
c) Xác định hàm số bậc nhất biết đồ thị của nó đi qua điểm M(-1; -5) và và điểm N(1;1)
Câu 2. (2,0 điểm)
a) Giải phương trình: x2 + x - 6 = 0
b) Cho phương trình x2 – 5x + 1 = 0 có hai nghiệm dương phân biệt x1, x2. Không giải
phương trình, hãy tính giá trị của biểu thức: M =
12
12
xx
xx
−
+
Câu 3. (2,0 điểm).
1. Hai xe ô tô khởi hành cùng một lúc từ hai địa điểm A và B cách nhau 100 km. Xe thứ nhất
chạy nhanh hơn xe thứ hai 10km/h nên đến nơi trước xe thứ hai 30 phút. Tính vận tốc mỗi
xe?
2. Một hình nón được đặt vào bên trong một hình lập
phương có cạnh bằng 1 dm (như hình vẽ).
Tính thể tích hình nón? (với
3,14
π
=
)
Câu 4. (3.0 điểm) Cho tam giác ABC nhọn (AB < AC)
nội tiếp đường tròn (O). Tiếp tuyến tại A của (O) cắt
tia CB tại S. Gọi I là trung điểm của BC.
a) Chứng minh tứ giác SAOI nội tiếp
b) Vẽ AH vuông góc với SO tại H, Tia AH cắt BC tại K. Chứng minh: SH.SO = SK.SI
c) Chứng minh:
SK SC
SB SI
=
d) Vẽ đường kính PQ đi qua điểm I (P thuộc cung nhỏ AC). SP cắt đường tròn (O) tại điểm
thứ hai là M. Chứng minh PK vuông góc với SQ
Câu 5. (0,5 điểm) Giải phương trình:
----------------Hết-----------------
Chú ý: Giám thị không giải thích gì thêm
Họ và tên thí sinh: ………………….………………………Số báo danh: ………………….
ĐỀ CHÍNH THỨC
Đáp án và biểu điểm môn Toán 9
Câu
Ý
Nội dung
Điểm
1
a.
1,0 đ
9
2 9 3 0, 25 116
+−
= 2.3 +3.0,5 -
25
16
= 6 +
3
2
-
5
4
= 6 +
1
4
=
25
4
0,5
0,5 đ
b
0,75đ
B =
14 7
49
77
xx
x
xx
−−
−
−+
B =
.( 7) 14 7( 7)
( 7)( 7) ( 7)( 7) ( 7)( 7)
xx x x
xx xx xx
+−
−−
+− +− +−
0,25
B =
7 14 7 49
( 7)( 7)
xx xx
xx
+− −+
+−
0,25
B=
2
( 7)
( 7)( 7)
x
xx
−
=+−
=
7
7
x
x
−
=+
0,25
c
0,75đ Gọi công thức hàm số cần tìm là: y = ax + b (a
≠
0) (d)
Do (d) đi qua điểm M(-1; -5) nên -a + b = -5 (1)
0,25
Do (d) đi qua điểm M(1; 1) nên a + b = 1 (2)
0,25
Từ (1) và (2) tìm được a = 3, b = -2 nên hàm số bậc nhất cần tìm là y =3x - 2
0,25
2
a
(1,0
đ)
x2 +x - 6 = 0
Ta có:
∆
= b2 – 4ac = 12 – 4.1.(-6) = 25 >0
0,5
Nên phương trình có hai nghiệm phân biệt
x1 =
2
b
a
−+ ∆
=
1 25
2.1
−+
= 2
x2 =
2
b
a
−− ∆
=
1 25
2.1
−−
= -3
0,25
0,25
b
1,0 đ Cho phương trình x2 – 5x + 1 = 0 có hai nghiệm dương phân biệt x1, x2.
Không giải phương trình, hãy tính giá trị của biểu thức: M =
12
12
xx
xx
−
+
Theo định lý Vi – Ét ta có:
12
12
5
.1
b
xx a
c
xx a
+ =−=
= =
Ta có M =
( )( )
1212
12
12 12
xx xx
xx
xx xx
+−
−=
++
12
Mxx= −
( )
2
2
1 2 1 2 12
2 . 5 2.1 3M x x x x xx= − =+− =− =
⇒
12
Mxx= −
=
3
vì M > 0
0,25
0,25
0,25
0,25
2
3
1
1,5 đ
Gọi vận tốc xe thứ nhất là x (km/h) ĐK: x > 10
0,25
Vận tốc xe thứ hai là: x - 10 (km/h)
0,25
Thời gian xe thứ nhất đi hết
quãng đường AB là
100
x
(h)
Thời gian xe thứ hai đi hết quãng đường AB là:
100
10x−
(h)
0,25
Do xe thứ nhất chạy nhanh hơn xe thứ hai 10km/h nên đến nơi trước xe thứ
hai 30 phút =
1
2
giờ nên ta có phương trình
100
10x−
-
100
x
=
1
2
0,25
⇒
x2 – 10x – 2000=0
x1 =
5 2025
1
+
= 50 (TMĐK)
x2 =
5 2025
1
−
= -40 (loại)
0,25
Vậy vận tốc xe thứ nhât là 50 km/h
Vận tốc xe thứ hai là 50 – 10 = 40 km/h
0,25
b
0,5đ
Từ hình vẽ ta có:
Hình nón có chiều cao bằng cạnh hình lập phương bằng 1 dm.
Bán kính đáy bằng nửa cạnh hình lập phương bằng 0,5 dm
0,25
Nên thể tích hình nón là V =
2
1
3Rh
π
≈
2
1.3,14.(0,5) .1
3
≈
0,26 dm3 0,25
Câu
4.
3,0
điểm
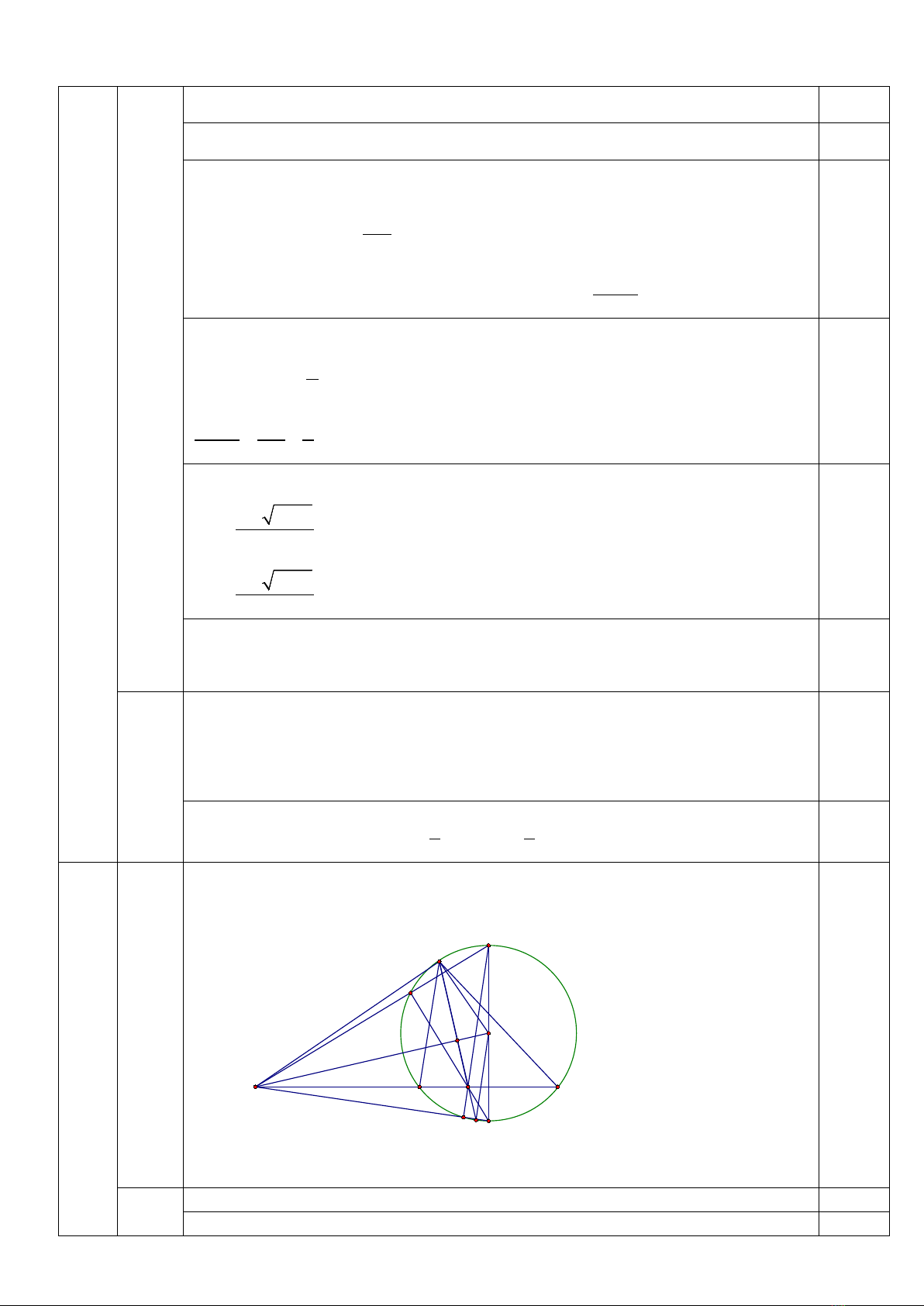
Vẽ hình đúng cho câu a) cho 0,5 điểm
Vẽ hình sai hoặc không vẽ hình: Không chấm điểm bài hình
0,5
a.
1,0
Chứng minh tứ giác SAOI nội tiếp
Ta có: OI
⊥
BC ( Đường kính đi qua trung điểm của dây không đi qua tâm)
0,25
D
K
I
H
O
M
P
Q
C
B
A
S
3
0
SIO 90
0
SAO 90
(theo t/c của tiếp tuyến)
0,25
00 0
SIO SAO 90 90 180 
0,25
Tứ giác SAOI nội tiếp được một đường tròn
0,25
b
0,5đ
Xét
SHK và
SIO có
OSI
chung;
0
SHK SIO 90
SHK SIO
(g. g)
0,25
Suy ra
SH SK
SI SO
⇒
SH.SO = SK.SI (1) 0,25
c
0,5đ
Áp dụng hệ thức lượng vào tam giác SAO vuông tại A, đường cao AH có:
SA2 = SH.SO (2)
Xét
SAB và
SCA có
ASC
chung;
SAB SCA
(cùng chắn cung AB)
SAB SCA
(g. g)
⇒
SA SB
SC SA
⇒
SA2 = SB.SC (3)
0,25
Từ (1) và (2) và (3) suy ra SK.SI = SB.SC
⇒
SK SC
SB SI
=
0,25
d.
0,5
d) Vẽ đường kính PQ đi qua điểm I (P thuộc cung nhỏ AC). SP cắt đường
tròn (O) tại điểm thứ hai là M. Chứng minh M, K, Q thẳng hàng
Tương tự câu c) ta cũng chứng minh được SA2 = SM.SP
⇒
SM.SP = SK.SI
⇒
SK SM
SP SI
=
SKM SPI
(c-g-c)
⇒
0
SMK SIP 90
⇒
KM
⊥
SP (4)
0,25
Lại có:
0
PMQ 90
(góc nội tiếp chắn nửa đường tròn)
⇒
QM
⊥
SP (5)
Từ (4) và (5) M, K, Q thẳng hàng
⇒
K là trực tâm của tam giác SPQ
⇒
PK
⊥
SQ
0,25
5
0,5 đ
Giải phương trình:
(1)
ĐK: x
5
2
≥
Đặt
25xy−=
≥
0
⇔
2
25
25 2
y
yx x +
= −⇔ =
Ta có (1)
⇔
22
55
2 3 2 22
22
yy
yy
++
++ + −− =
⇔
22
6 9 2 14yy yy+++ −+=
⇔
3 14yy++ −=
0,25
4
⇔
3 14yy++ −=
Do y + 3>0
⇔
11yy−=−
⇔
11yy−=−
⇔
1 – y
≥
0
⇔
y
≤
1
Kết hợp ĐK ta có 0
≤
y
≤
1
⇔
0 2 51x≤ −≤
⇔
02 51x≤ −≤
⇔
53
2x≤≤
Kết hợp ĐKXĐ ta có S =
5
/3
2
xx

∈ ≤≤


0,25
Chú ý: HS giải cách khác đúng vẫn cho điểm tối đa.