PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
NGHI LỘC
(Đề thi gồm có 01 trang)
KỲ THI THỬ TUYỂN SINH VÀO LỚP 10 THPT
NĂM HỌC 2024 - 2025
Môn thi: TOÁN
Thời gian làm bài: 120 phút, không kể thời gian giao đề
Câu 1 (2,5 điểm).
a) Tính giá trị biểu thức:
1
18 4. 8 50.
5
A
b) Rút gọn biểu thức:
3 1 9
.
33
x
Bx x x x





với
0; 9.xx
c) Tìm giá trị của tham số
m
để đường thẳng
21y m x m
song song với
đường thẳng
.
Câu 2 (2,0 điểm).
a) Giải phương trình:
23 0.52xx
b) Cho phương trình
24 12 0xx
có hai nghiệm phân biệt
12
;.xx
Không
giải phương trình, hãy tính giá trị của biểu thức:
12
2
12
.
2 24 4
xx
Txx

Câu 3 (2,0 điểm). a) Một thửa ruộng hình chữ nhật có diện tích 900m2. Nếu chiều
dài giảm 2 lần, chiều rộng tăng thêm 30m thì chu vi thửa ruộng không thay đổi.
Tính chiều dài và chiều rộng thửa ruộng.
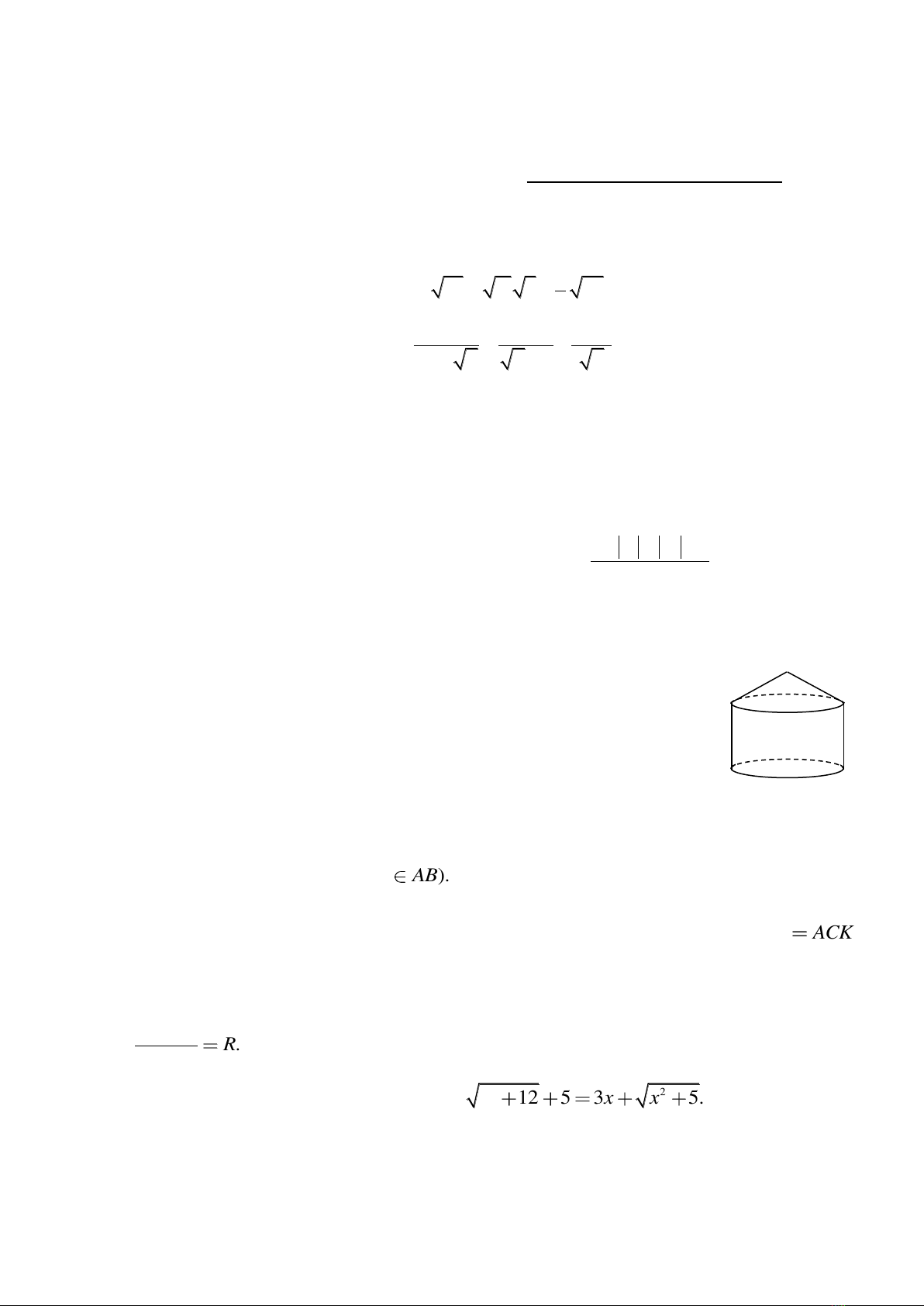
b) Một chi tiết máy gồm một phần có dạng hình trụ, phần
còn lại có dạng hình nón (hình bên). Biết rằng phần hình trụ có
chu vi đáy bằng 31,4cm và chiều cao 6cm; phần hình nón có
chiều cao 3cm. Tính thể tích của chi tiết máy đó (lấy
3,14;
kết quả làm tròn đến chữ số thập phân thứ 2).
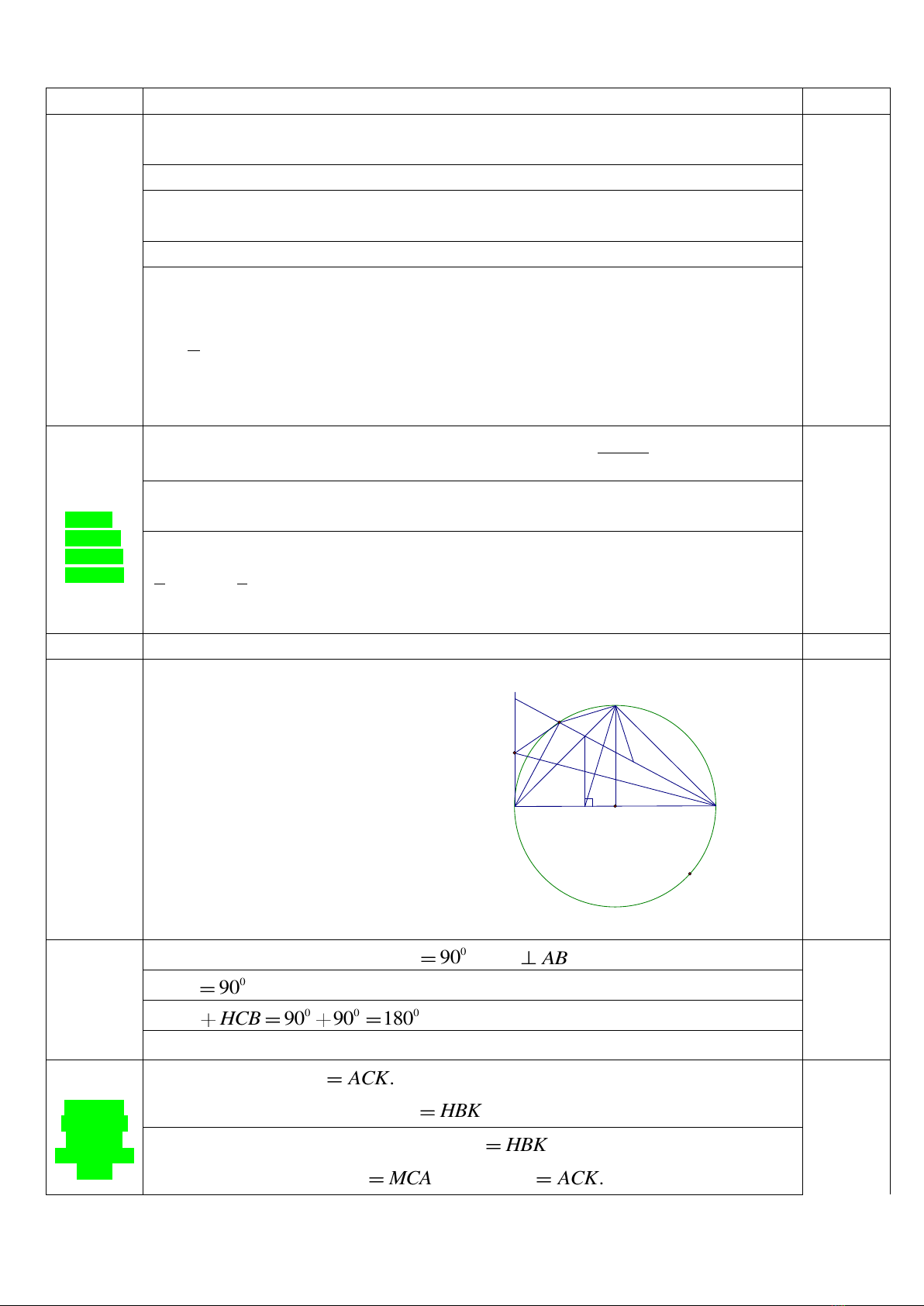
Câu 4 (3,0 điểm). Cho đường tròn (O, R), đường kính AB. Bán kính OC vuông góc
với AB, M là điểm bất kỳ trên cung nhỏ AC (M khác A và C), BM cắt AC tại H.
Kẻ HK vuông góc với AB
( ).K AB
a) Chứng minh CBKH là tứ giác nội tiếp.
b) Trên đoạn thẳng BM lấy điểm E sao cho BE = AM. Chứng minh
ACM ACK
và tam giác ECM là tam giác vuông cân tại C.
c) Gọi d là tiếp tuyến của đường tròn (O) tại điểm A. Cho P là một điểm nằm
trên d sao cho hai điểm P và C nằm trong cùng một nửa mặt phẳng bờ AB và
..
AP MB R
MA
Chứng minh đường thẳng PB đi qua trung điểm của đoạn thẳng HK.
Câu 5 (0,5 điểm). Giải phương trình:
22
12 5 3 5.x x x
.......................... Hết .......................
Họ và tên thí sinh: ....................................................... Số báo danh: ........................
HƯỚNG DẪN CHẤM
ĐỀ THI THỬ TUYỂN SINH VÀO LỚP 10 THPT, NĂM HỌC 2024-2025
Môn: TOÁN
Câu
Hướng dẫn chấm
Điểm
Câu 1
2,5đ
a) 1,0đ
Ta có:
1
18 4. 8 50
5
A
3 2 4 2 2
0,75đ
62
0,25đ
b) 1,0đ
3( 3) ( 3) 9
.
( 3)( 3) ( 3)( 3)
x x x x
Bx x x x x x x




0,25đ
3 9 3 ( 3)( 3)
.
( 3)( 3)
x x x x x
Bx x x x

0,5đ
( 9) .
x
Bx

0,25đ
c) 0,5đ
Để đường thẳng
21y m x m
song song với đường thẳng
52yx
phải có:
215
2
m
m

0,25đ
2
2
m
m

2m
. Vậy
2m
0,25đ
Câu 2
2,0đ
a) 1,0đ
24b ac
2
5 4.2.( 3) 49 0
0,25đ
49 7.
(Có thể HS không cần tính nếu trong khi tính nghiệm đưa ý này vào)
0,25đ
Phương trình đã cho có 2 nghiệm phân biệt:
1
5 7 1
2 2.2 2
b
xa
0,25đ
2
57 3
2 2.2
b
xa
0,25d
b) 1,0đ
Theo hệ thức Viet ta có:

12
12
12
4
xx
xx
12
0, 0xx
0,25đ
=>
1 2 1 2
x x x x
= 12 (HS có thể tính
12
xx
bằng cách bình phương).
0,25đ
x1 là nghiệm của phương trình đã cho nên ta có: x1
2 - 12x1 + 4 = 0 => x1
2 = 12x1 - 4
=> 2x1
2 = 24x1
- 8
0,25đ
=> 2x1
2 + 24x2
- 4 = 24x1 - 8 + 24x2 - 4 = 24(x1 + x2) - 12 = 24.12 - 12 = 276.
Vậy
12 1 .
276 23
T
0,25đ
(Tính đúng được mỗi hạng tử: 0,25đ)
Có thể HS không cần viết
(HS có thể không cần viết công thức nghiệm
(Ý này không cần nếu trong khi tính giá trị biểu thức thay đúng)
Câu 3
2,0đ
a) 1,25đ
Gọi chiều dài, chiều rộng thửa ruộng hình chữ nhật lần lượt là x, y (đơn
vị: m; x, y > 0)
0,25đ
Theo bài ra ta có phương trình: x. y = 900 (1)
0,25đ
Chiều dài thửa ruộng sau khi giảm 2 lần: x/2 (m)
Chiều rộng thửa ruộng sau khi tăng thêm 30m: y + 30 (m)
0,25đ
Theo bài ra ta có phương trình: 2(x/2 + y + 30) = 2(x + y) (2)
0,25đ
Từ (1) và (2) ta có hệ phương trình:
. 900
2.( 30) 2.( )
2
xy
xy x y
Giải hệ phương trình tìm được: x = 60, y = 15 (thoả mãn điều kiện)
Vậy, thửa ruộng có chiều dài 60m, chiều rộng 15m.
0,25đ
b) 0,75đ
Độ dài bán kính đáy của phần hình trụ là:
31,4 5
2.3,14
R
(cm)
0,25đ
Thể tích chi tiết máy của phần có dạng hình trụ là: V1 =
2.Rh
=
3,14.52.6 = 471 (cm3) (*)
0,25đ
Thể tích của chi tiết máy của phần có dạng hình nón là: V2 =
22
11
. .3,14.5 .3 78,5
33
Rh

(cm3) (**)
Thể tích của chi tiết máy đó là: V = V1 + V2 = 471 + 78,5 = 549,5 (cm3)
0,25đ
Câu 4
3,0đ
0,5đ
0,5 đ
a) 1,0đ
Xét tứ giác CBKM ta có:
0
90BKH
(
HK AB
)
0,25đ
0
90HCB
(Góc nội tiếp chắn nửa đường tròn)
0,25đ
0 0 0
90 90 180BKH HCB
0,25đ
Mà 2 góc này ở vị trí đối nhau. Suy ra tứ giác CBKH nội tiếp.
0,25đ
b) 1,0đ
(HS có thể
chứng minh
(**) trước
(*): 0,25đ cho
ý này)
- Chứng minh
.ACM ACK
Tứ giác CBKH nội tiếp nên
HCK HBK
(2 góc nội tiếp cùng chắn cung HK) (*)
0,25đ
Tứ giác ABCM nội tiếp (O) nên
MCA HBK
(2 góc nội tiếp cùng chắn
cung AM) (**) =>
HCK MCA
hay
.ACM ACK
0,25đ
(HS tính
(**) trước
(*): 0,25 đ
cho ý này)
Vẽ hình đến câu a: 0,25đ
Không vẽ hình thì không
chấm bài hình
Q
P
N
d
E
K
H
M
O
C
B
A
- Chứng minh
ECM
vuông cân tại C.
Vì
CO AB
nên CO là trung trực của AB => CA = CB
Xét
AMC
và
BEC
có
MAC MBC
(2 góc nội tiếp cùng chắn cung MC)
MA = BE (gt), CA = CB (cmt) (1) =>
AMC BEC
(c.g.c)
0,25đ
=>
ACM ECB
(2 góc tương ứng) và CM = CE (2 cạnh tương ứng)
Mặt khác
0
90ECB ECA
=>
0
90MCA ECA MCE
(2)
Từ (1) và (2) =>
ECM
vuông cân tại C.
0,25đ
c) 0,5đ
Theo gt
.AP MB R
MA
=>
AP R BO
AM MB BM
Lí giải được
PAM ABM
(sđ = 1/2 cung AM)
=>
PAM OBM
(c.g.c) =>
1
PA OB
PM OM
=> PA = PM
Vậy cần lấy điểm P thuộc d sao cho PA = PM
Gọi N là giao điểm của BP và HK, Q là giao điểm của BM với d
Xét
QMA
vuông tại M có: PA = PM =>
PMA
cân tại P
=>
PAM PMA
Lí giải được
0
90PMA PMQ
và
0
90PAM PQM
=>
PMQ PQM
=>
PMQ
cân tại P => PM = PQ (2)
0,25đ
Từ (1) và (2) => PM = PA = PQ
Vì AQ //HK (cùng vuông góc với AB)
Chứng minh được
NK NH
PA PQ
(cùng bằng
BN
BP
)
Mà PA = PQ (cmt) => NK = NH => N là trung điểm của HK
Vậy, với P d mà
.AP MB R
MA
thì PB đi qua trung điểm của HK.
0,25đ
Câu 5
0,5đ
0,5đ
Điều kiện: Mọi
.xR
Phương trình đã cho tương đương với
22
12 4 3 6 5 3x x x
22
22
44
3( 2)
12 4 5 3
xx
x
xx
22
22
( 2) 3 0
12 4 5 3
xx
x
xx
(*)
0,25đ
Ta có
22
3 5 12 5 0x x x
nên để phương trình có nghiệm thì
5.
3
x
Với x > 5/3 ta có x + 2 > 0.
Mặt khác
22
12 4 5 3 0xx
nên
22
22
3 0.
12 4 5 3
xx
xx
Từ (*) suy ra x - 2 = 0 <=> x = 2 (TM). Vậy phương trình đã cho có 1 nghiệm x = 2.
0,25đ
Lưu ý:
- Trên đây chỉ mang tính hướng dẫn chấm.
- Học sinh làm đúng, chặt chẽ mới cho điểm tối đa.
- Học sinh làm cách khác đúng thì cho điểm tương ứng.