TỦ SÁCH LUYỆN THI
ＴＸ＠Đ󰹡＠ｔｈｉ＠ｔｕｙ󰹣ｎ＠ｓｉｎｈ＠ｖ￀ｏ＠ｌ󰹻ｐ＠ＱＰ＠ｃｈｕｙￊｎ＠ｔｏ￁ｎ
ｎĂｍ＠ｈ󰹭ｃ＠ＲＰＱＹ＠Ｍ＠ＲＰＲＰ
SỞ GIÁO DỤC VÀ ĐÀO TẠO
BẠC LIÊU
ĐỀ TUYỂN SINH LỚP 10 THPT CHUYÊN
NĂM HỌC 2019-2020
Môn thi chuyên: TOÁN
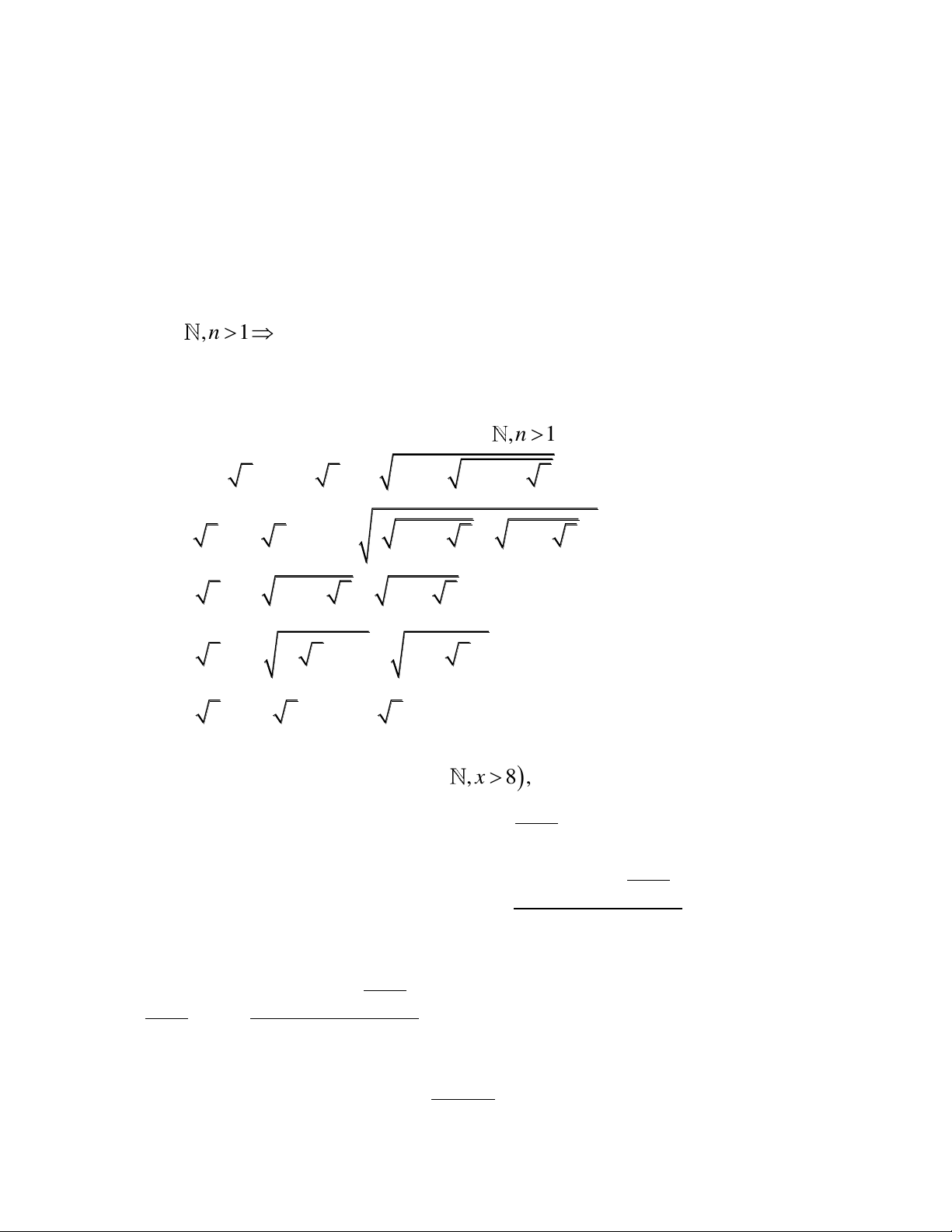
Câu 1.
a) Chứng minh rằng số có dạng
6 4 3 2
22A n n n n
không phải là số chính
phương, trong đó
,1nn
b) Rút gọn biểu thức:
13 4 3 7 4 3 8 20 2 43 24 3B
Câu 2.
a) Một người mang trứng ra chợ bán. Tổng số trứng bán ra được tính như sau:
Ngày thứ nhất bán được 8 trứng và
1
8
số trứng còn lại. Ngày thứ hai bán
được 16 trứng và
1
8
số trứng còn lại. Ngày thứ ba bán được 24 trứng và
1
8
số
trứng còn lại. Cứ như vậy cho đến ngày cuối cùng thì bán hết trứng. Biết số
trứng bán được mỗi ngày đều bằng nhau. Hỏi tổng số trứng người đó bán
được là bao nhiêu và bán hết trong mấy giờ
b) Giải hệ phương trình:
7 2 5
22
x y x y
x y x y
Câu 3.
a) Cho phương trình
2
2018 2019 2020 0x m x
(m là tham số). Tìm
để phương trình có hai nghiệm
12
,xx
thỏa mãn:
22
1 1 1 2
2019 2019x x x x
b) Giải phương trình:
23
2 2 5 1xx
Câu 4. Cho
ABC
không cân, biết
ABC
ngoại tiếp đường tròn (I). Gọi
,,D E F
lần lượt là các tiếp điểm của
,,BC CA AB
với đường tròn (I). Gọi M là giao điểm
của đường thẳng
EF
và đường thẳng BC, biết
AD
cắt đường tròn (I) tại điểm N
.ND
Gọi K là giao điểm của
,AI EF
a) Chứng minh rằng
..AK AI AN AD
và các điểm
, , ,I D N K
cùng thuộc đường
một đường tròn
b) Chứng minh
MN
là tiếp tuyến của đường tròn (I).
Câu 5. Cho đường tròn
;OR
và hai điểm
,BC
cố định sao cho
0
120 .BOC
Điểm
A di động trên cung lớn BC sao cho
ABC
nhọn. Gọi E là điểm đối xứng với B
qua AC và F là điểm đối xứng với C qua AB. Các đường tròn ngoại tiếp
,ABE ACF
cắt nhau tại
.K K A
Gọi H là giao điểm của
,BE CF
a) Chứng minh KA là phân giác trong góc BKC và tứ giác
BHCK
nội tiếp
b) Xác định vị trí điểm
A
để diện tích tứ giác
BHCK
lớn nhất, tính diện tích lớn
nhất của tứ giác
BHCK
theo
.R
ĐÁP ÁN
Câu 1. a) Ta có:
6 4 3 2
22
2 3 2
2
22
22
1 1 2 1
1 1 1
1 2 2
A n n n n
n n n n n
n n n n
n n n n




Với
22
2
, 1 2 2 1 1 1n n n n n n
Và
2 2 2
2 2 2 1n n n n n
Vậy
222
1 2 2n n n n
nên
222nn
không là số chính phương.
Do đó A không là số chính phương với
,1nn
2
22
) 13 4 3 7 4 3 8 20 2 43 24 3
91 52 3 28 3 48 8 13 4 3 7 4 3
43 24 3 8 13 4 3 7 4 3
43 24 3 8 2 3 1 2 3
43 24 3 8 2 3 1 2 3 35
bB



Câu 2.
a) Gọi
x
là số trứng bán được
, 8 ,xx
thì:
Số trứng bán được trong ngày thứ nhất là:
8
88
x
Số trứng bán được trong ngày thứ hai là:
8
16 8 8
16 8
x
x



Theo bài ta có phương trình:
8
16 8
88
8 16 392
88
x
x
xx



Vậy tổng số trứng bán được là 392 trứng
Số trứng bán được mỗi ngày là :
392 8
8 56
8

Số ngày là:
392:56 7
(ngày)
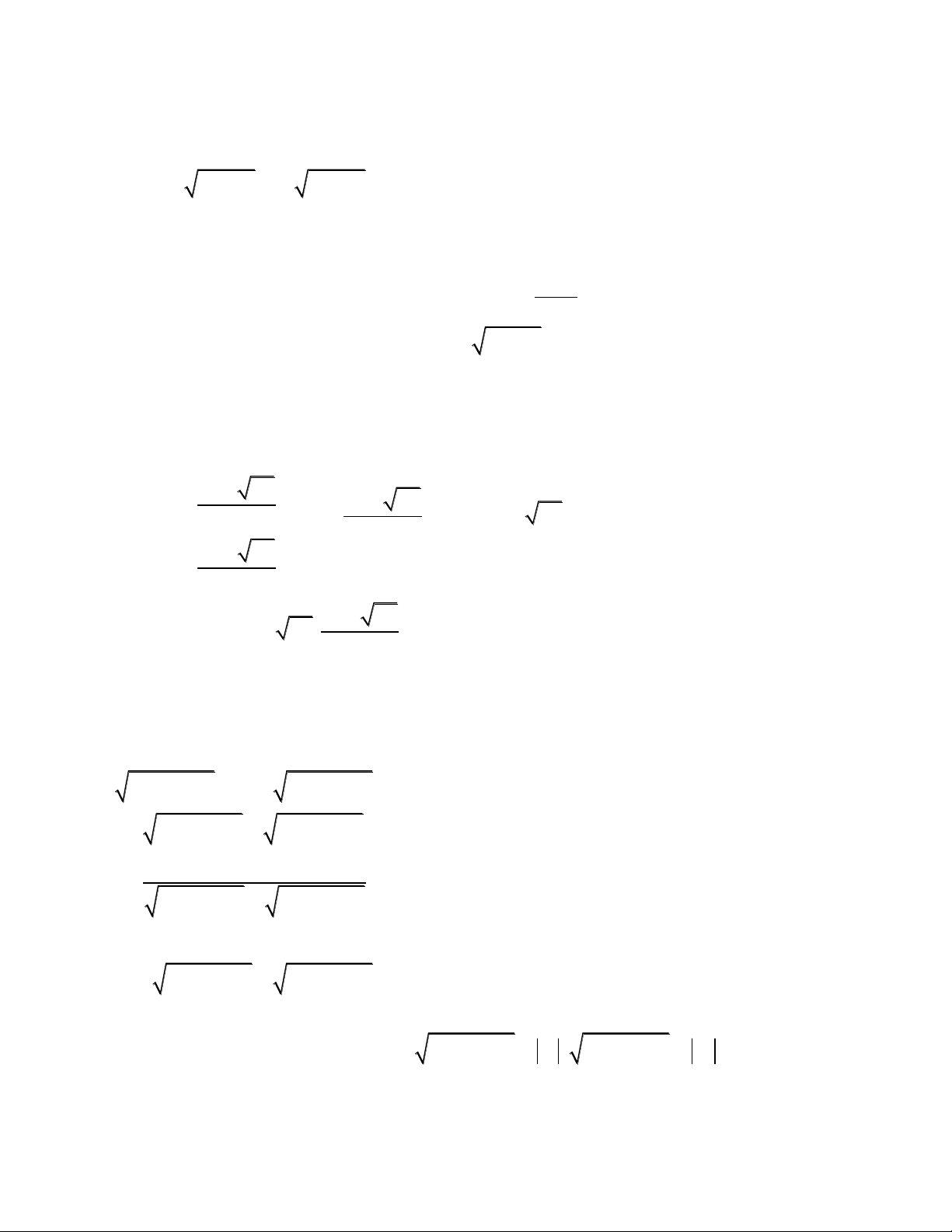
b) Điều kiện:
70
*
20
xy
xy


Đặt
7 , 2 , 0u x y v x y u v
Hệ phương trình đã cho trở thành:
5 (1)
2 (2)
uv
v x y

Ta thấy
22
5u v x
, kết hợp với (1) suy ra:
5
2
x
v
, thay vào (2) ta được:
2 1 (3)xy

. Thay
3
vào (2) ta có:
5 2 3yy
22
33
11 11 0
5 2 3
3
11 77 11 77 10 77( )
22
11 77
2
yy
yy
yy
y
yy x tm
y


Vậy
11 77
, 10 77; 2
xy 



Câu 3.
a) Do
0ac
nên phương trình luôn có hai nghiệm phân biệt với mọi giá trị của
m
Ta có:
22
1 1 2 2
22
1 2 2 1
22
12 21
22
12
12
22
1 2 1 2
2019 2019
2019 2019
2019 2019
0
2019 2019
x x x x
x x x x
xx xx
xx
xx
x x x x

*Trường hợp 1:
12
0 2019 0 2019x x m m
*Trường hợp 2: Không xảy ra do:
22
1 1 2 2
2019 ; 2019x x x x
Vậy
2019m
b)ĐK:
310x