Tr−êng THPT chuyªn ha long
§Ò thi thö ®¹i häc lÇn thø nhÊt
Năm học 2009- 2010
Môn Thi : Toán - Khối B
Thời gian làm bài: 180 phút
A. Phần chung dành cho tất cả các thí sinh ( 7 ñiểm)
Câu I: ( 2 ñiểm) Cho hàm số 1
12
+
+
=
x
x
y
1 Khảo sát và vẽ ñồ thị hàm số.
2 T×m trªn ®å thÞ nh÷ng ®iÓm cã tæng kho¶ng c¸ch ®Õn hai tiÖm cËn nhá nhÊt
Câu II ( 2 ñiểm)
1 Giải phương trình lượng giác : )2cos2(sin2cottan xxxx +=+
2 Giải ph−¬ng tr×nh: 1
3
)29
(log2=
−
−
x
x
Câu III ( 1 ñiểm)
Tính giới hạn sau : 2
0)11(
cos1
lim x
x
x−−
−
→
Câu IV: ( 1 ñiểm)
Cho ®−êng trßn t©m O b¸n kÝnh R. H×nh chãp SABCD cã SA cè ®Þnh vµ vu«ng gãc víi mÆt ph¼ng ®¸y,
SA = h; ®¸y ABCD lµ tø gi¸c thay ®æi nh−ng lu«n néi tiÕp trong ®−êng trßn ®A cho vµ cã hai ®−êng chÐo AC vµ
BD vu«ng gãc víi nhau
1 TÝnh b¸n kÝnh mÆt cÇu ngo¹i tiÕp h×nh chãp SABCD
2 X¸c ®Þnh h×nh d¹ng cña tø gi¸c ABCD ®Ó thÓ tÝch h×nh chãp ®¹t gi¸ trÞ lín nhÊt
Câu V ( 1 ñiểm)
T×m gi¸ trÞ lín nhÊt, gi¸ trÞ nhá nhÊt cña hµm sè: 3)
4
sin(2sin +++=
π
xxy trªn
−2
;
2
ππ
B.Phần riêng ( 3ñiểm)
Thí sinh chỉ ñược làm một trong hai phần ( Phần 1 hoặc phần 2)
Phần1.Theo chương trình chuẩn
Câu VI.a ( 2 ñiểm). Trong mÆt ph¼ng Oxy:
1 Cho h×nh thoi ABCD cã A(1;3), B(4; -1), AD song song víi trôc Ox vµ xD < 0. T×m to¹ ®é ®Ønh C, D
2 Cho ®−êmg trßn (C) cã ph−¬ng tr×nh 02042
22 =−+−+ yxyx vµ ®iÓm A(4;5). ViÕt ph−¬ng tr×nh
®−êng th¼ng ®i qua A vµ c¾t ®−êng trßn (C) t¹i hai ®iÓm E, F sao cho EF cã ®é dµi b»ng 8
Câu VII.a ( 1 ñiểm)
Khai triÓn 15
15
2
21
532 ....)1( xaxaxaaxxx o++++=+++
TÝnh : HÖ sè a10
Phần2.Theo chương trình nâng cao
Câu VI.b (2 ñiểm)
1 Trong mÆt ph¼ng Oxy cho tam gi¸c ABC cã ®Ønh A n»m trªn ®−êng th¼ng ∆: 01432 =+− yx , c¹nh
BC song song víi ∆, ®−êng cao CH cã ph−¬ng tr×nh 012 =−− yx . BiÕt trung ®iÓm cña c¹nh AB lµ M(-3; 0).
X¸c ®Þnh to¹ ®é c¸c ®Ønh A, B, C.
2 Cho ®−êmg trßn (C) cã ph−¬ng tr×nh 0442
22 =−−−+ yxyx vµ ®iÓm A(2;1).
+) Chøng tá r»ng ®iÓm A n»m trong ®−êng trßn (C).
+) ViÕt ph−¬ng tr×nh ®−êng th¼ng ®i qua A vµ c¾t ®−êng trßn (C) t¹i hai ®iÓm E, F sao cho A lµ trung
®iÓm cña EF
Câu VII.b ( 1ñiểm)
Cho 8 quc©n cã träng l−îng lÇn l−ît lµ 1kg, 2kg, 3kg, 4kg, 5kg, 6kg, 7kg, 8kg. LÊy ngÉu nhiªn ba qu¶
c©n trong sè ®ã. TÝnh x¸c suÊt ®Ó tæng träng l−îng 3 qu¶ c©n lÊy ®−îc kh«ng v−ît qu¸ 9kg.
TRƯỜNG THCS & THPT NGUYỄN KHUYẾN ĐỀ THỬ SỨC ĐẠI HỌC 2010
LỚP 12D1 Môn thi: Toán
Thời gian: 180 phút
ĐỀ
SỐ
030
http://www.VNMATH.com
http://www.VNMATH.com
30
http://www.VNMATH.com
ðáp án To¸n – Khèi B- Thi thử ñại học lần 1 năm học 2009-2010
Câu
Lời giải ðiể
m
Câu
I.1
( 1
ñiểm)
C©u
I.2
(1®iÓ
m)
TXð : D= R\{-1}
1,0
)1(
1
'2−≠∀>
+
=x
x
y
Hµm sè ®ång biÕn trªn (-∞;-1) vµ (-1;+
Kh«ng cã ®iÓm cùc ®¹i, cùc tiÓu
…………………………………………………………………………………………
Giíi h¹n vµ tiÖm cËn 2lim =
±∞→
y
x; tiÖm cËn ngang : y = 2
−∞=+∞= +−
−→−→
yy
xx
11
lim;lim ; tiÖm cËn ®øng x = -1
…………………………………………………………………………………………
BBT
…………………………………………………………………………………………
§å thÞ:
LÊy M(x0,y0) )(C
∈
)
1
1
2;(
0
0
+
−⇒
x
xM .
…………………………………………………………………………………………
Tæng kho¶ng c¸ch tõ M ®Õn hai ®−êng tiÖm cËn lµ 2|
1
1
||1| ≥
+
++=
xh
…………………………………………………………………………………………
−=
=
⇔±=+⇔=
+
=+⇔= 2
0
111|
1
1
||1|2 x
x
x
x
xh
…………………………………………………………………………………………
VËy cã hai ®iÓm trªn ®å thÞ cÇn t×m lµ M(0;1); M’(-2;3)
x
y’
y
0,25
0,25
0,25
0,25
-----
0,25
0,25
0,25
0,25
Câu
II.1
(1
ñiểm)
ðiều kiện: sinxcosx 0
≠
…………………………………………………………………………………………
pt )2cos2(sin2sin1)2cos2(sin2
cos
sin
1xxxxx
+=⇔+=⇔
………………………………………………………………………………………….
=
=
⇔=⇔=−⇔ xx
x
xxxxxx 2sin2cos
02cos
2cos2sin2cos2cos2sin2sin1
22
…………………………………………………………………………………………
Zk
kx
kx
x
x∈
+=
+=
⇔
=
=
⇔,
28
2
4
12tan
02cos
ππ
ππ
0,25
0,25
0,25
0,25
Đ
Ề
S
Ố
030
http://tranthanhhai.tk
http://www.VNMATH.com
http://www.VNMATH.com
118
http://www.VNMATH.com
C©u
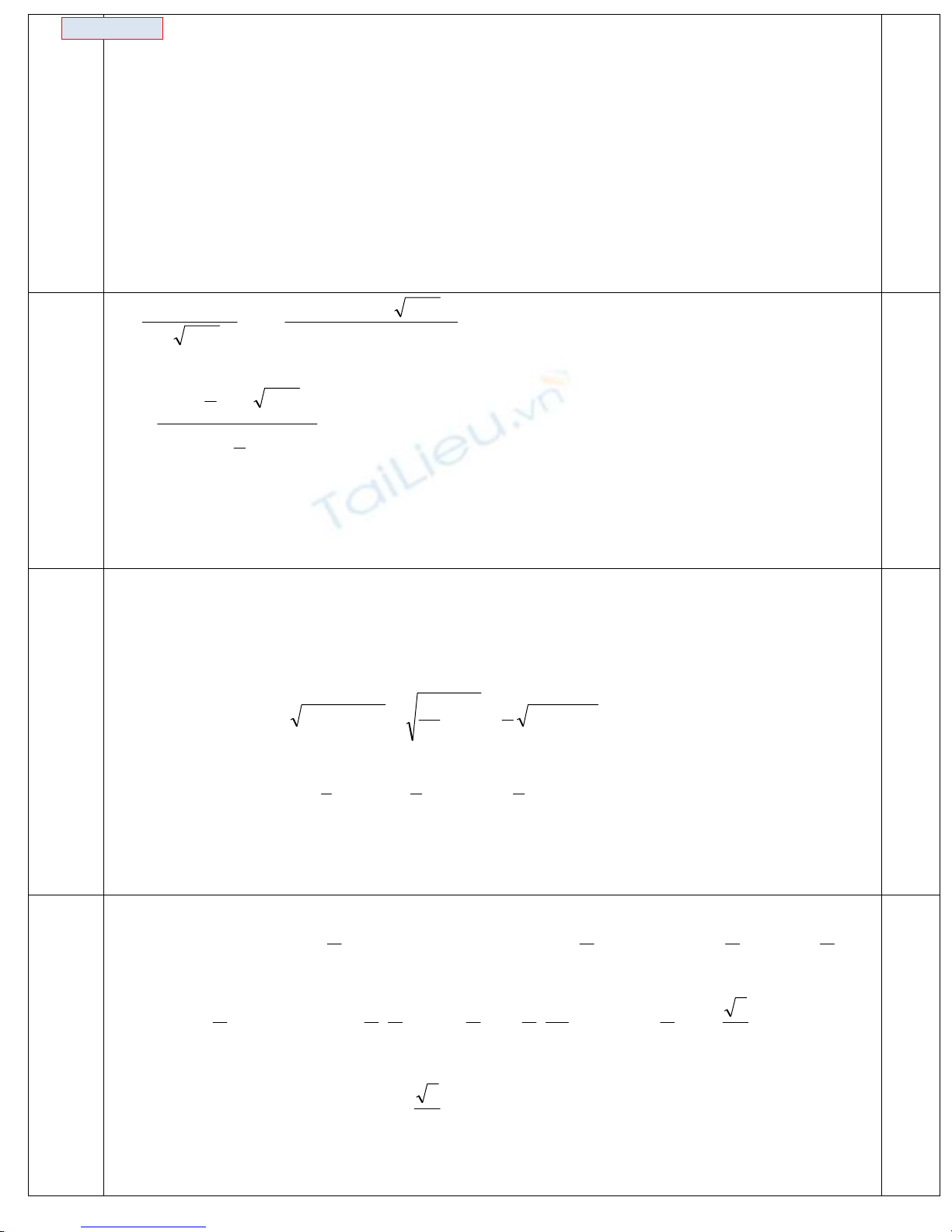
II.2
(1®iÓ
m)
§k:
>−
≠
029
3
x
x
…………………………………………………………………………………………
pt xxx x
−
=−⇔−=−⇔
3
2
2293)29(log
…………………………………………………………………………………………
Pt ®−a vÒ
=
=
⇔=
+− 82
12
082.9)2( 2
x
x
xx
…………………………………………………………………………………………
=
=
⇔)(3
0
loaix
x VËy pt cã mét nghiÖm x = 0
0,25
0,25
0,25
0,25
Câu
III
1
ñiÓm
2
2
0
2
0
)11).(cos1(
lim
)11(
cos1
lim x
xx
x
x
xx
−+−
=
−−
−
→→
…………………………………………………………………………………..
2
22
0)
2
.(4
)11.(
2
sin2
lim x
x
x
x
−+
=
→
………………………………………………………………………………………..
= 2
0,25
0,5
0,25
Câu
IV
1
ñiểm
Gäi I lµ t©m mÆt cÇu ngo¹i tiÕp h×nh chãp ta cã I n»m trªn ®−êng th¼ng Ot vu«ng gãc
víi mp(ABCD) t¹i O. V× SA vu«ng gãc víi (ABCD) nªn Ot//SA
…………………………………………………………………………………………
Trong mp(SA,Ot), giao cña ®−êng trung trùc ®o¹n SA vµ Ot lµ t©m I cña mÆt cÇu
…………………………………………………………………………………………
TÝnh ®−îc R = IA 222
2
22 4
2
1
4RhR
h
OAOI +=+=+=
…………………………………………………………………………………………
ThÓ tÝch h×nh chãp RRhBDAChhSV ABCD 2.2.
6
1
..
6
1
.
3
1≤==
V ®¹t gi¸ trÞ lín nhÊt khi AC = BD = 2R. VËy khi tø gi¸c ABCD lµ h×nh vu«ng th× h×nh
chãp ®¹t gi¸ trÞ lín nhÊt
0,25
0,25
0,25
0,25
C©u V
1®iÓm
Ta cã
2)
4
sin()
4
(sin22)
4
sin()cos(sin2)
4
sin(cossin21 22 ++++=++++=++++=
π
π
π
π
xxxxxxxxy
…………………………………………………………………………………………
§Æt tx =+ )
4
sin(
π
. Do
−∈+⇒
−∈+⇒
−∈ 1;
2
2
)
4
sin(
4
3
;
442
;
2
ππππππ
xxx
…………………………………………………………………………………………
XÐt hµm sè 22 2++= tty trªn
−1;
2
2, ta cã b¶ng biÕn thiªn
0,25
0,25
0,25
Đ
Ề
S
Ố
030
http://tranthanhhai.tk
http://www.VNMATH.com
http://www.VNMATH.com
119
http://www.VNMATH.com
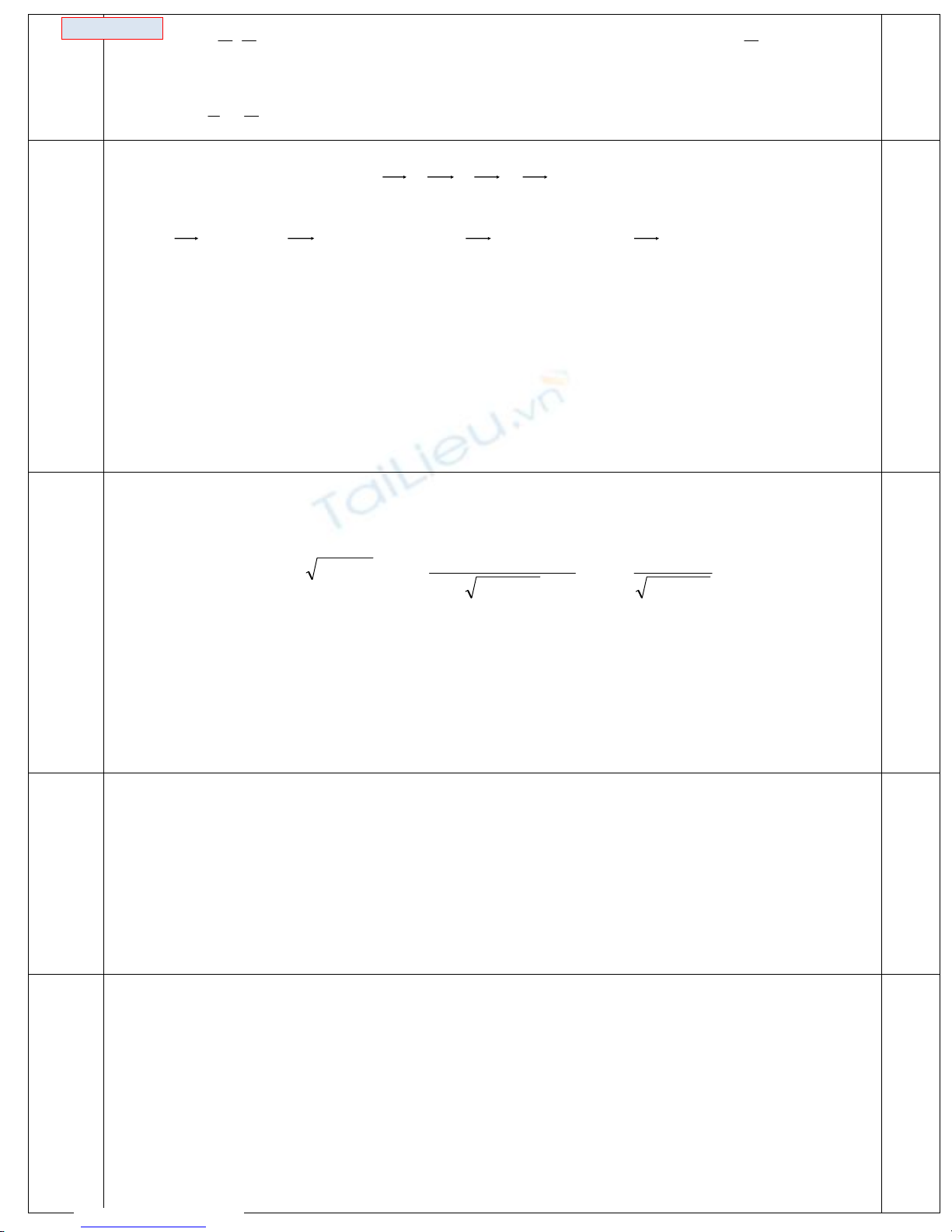
VËy trªn
−2
;
2
ππ
hµm sè ®A cho ®¹t gi¸ trÞ lín nhÊt lµ: maxy=1 khi
4
π
=x
®¹t gi¸ trÞ nhá nhÊt lµ: miny=2 khi
4
)
4
1
arcsin(
π
−−=x
0,25
Câu
VIa. 1
1
ñiểm
V× BC//AD//Ox nªn C(xC;-1); D(xD;3)
Do ABCD lµ h×nh thoi nªn cã BDACDCAB ⊥= ;
…………………………………………………………………………………………
Ta cã )4;4(),4;1(),4;()4;3( −=−−=−−=−= DCDC xBDxACxxDCAB
Ta cã hÖ pt
−=
−
=
=
=
⇔
=−−
+=
⇔
=−−−
=−
4
1
6
9
0242
3
016)4).(1(
3
2
D
C
D
C
DD
DC
DC
D
C
x
x
x
x
xx
x
x
xx
xx
…………………………………………………………………………………………
V× xD<0 nªn C(-1;-1); D(-4;3)
0,25
0,25
0,25
0,25
Câu
VI.a.2
1
ñiểm
§−êng trßn (C) cã t©m I(1;-2), b¸n kÝnh R=5
§−êng th¼ng (d) qua A(4;5) cã ph−¬ng tr×nh )0(,0)5()4( 22 ≠+=−+− BAyBxA
…………………………………………………………………………………………
Do EF = 8 3
|73|
3
|542|
345),( 2222
22 =
+
+
⇔=
+
−
−
−
⇒=−=⇒
BA
BA
BA
BABA
dId
…………………………………………………………………………………………
BiÕn ®æi ®−a vÒ
=+
=
⇔=+ 02021
0
04042 2
BA
B
BAB
…………………………………………………………………………………………
+) Víi B=0 cã pt (d) : x = 4
+) Víi 21A+20B = 0 cã ph−¬ng tr×nh (d): 20x-21y+25=0
0,25
0,25
0,25
0,25
Câu
VII a.
1
ñiểm
Ta cã 525532 )1()1()1()( xxxxxxf ++=+++=
…………………………………………………………………………………………
105
5
84
5
63
5
42
5
21
5
0
5
52
55
5
44
5
33
5
22
5
1
5
0
5
5
)1(
)1(
xCxCxCxCxCCx
xCxCxCxCxCCx
+++++=+
+++++=+
…………………………………………………………………………………………
Suy ra 10150501
3
5
4
5
4
5
2
5
5
5
0
510 =++=++= CCCCCCa
0,25
0,25
0,5
Câu
VI.b.1
1ñiểm
C¹nh AB qua M vµ vu«ng gãc víi ®−êng cao CH nªn cã pt: 620)3(2
+
+
⇔
=
+
+
yxyx
To¹ ®é ®iÓm A lµ nghiÖm cña hÖ
=
−=
⇔
=++
=+−
2
4
062
01432
y
x
yx
yx VËy A(-4;2)
…………………………………………………………………………………………
M lµ trung ®iÓm AB nªn tÝnh ®−îc to¹ ®é ®Ønh B(-2;-2)
…………………………………………………………………………………………
C¹nh BC //∆ vµ qua B nªn pt BC lµ 2(x+2) – 3(y+2) = 0
To¹ ®é cña C lµ nghiÖm cña hÖ
=
=
⇔
=−
−
=−−
0
1
0232
012
y
x
yx
yx VËy to¹ ®é ®Ønh C(1;0)
0,5
0,25
0,25
Đ
Ề
S
Ố
030
http://tranthanhhai.tk
http://www.VNMATH.com
http://www.VNMATH.com
120
http://www.VNMATH.com
C©u
VIb.2
1®iÓm
§−êng trßn (C) cã t©m I(1;2), b¸n kÝnh R= 3
…………………………………………………………………………………………
Ta cã RIA <=+= 211 . VËy A n»m trong ®−êng trßn
…………………………………………………………………………………………
(d) c¾t ®−êng trßn t¹i hai ®iÓm E,F mµ A lµ trung ®iÓm nªn IA
⊥
EF hay (d) nhËn
)1;1( −IA lµm vect¬ ph¸p tuyÕn
…………………………………………………………………………………………
Ph−¬ng tr×nh ®−êng th¼ng cÇn t×m lµ: x – y – 1 = 0
0,25
0,25
0,25
0,25
C©u
VIIb
1®iÓm
Sè c¸ch lÊy ngÉu nhiªn ba qu¶ c©n lµ 56)(56
3
8=Ω⇒=nC
…………………………………………………………………………………………
C¸c c¸ch lÊy ra ba qu¶ c©n cã träng l−îng kh«ng v−ît qu¸ 9 kg lµ (1;2;3), (1;2;4),
(1;2;5), (1;2;6), (1;3;4), (1;3;5), (2,3,4), cã 7 c¸ch
…………………………………………………………………………………………
Gäi A lµ biÕn cè lÊy ®−îc ba qu¶ c©n cã träng l−îng kh«ng v−ît qu¸ 9kg, ta cã n(A)=7
VËy 125,0
56
7
)(
)(
)( ==
Ω
=n
An
AP
0,25
0,25
0,5
Trªn ®©y lµ tãm t¾t c¸ch gi¶i, cÇn l−u ý lËp luËn cña häc sinh trong qu¸ tr×nh gi¶i bµi. NÕu häc
sinh lµm theo c¸c c¸ch kh¸c nhau tæ chÊm th¶o luËn ®Ó chia ®iÓm thèng nhÊt. §iÓm toµn bµi
kh«ng lµm trßn
Đ
Ề
S
Ố
030
http://tranthanhhai.tk
http://www.VNMATH.com
http://www.VNMATH.com
121
http://www.VNMATH.com