Chương 1Chương 1
18/08/2006
Chương 2: Mô hình quá trình
-phần I
Đ
Đi
iề
ều
ukhi
khiể
ển
nqu
quá
átr
trì
ình
nh
2
Chương 2: Mô hình quá trình © 2006 - HMS
2.1 Giớithiệu chung
2.2 Các dạng mô hình toán học
2.3 Mô hình hóa lý thuyết
2.4 Mô hình hóa thựcnghiệm
Nộidung chương 2
3
Chương 2: Mô hình quá trình © 2006 - HMS
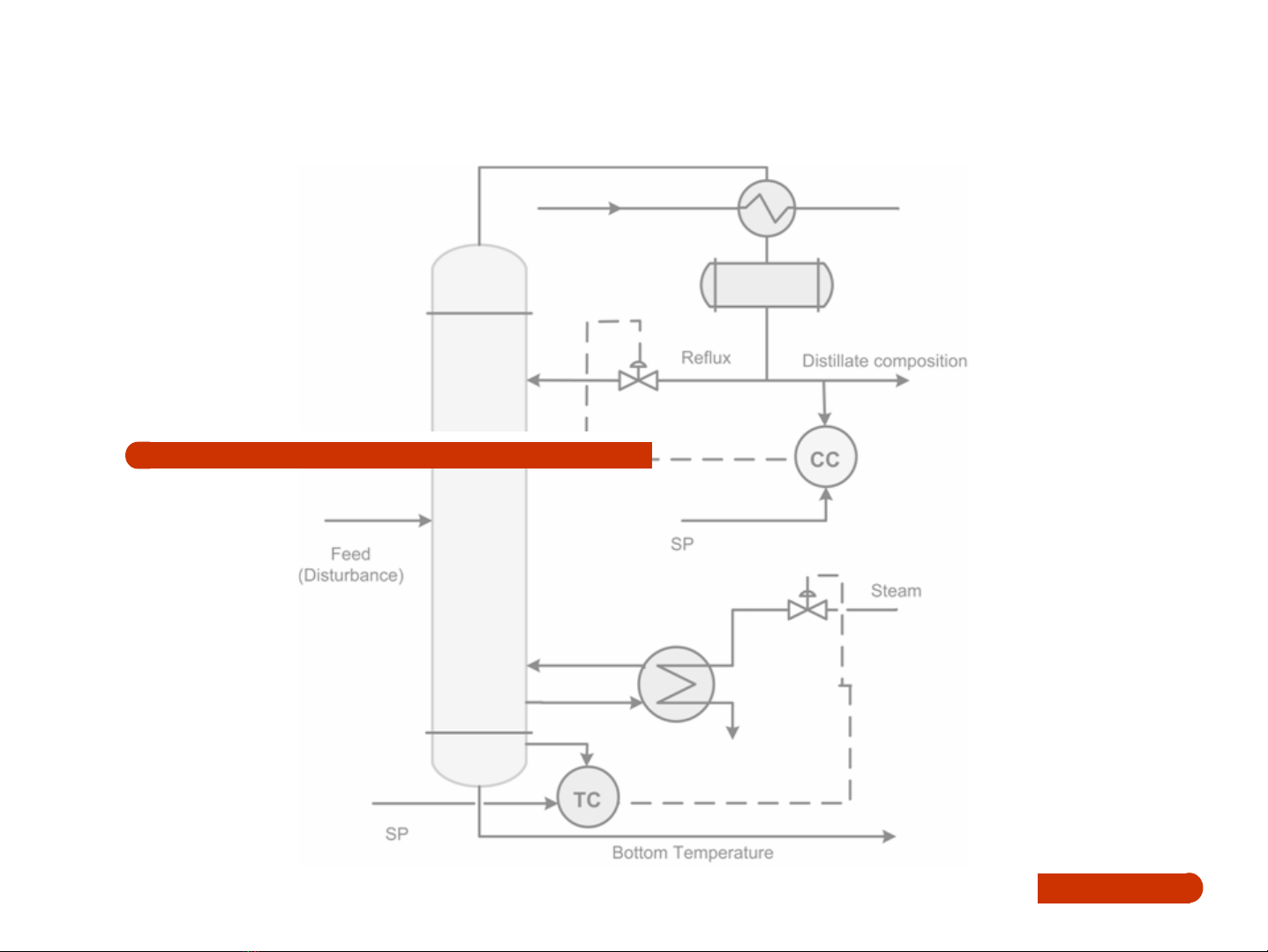
2.1 Giới thiệu chung
Mô hình là mộthìnhthứcmôtảkhoa họcvàcô₫ọng các khía
cạnh thiếtyếucủamộthệthống thực, có thểcó sẵnhoặccần
phảixâydựng.
Một mô hình phảnánhhệthống thựctừmột góc nhìn nào
đóphụcvụhữu ích cho mụcđích sửdụng.
Phân loại mô hình:
—Môhìnhđồ họa: Sơđồkhối, lưuđồ P&ID, lưuđồ thuậttoán
— Mô hình toán học: ODE, Hàm truyền, mô hình trạng thái
— Mô hình máy tính: Chương trình phầnmềm
—Môhìnhsuyluận: Cơsởtri thức, luật
Trong nội dung chương 2 ta quan tâm tớixây dựng mô hình
toán học cho các quá trình công nghệ.
4
Chương 2: Mô hình quá trình © 2006 - HMS
Mục₫ích sửdụng mô hình
1. Hiểurõ hơn vềquá trình
2. Thiếtkếcấu trúc/sách lượcđiềukhiểnvàlựa
chọnkiểubộđiềukhiển
3. Tính toán và chỉnh định các tham sốcủabộđiều
khiển
4. Xác định điểmlàmviệctốiưuchohệthống
5. Mô phỏng, đào tạongườivậnhành
5
Chương 2: Mô hình quá trình © 2006 - HMS
Thếnào là mộtmôhìnhtốt
Chấtlượng mô hình thểhiệnqua:
— Tính trung thựccủa mô hình: Mứcđộ chi tiếtvàmứcđộ
chính xác của mô hình
—Giátrịsửdụng (phù hợptheomụcđích sửdụng)
—Mứcđộ đơngiảncủa mô hình
“Không có mô hình nào chính xác, nhưng mộtsốmô
hình có ích”.
Mộtmôhìnhtốtcầnđơngiảnnhưng thâu tóm
đượccácđặctínhthiếtyếucầnquantâmcủathế
giớithực trong mộtngữcảnh sửdụng.