Nguyễn Trọng Nghĩa. Tạp chí Khoa học Đại học Mở Thành phố Hồ Chí Minh, 61(4), 21-32 21
DỰ ĐOÁN SỰ TIÊU TÁN ÁP LỰC NƯỚC LỖ RỖNG
CỦA BÀI TOÁN BẤC THẤM (BÀI TOÁN 1D)
NGUYỄN TRỌNG NGHĨA
Trường Đại học Mở Thành phố Hồ Chí Minh - nghia.nt@ou.edu.vn
(Ngày nhận: 26/03/2018; Ngày nhận lại: 17/04/2018; Ngày duyệt đăng: 10/07/2018)
TÓM TẮT
Bấc thấm (PVD) được sử dụng khá rộng rãi trong việc thúc đẩy nhanh quá trình cố kết trong đất yếu, qua đó
tăng cường tính chất của đất và giảm lún. Giải bài toán cố kết của bấc thấm được giải bằng nhiều phương pháp khác
nhau như: Phương pháp giải tích, Phương pháp sai phân hữu hạn và phương pháp phần tử hữu hạn. Trong đó,
phương pháp giải tích với kỹ thuật biến đổi Laplace đã làm cho bài toán giải tích trở nên mạnh hơn và có thể giải
được hầu hết các trường hợp chất tải theo thời gian. Bài báo này trình bày phương pháp sử dụng kỹ thuật biến đổi
Laplace để giải bài toán PVD xuyên một phần vào trong đất với giả sử đầu mũi là không thấm. Lời giải sử dụng biện
pháp tích hợp các bài toán cố kết phương đứng và ngang để có được phương pháp tính cố kết đơn giản theo 1D.
Cùng với giả sử đầu mũi là không thấm, bài toán đã giảm đi các biến trong quá trình tính toán và trở nên đơn giản
hơn rất nhiều. Lý thuyết tính toán được kiểm nghiệm lại với kết quả đo tại một đập thử nghiệm ở sân bay quốc tế
Thái Lan. Áp lực nước lỗ rỗng và độ lún từ kết quả tính toán lý thuyết là tương thích cao với kết quả đo đạc thực tế.
Từ khóa: Bấc thấm (PVD); Cố kết; Đất yếu; Kỹ thuật biến đổi Laplace; Phương pháp giải tích.
Predicting pore pressure estimation in vertical drains (1D problem)
ABSTRACT
Prefabricated vertical drain (PVD) has been widely utilized in facilitating the consolidation process of soft soil,
through that it will increase soil properties and reduce residual settlement. The consolidation problems with PVD
have been solved by many different approaches including, Analytical methods, finite difference methods, and finite
element methods. Among them, the analytical method with Laplace transform technique has stronger and capable of
solving cases of loading with time. This paper presents a solution with utilizing Laplace transform technique to deal
with the problem of partially penetrated PVDs with the impervious drain’s end. The solution has combined the
vertical and horizontal consolidation process into 1D consolidation. The assumption of impervious drain’s end has
reduced the variants and more simplifies the solution. To verify present solution, a test embankment in international
airport Thailand has been analyzed. The estimated pore pressure and settlement from present solution are excellent
agreement with the field data.
Keywords: Prefabricated vertical drain (PVD); Consolidation; Soft soil; Laplace transform technique;
Analytical method.
1. Giới thiệu
Bấc thấm được sử dụng rộng rãi vì đây là
biện pháp tiết kiệm cả thời gian lẫn chi phí
trong xử lý nền. Các biện pháp thi công với
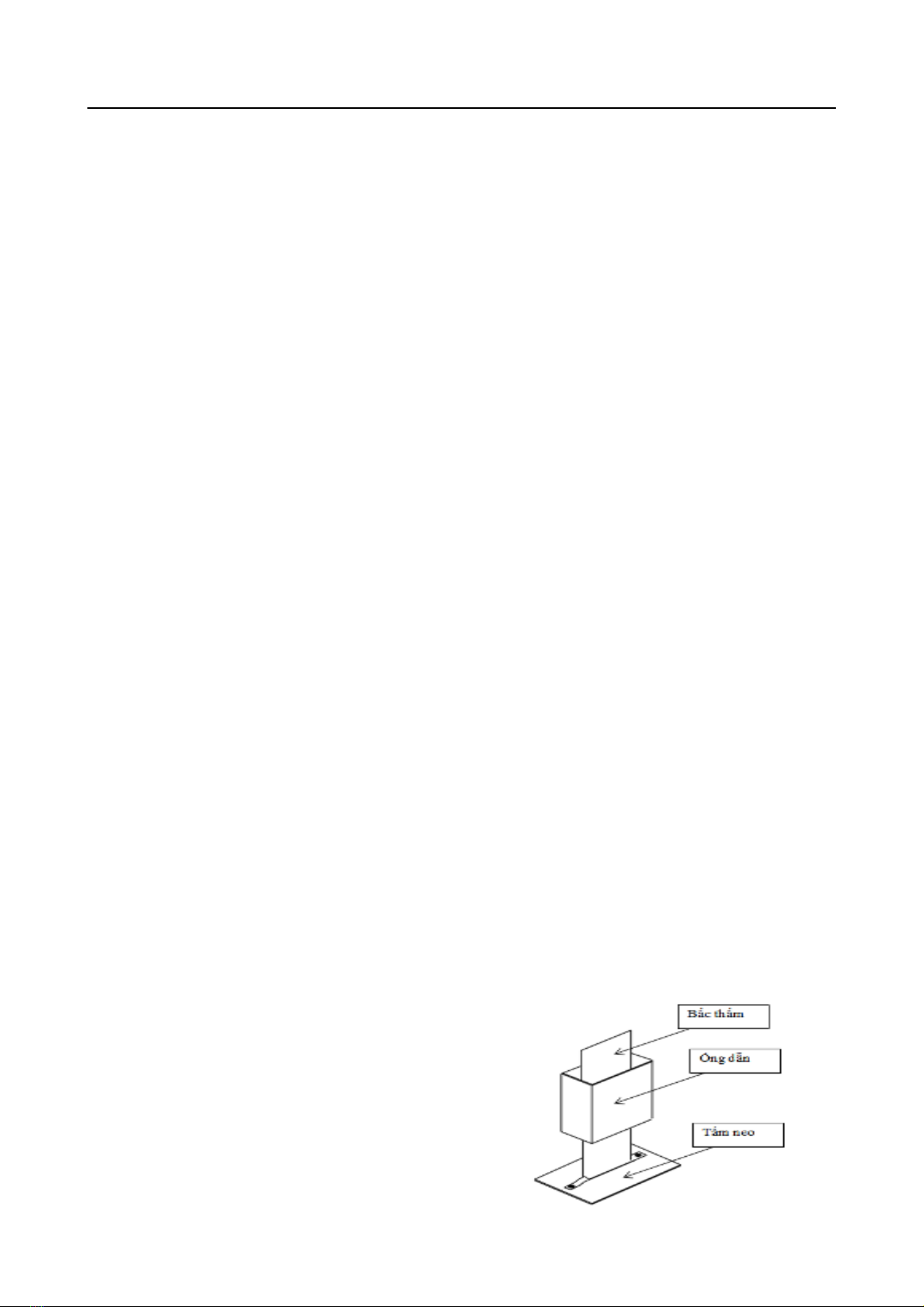
các đầu mũi neo khác nhau được mô tả theo
nghiên cứu của Bo và cộng sự (2015). Trong
đó, biện pháp thi công sử dụng đầu mũi neo
dạng tấm (Hình 1) được sử dụng khá rộng rãi.
Ðầu mũi neo này lại chặn không cho quá trình
thấm diễn ra từ bên dưới PVD từ đó bài toán
cố kết trong PVD phải xem biên tại mũi là
biên không thấm thì mới đúng với điều kiện
làm việc thực tế. Hầu hết các nghiên cứu trước
đây đều xem tại đầu mũi là biên thấm được.
Hình 1. Mô hình bấc thấm và tấm neo
22 Nguyễn Trọng Nghĩa. Tạp chí Khoa học Đại học Mở Thành phố Hồ Chí Minh, 61(4), 21-32
Bài toán cố kết bấc thấm đã được phân
tích từ nhiều phương pháp khác nhau như
phương pháp giải tích, phương pháp bán giải
tích, phương pháp sai phân hữu hạn, phương
pháp phần tử hữu hạn. Các phân tích bao gồm
Indraratna và cộng sự (2000, 2005 và 2008),
Chai và cộng sự (2001), Voottipruex và cộng
sự (2014), Lam và cộng sự (2015), Indraratna
và Rujikiatkamjorn (2008), Geng và cộng sự
(2011), Tang và Onitsuka (1998 và 2001),
Zeng and Xie (13) hoặc Ong và cộng sự
(2012). Các nghiên cứu này xem đầu biên trên
của bấc thấm là thấm được trong khi chỉ có
nghiên cứu gần đây của Nghia và cộng sự
(2018) là kể đến vấn đề trên vào bài toán giải
tích. Tuy nhiên, lời giải từ phương pháp giải
tích có nhiều giới hạn vì chỉ áp dụng trong
điều kiện biên đơn giản và trường hợp tải đơn
giản như biên thấm hoặc tải tức thời. Ðiều này
làm giảm đi tính ứng dụng. Do đó, bài báo
này khắc phục yếu điểm của phương pháp giải
tích bằng cách kết hợp biến đổi Laplace cho
bấc thấm 1 phần trong đất để có thể giải được
bài toán gia tải theo thời gian. Một đập thí
nghiệm được phân tích lại để chứng tỏ khả
năng áp dụng của phương pháp này.
2. Mô hình cơ bản
Mô hình tổng quát cho bài toán bấc thấm
xuyên một phần được cho trong Hình 2. Có
hai trường hợp với điều kiện biên thấm khác
nhau là: thấm ở mặt và không thấm ở đáy
(PTIB); thấm ở mặt và thấm ở đáy (PTPB).
Ðầu mũi được xem như không thấm. Thông
thường địa chất dưới đầu mũi bấc thấm có thể
khác so với địa chất bên phía trên đầu mũi bấc
thấm vì bấc thấm thường được cắm xuống hết
phần đất yếu cho nên địa chất được phân thành
hai lớp như Hình 2. Một số ký hiệu được viết
tắt trong bài báo này như sau:
H
= Toàn bộ
chiều dày đất;
1
h
= chiều dài của PVD;
2
h
=
chiều dài phần đất không gia cường bằng
PVD;
w
r
= bán kính bấc;
s
r
= bán kính vùng
xáo động;
e
r
= bán kính tương đương;
h
k
= hệ
số thấm theo phương ngang của đất không bị
xáo động;
1v
k
= hệ số thấm đứng của đất có
PVD;
1v
m
= hệ số nén thể tích của đất chứa
PVD;
s
k
= hệ số thấm phương ngang của vùng
xáo động;
w
k
= hệ số thấm trong bấc;
2v
k
= hệ
số thấm trong đất không có PVD;
2v
m
= hệ số
nén thể tích của đất bên dưới PVD.
Hình 2. Mô hình phân tích bài toán PVD
Nguyễn Trọng Nghĩa. Tạp chí Khoa học Đại học Mở Thành phố Hồ Chí Minh, 61(4), 21-32 23
Phương trình căn bản được Tang và Onitsuka (1998 và 2001) xây dựng dựa trên sự kết hợp
quá trình thấm đứng và thấm ngang.
Ðối với khu vực có chứa PVD,
Phương trình chủ đạo cho áp lực nước lỗ rỗng tiêu
tán là:
Khu vực xáo động,
ws
r r r
2
1 1 1 1 11
22
11
1 ( )
s s s v
v w v w
k u u k u u t
m r r m t t
rz







(1)
Khu vực không bị xáo động,
se
r r r
2
1 1 1 1 11
22
11
1 ( )
h n n v
v w v w
k u u k u u t
m r r m t t
rz







(2)
Ðối với khu vực không có,
1
h z H
, Phương trình chủ đạo là:
2
222
2
2
()
v
vw
ku u t
m t t
z


(3)
trong đó
r
= trục xoay;
z
= trục đứng;
t
= thời gian;
w
= dung trọng nước;
1( , , )
s
u r z t
áp lực
nước lỗ rỗng tại khu vực xáo động;
1( , , )
n
u r z t
= Áp lực nước lỗ rỗng tại khu vực không bị xáo
động;
1( , )u z t
= Áp lực nước lỗ rỗng trung bình trong đất khu vực có PVD; và
2( , )u z t
= Áp lực
nước lỗ rỗng trong đất không chứa PVD.
()t
tải trọng theo thời gian.
Áp lực nước lỗ rỗng trung bình được xác định bằng:
1 1 1
22
122
()
se
w
rr
sn
ew
r rs
u ru dr ru dr
rr








(4)
Ðiều kiện biên và điều kiện liên tục như sau:
211
2
2
w
w s s
ww rr
u k u
r k r
z


 

(5)
10
e
n
rr
u
r
(6)
1ww
sw
r r r r
uu

(7)
11
ss
sn
r r r r
uu

(8)
11
11
ss
sn
sh
r r r r
uu
kk
rr



(9)
00
wz
u
(Thấm trên mặt trong bấc) (10)
100
z
u
(Thấm trên mặt trong đất) (11)
20
zH
u
z
(PTIB) (12)
24 Nguyễn Trọng Nghĩa. Tạp chí Khoa học Đại học Mở Thành phố Hồ Chí Minh, 61(4), 21-32
20
zH
u
(PTPB ) (13)
Biên không thấm mới tại vị trí đầu của bấc
1
zh
dẫn đến điều kiện liên tục như sau:
1
0
w
zh
u
z
(đầu không thấm trong bấc) (14)
11
12
z h z h
uu

(áp lực nước lỗ rỗng bằng nhau) (15)
11
2 2 2
12
12
()
v e w v e
z h z h
uu
k r r k r
zz





(Ðiều kiện liên tục) (16)
3. Lời giải đề xuất
3.1. Tổng quát
Thay thế các điều kiện bên trên vào phương trình tổng quát (1) và (2) để phương trình chỉ
còn liên quan đến 1 biến
( , )
w
u z t
theo Tang và Onitsuka (1998, 2001).
4 3 2
1 1 1 2
4 2 2
( , ) ( , ) ( , ) ( , ) () 0
w w w w
vh
u z t u z t u z t u z t t
cc
tt
z z t z





(17)
Phương trình (17) được xem như phương trình thấm 1 phương. Mối quan hệ giữa áp lực
nước lỗ rỗng trong bấc và áp lực nước lỗ rỗng trung bình cũng được phân tích (theo Tang và
Onitsuka 1998, 2001)
2
21
2
( , ) ( ( , ) ( , )) 0
ww
u z t u z t u z t
z
(18)
trong đó
11
11
11
2
22
11
12
2
, , , ,
2 2 1
1 ( 1) , ( 1) ,
v h s e
vh
v w v w w w
vh
w w e
e
k k r r
c c s n
m m r r
kk
nn
k F k r
rF




2 2 2
11
2 2 2 2 2
11
3 1 1
ln ln 1 1
41 1 4 1 4
hh
ss
kk
n n s s
Fs
s k k
n n n n n

 

 





Sử dụng kỹ thuật biến đổi Laplace cho phương trình (17) ta được.
42
1 1 1 2 2
42
( , ) ( , )
( ) ( ) ( , ) ( ) 0
ww
v h w o s
Lu z s Lu z s
c c s s Lu z s u s
zz


(19)
trong đó
( , )
w
Lu z s
là biến đổi Laplace của
( , )
w
u z t
( ,0)
wo
u z u
là giá trị áp lực nước lỗ rỗng ban đầu
()
ss
là biến đổi Laplace của
()t
t
Lời giải của phương trình (19) là
Nguyễn Trọng Nghĩa. Tạp chí Khoa học Đại học Mở Thành phố Hồ Chí Minh, 61(4), 21-32 25
1 1 2 2
1 2 3 4
()
( , ) os
a z a z a z a z
w
us
Lu z s X e X e X e X e s

(20)
trong đó
2
1 1 1 1 2 1
11
2
1 1 1 1 2 1
21
4
2
4
2
h h v
v
h h v
v
c s c s c s
ac
c s c s c s
ac
Biến đổi Laplace cho phương trình (18) ta có:
2
2 1 2
2
( , ) ( , ) ( , ) 0
ww
Lu z s Lu z s Lu z s
z

(21)
Trong đó
1( , )Lu z s
là biến đổi Laplace của
1( , )u z s
Thay thế phương trình (20) vào (21) để được giá trị biến đổi Laplace của áp lực nước lỗ
rỗng trung bình trong đất vùng có chứa PVD.
1 1 2 2
2 2 2 2
1 1 2 2
1 1 2 3 4
2 2 2 2
()
( , ) 1 1 1 1 0
os
a z a z a z a z us
a a a a
Lu z s X e X e X e X e s

(22)
Sử dụng kỹ thuật biến đổi Laplace cho phương trình (4) cho đất không chứa PVD.
22
22
2
( , ) ( , ) ( ( ))
v o s
Lu z s
c s Lu z s u s
z
(23)
Trong đó
2( , )Lu z s
là biến đổi Laplace của
2( , )u z t
Lời giải cho phương trình (23) là
11
2 5 6 ()
( , ) b z b z os
us
Lu z s X e X e s
(24)
Trong đó
12v
s
bc
3.2. Trường hợp (PTIB)
Sử dụng 6 điều kiện biên (10), (11), (12), (14), (15), và (16) vào 3 phương trình Laplace
(20), (22), và (24) để có được ma trận (6,6)
.T
PTIB PTIB
S X Q
(25)
Trong đó:
21 22 23 24
35 36
41 42 43 44
51 52 53 54 55 56
61 62 63 64 65 66
1 1 1 1 0 0
0 0
0 0 0 0
0 0
PTIB
S S S S
SS
SS S S S
S S S S S S
S S S S S S










1 2 3 4 5 6
X X X X X X X

( ) ( )
0 0 0 0
o s o s
PTIB
u s u s
Qss




