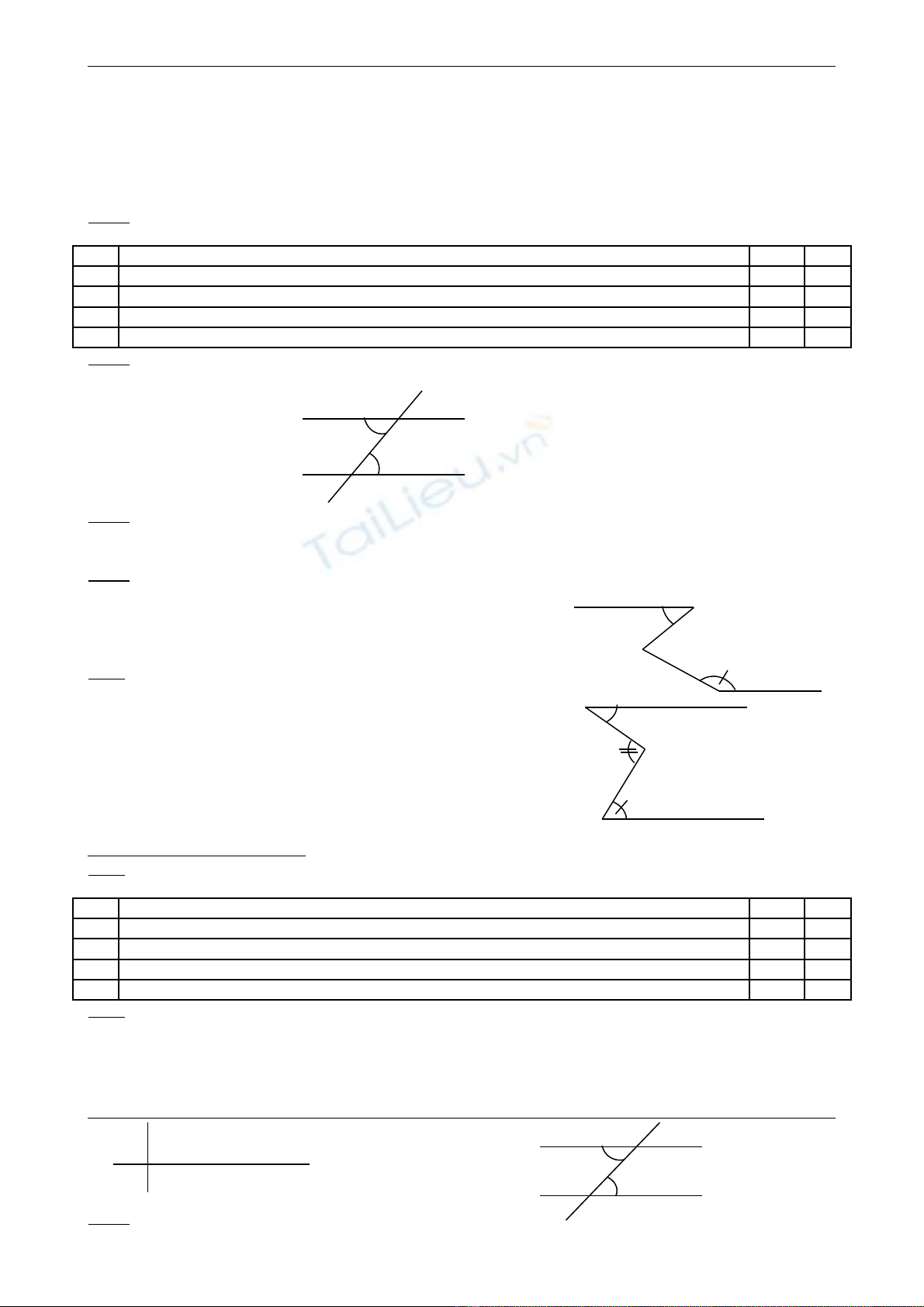
Cho hình vẽ bên. Biết At // By.
·
·
0 0
tAC 35 ;CBy 135= =
. Tính x?
TRÖÔØNG THCS LEÂ HOÀNG PHONG * GV: Phaïm Nguyeãn
Só Thaéng
Ngày so n: 17 / 10/ 2005ạ
Ti t 16: ếKI M TRA CH NG IỂ ƯƠ
I. M C TIÊU: Ụ
- Ki m tra s hi u bài c a h c sinh.ể ự ể ủ ọ
- Bi t di n đ t đ nh lí và vi t GT, KL c a đ nh lí.ế ễ ạ ị ế ủ ị
- Bi t v n d ng các đ nh lí đ ch ng minh, suy lu n, tính toán s đo góc.ế ậ ụ ị ể ứ ậ ố
II. Đ BÀI: Ề
Bài 1: (2 đ)
Đánh d u “x” vào ô tr ng thích h p:ấ ố ợ
Câu N i dung ộĐúng Sai
1 Hai đ ng th ng c t nhau thì vuông góc.ườ ẳ ắ
2 Hai đ ng th ng cùng vuông góc v i đ ng th ng th ba thì chúng song song v i nhau.ườ ẳ ớ ườ ẳ ứ ớ
3 Hai góc đ i đ nh thì b ng nhau.ố ỉ ằ
4 Hai đ ng th ng song song là hai đ ng th ng không c t nhau.ườ ẳ ườ ẳ ắ
Bài 2: (2 đ)
Phát bi u đ nh lí, vi t GT, KL đ c di n t b i hình v sau:ể ị ế ượ ễ ả ở ẽ
a A
b B
Bài 3: (2,5 đ)
Ch ng minh đ nh lí sau: (Vi t GT, KL)ứ ị ế
Hai tia phân giác c a hai góc đ i đ nh là hai tia đ i nhau.ủ ố ỉ ố
Bài 4: (2,5 đ) t A
350
C x
1350
B y
Bài 5: (1 đ)
A a0 x
a0+b0 C
B b0 y
II. ĐÁP ÁN VÀ BI U ĐI M:Ể Ể
Bài 1: (2 đ)
M i câu tr l i đúng đ c 0,5 đ:ỗ ả ờ ượ
Câu N i dung ộĐúng Sai
1 Hai đ ng th ng c t nhau thì vuông góc.ườ ẳ ắ x
2 Hai đ ng th ng cùng vuông góc v i đ ng th ng th ba thì chúng song song v i nhau.ườ ẳ ớ ườ ẳ ứ ớ x
3 Hai góc đ i đ nh thì b ng nhau.ố ỉ ằ x
4 Hai đ ng th ng song song là hai đ ng th ng không c t nhau.ườ ẳ ườ ẳ ắ x
Bài 2: (2 đ)
Phát bi u đúng đ nh lí đ c 1 đ, vi t đúng GT, KL đ c 1 đ:ể ị ượ ế ượ
Đ nh lí: N u m t đ ng th ng c t hai đ ng th ng mà trong các góc t o thành có m t c p góc so leị ế ộ ườ ẳ ắ ườ ẳ ạ ộ ặ
trong b ng nhau thì hai đ ng th ng đó song song nhau.ằ ườ ẳ
GT c c t a và b t i A và B A cắ ạ
µ
1 1
A B=
a 1
KL a // b 1
b B
Bài 3: (2,5 đ)
V hình đúng (0,5 đ), vi t đúng GT, KL đ c 0,5 đẽ ế ượ
HÌNH HOÏC 7
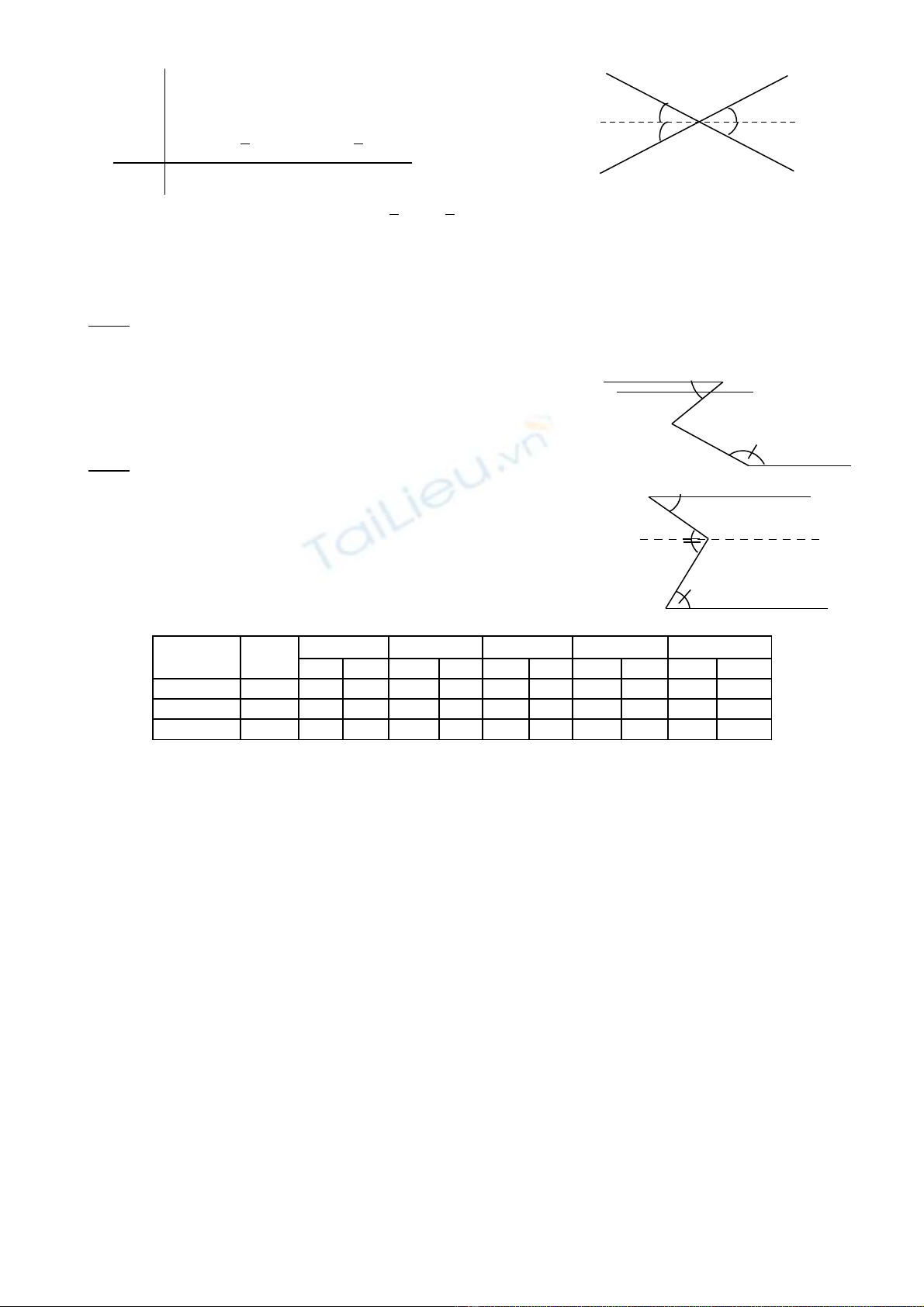
Cho hình vẽ bên. Biết :
·
·
·
0 0 0 0
xAC a ;CBy b ;ACB a b= = = +
.
Chứng minh rằng: Ax // By
TRÖÔØNG THCS LEÂ HOÀNG PHONG * GV: Phaïm Nguyeãn
Só Thaéng
GT
·
·
0
1 2 5
0
346
1 2 3 4
O O O 180
O O O 180
1 1
O O xOy;O O x'Oy'
2 2
+ + =
+ + =
= = = =
KL
0
1 5 3
O O O 180+ + =
Ch ng minh: T GT ứ ừ
·
·
1 3 4 2
1 1
O O O O xOy x'Oy'
2 2
= = = = =
(0,5 đ)
Do đó:
1 5 3 1 2 5
O O O O O O+ + = + +
(0,5 đ)
Mà :
0
1 2 5
O O O 180+ + =
0
1 5 3
O O O 180+ + =
(đpcm)
V y: Hai tia OM và ON đ i nhau. (0,5 đ)ậ ố
Bài 4: (2,5 đ)
Qua C v đ ng th ng a // Ax (0,5 đ)ẽ ườ ẳ
Suy ra:
(So le trong) (1) (0,5 đ)
Mà Ax // By a // By (0,5 đ)
Do đó:
µ
µ
0 0 0 0 0
2 1 2 1
C B 180 C 180 B 180 135 45+ = ⇒ = − = − =
(2) (0,5 đ)
T (1) và (2) suy ra: x = ừ
0 0 0
1 2
C C 35 45 80+ = + =
(0,5 đ)
Bài 5: (1 đ)
Qua C v đ ng th ng c // Ax (1) A aẽ ườ ẳ 0 x
·
0
1
C xAC a= =
(0,5 đ) c 1 C
Mà:
0 0 0 0 0 0
1 2 2
C C a b C a b a b+ = + ⇒ = + − =
a0+b0 2
M t khác: ặ
·
0
CBy b=
b0
Hai góc v trí so le trong nên c // By (2) B yở ị
T (1) và (2) suy ra: Ax // By (đpcm) (0,5 đ) ừ
IV. TH NG KÊ CH T L NG: Ố Ấ ƯỢ
IV. RÚT KINH NGHI M, B SUNG:Ệ Ổ
HÌNH HOÏC 7
L pớSĩ số9 - 10 7 - 8 5 - 6 3 - 4 0 2
SL % SL % SL % SL % SL %
x y’
1 5 3
M 2 6 4 N
x’ y’
x A
35 0 1
a C x 1
2 135 0
B 1
y