TỔNG VÀ HIỆU CỦA HAI VECTƠ(T1)
A-Mục tiêu:
1.Kiến thức:
-Học sinh biết cách dựng véctơ tổng của hai vectơ theo định nghĩa
và quy tắc hình bình hành
-Nắm được các tính chất của phép cộng hai véctơ
2.Kỹnăng:
-Rèn luyện kỹ năng xác định vectơ tổng của hai vectơ theo định
nghĩa và quy tắc hình bình hành
3.Thái độ:
-Giáo dục cho học sinh tính cẩn thận,chính xác
B-Phương pháp:
-Nêu vấn đề và giải quyết vấn đề
-Phương pháp trực quan
C-Chuẩn bị
1.Giáo viên:Giáo án,thước kẻ
2.Học sinh:Đã chuẩn bị bài theo yêu cầu
D-Tiến trình lên lớp:
I-Ổn định lớp:(1')Ổn định trật tư,nắm sỉ số
II-Kiểm tra bài cũ:(6')
-Cho lục giác đều ABCDEF,có tâm là O:
+Xác định các vectơ bằng vectơ
AB có điểm đầu là O
+Xác định các vectơ có độ dài bằng vectơ AB có điểm đầu
là O
III-Bài mới:
1.Đặt vấn đề:(1')Tổng của hai vectơ được xác định như thế nào,nó
co những tính chất như tổng các số không,ta đi vào bài mới để tìm hiểu
điều này
2.Triển khai bài dạy:
HOẠT ĐỘNG THẦY VÀ TRÒ NỘI DUNG KIẾN THỨC
Hoạt đông1(10') Tổng hai véctơ
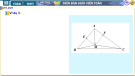
1.Tổng của hai véctơ:
GV:Hướng dẫn học sinh cách xác *)Định nghĩa:Cho hai véctơ a và
AB
a
b .Lấy một điểm A tuỳ ý,vẽ
BC
b
định vectơ tổng của hai vectơ
AC được gọi là
và .Vectơ
HS:Từ cách xây dựng của giáo
tổng của hai vectơ a và b .Ta kí viên rút ra định nghĩa cách xây
hiệu tổng của hai vectơ a và b là a dựng vectơ tổng của hai vectơ
+ b .Vây
AC = a + b
B
a
b
a
AB
BC
AC
a+b
C
b
A
GV:Nếu thì AB + BC
= AC không?
HS:Trả lời,giải thích
GV:Với cách định nghĩa trên thì
AB
BC
AC
với ba điểm M,N,P bất kì,ta có thể
MN bằng tổng của
-Nếu không suy ra biểu diễn véctơ
được AB + BC = AC những vectơ nào?
MN
MP
PN
-Với ba điểmM,N,P ta co thể biểu HS:
MN
MP
PN
diễn Hoạt động2(15')
GV:Hướng dẫn học sinh xây dựng
quy tắc hinh bình hành
Quy tắc hình bình hành
2.Quy tắc hình bình hành:
AC bằng véctơ nào?
GV:Vectơ
HS:Bằng vectơ
BD
D
B
AC
AB
GV:Khi đó bằng vectơ
A
C
nào?
AB
AC
AD
HS:
GV:Giới thiệu quy tắc hình bình
hành
AB
-Nếu ABCD là hình bình hành thì
AC
AD
*)Ví dụ:Cho ABC ,
A =90o,AB=
GV:Đọc đề và ghi ví dụ lên bảng 4cm ,AC=6cm.Xác định và tính
độ dài các vectơ sau
BA
AC
HS:Vẽ hình và suy nghĩ cách làm i,
AB
AC
bài toán
A
BA
AC
3
4
ii,
I
B
C
D
GV: =? Giải
HS:
BC và tính độ dài BC
BA
AC
BC
2
2
BC
543
i,Ta có: =
= BC = (cm) GV:Độ dài AD bằng bao nhiêu?
AB
AC
HS:AD = BC =
AD
ii,
AD
BC
HS:AD=2AO,từ đó tính được độ
= =BC= 5(cm) dài vectơ AD
Tính chất của phép cộng các vectơ Hoạt động3(7')
3.Tính chất của phép cộng các HS:Nhắc lại các tính chất của
cba ,,
vectơ: phép cộng các số
ba
ab
Với ba vectơ tuỳ ý ta có: GV:Giới thiệu các tính chất của
bá
)
a
c
(
b
c
)
i, (tính chất giao hoán) phép cộng các véctơ và hướng dẫn
học sinh chứng minh các tính chất ii,( (tính chất kết
oa
ao
đó dựa vào các hình vẽ hợp)
iii, (tính chất của véctơ-
không)
IV.Củng cố:(3')
-Nhắc lai phép cộng các vectơ theo định nghĩa và quy tắc hình
bình hành
-Khi nào thì dùng định nghĩa và khi nào thì dùng quy tắc hình
bình hành để
các vectơ
V.Dặn dò:(2')
-Nắm vững cách xác định vectơ tổng của hai vectơ
-Làm bài tập 2,4,7a,10/SGK
-Chuẩn bi bài mới:
+ Hai vectơ gọi là đối nhau khi nào
+Tìm các vectơ đối nhau trong hình bình hành ABCD
VI.Bổ sung và rút kinh nghiệm: