Ch−¬ng 4
§æi chiÒu dßng ®iÖn
4-1. §¹i c−¬ng
Nh− ®· tr×nh bµy ë ch−¬ng 2, khi chuyÓn ®éng trong tõ tr−êng cña mét cùc tõ, mçi
phÇn tö cña d©y quÊn phÇn øng thuéc vµo mét nh¸nh song song vµ dßng ®iÖn i− trong
nã cã chiÒu nhÊt ®Þnh. Lóc c¸c c¹nh cña phÇn tö ®i vµo vïng trung tÝnh th× phÇn tö bÞ
chæi than nèi ng¾n m¹ch, dßng ®iÖn trong phÇn tö thay ®æi ®Ó sau ®ã khi phÇn tö b−íc
sang ranh giíi cña cùc kÕ tiÕp vµ chuyÓn sang nh¸nh song song kh¸c, dßng ®iÖn trong
nã cã chiÒu ng−îc l¹i - i− (h×nh 4-1). Qu¸ tr×nh ®æi chiÒu cña dßng ®iÖn khi phÇn tö di
®éng trong vïng trung tÝnh vµ bÞ chæi than nèi ng¾n m¹ch ®−îc gäi lµ sù ®æi chiÒu.
32
H
×nh
4
-1.
Q
u¸ tr×nh ®æi chiÒu
1 2 3
a b c
i−
2
i
−
i1 i2
t = 0
a
)
i− i− i−
1 2 3
a b c
i
2
i
−
o < t < T®c
A
B
b)
i1 i2
i
i
−
i
−
1 2 3
a b c
i−
i−
i−
i−
i1 i2
2
i
−
t = T®c
c
)
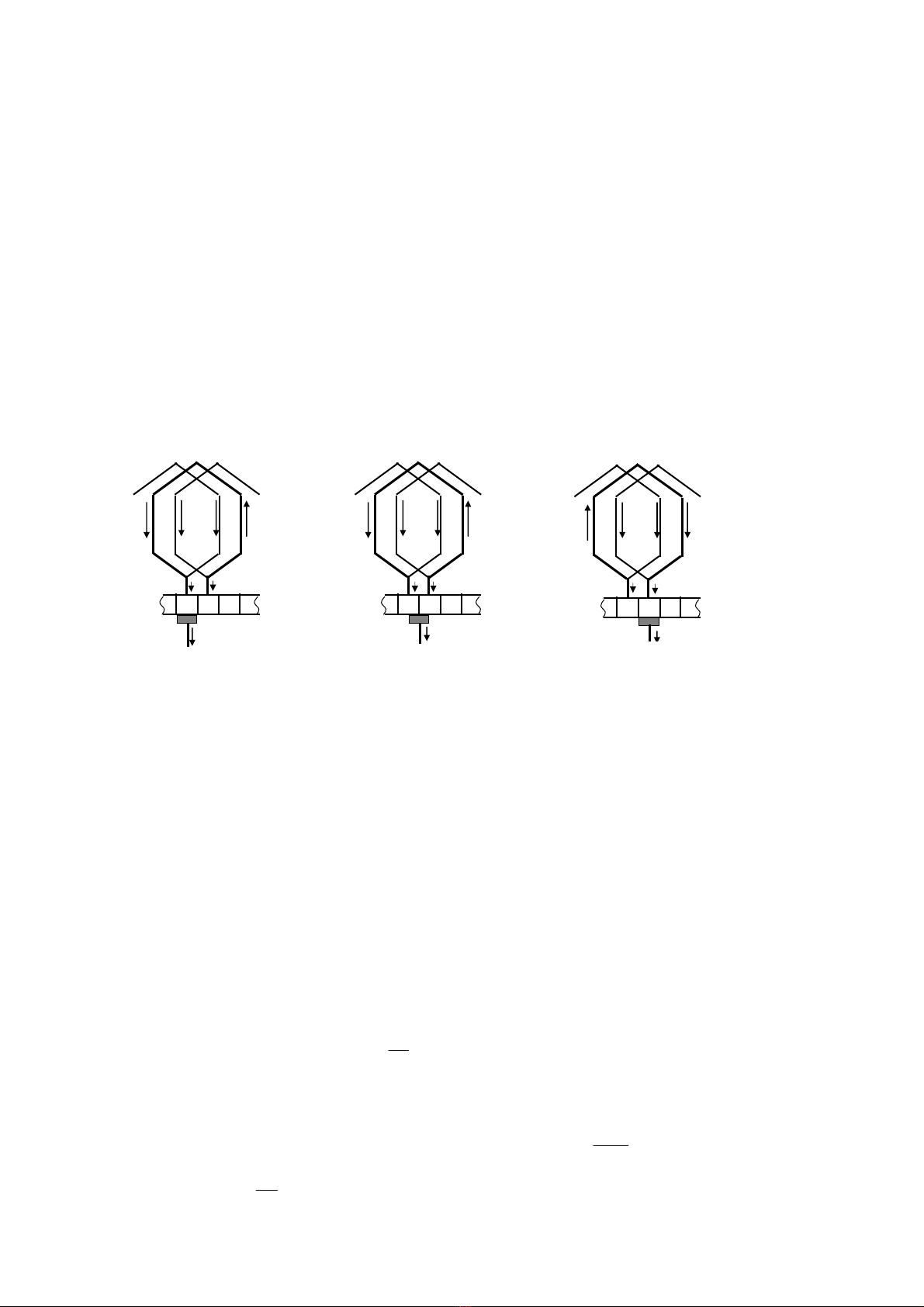
§Ó cã kh¸i niÖm cô thÓ, h×nh 4-1 tr×nh bµy qu¸ tr×nh ®æi chiÒu dßng ®iÖn trong
phÇn tö b cña d©y quÊn xÕp ®¬n. Ta thÊy khi chæi than phñ hoµn toµn lªn phiÕn gãp 1
(h×nh 4-1a) dßng ®iÖn trong phÇn tö b gi¶ sö cã chiÒu + i−. Khi chæi than hoµn toµn
t¸ch khái phiÕn gãp 1 (h×nh 4-1c) th× dßng ®iÖn trong phÇn tö b cã chiÒu ng−îc l¹i (-i−).
ë c¸c vÞ trÝ trung gian, chæi than tiÕp xóc víi c¶ hai phiÕn ®æi chiÒu 1 vµ 2 khiÕn cho
phÇn tö bÞ nèi t¾t vµ dßng ®iÖn trong nã biÕn ®æi theo nh÷ng quy luËt nhÊt ®Þnh, phô
thuéc vµo qu¸ tr×nh qu¸ ®é ®iÖn tõ x¶y ra trong vµ xung quanh phÇn tö ®æi chiÒu.
Qu¸ tr×nh ®æi chiÒu cña dßng ®iÖn trong mçi phÇn tö tån t¹i trong mét thêi gian rÊt
ng¾n. Kho¶ng thêi gian ®Ó dßng ®iÖn hoµn thµnh viÖc ®æi chiÒu gäi lµ chu kú ®æi
chiÒu, ký hiÖu T®c. §ã lµ thêi gian cÇn thiÕt ®Ó vµnh gãp quay ®i mét gãc t−¬ng øng víi
chiÒu réng cña chæi ®iÖn, nghÜa lµ:
T®c =
G
c
v
b (4-1)
trong ®ã: vG - lµ tèc ®é dµi cña vµnh gãp; bc - chiÒu réng cña chæi than.
NÕu chóng ta ký hiÖu: DG - ®−êng kÝnh cña vµnh gãp; G
D
bG
G
π
=- b−íc vµnh gãp;
G - sè phiÕn gãp;
G
c
Gb
b
=
β
vµ biÕt r»ng tèc ®é dµi cña vµnh gãp lµ:
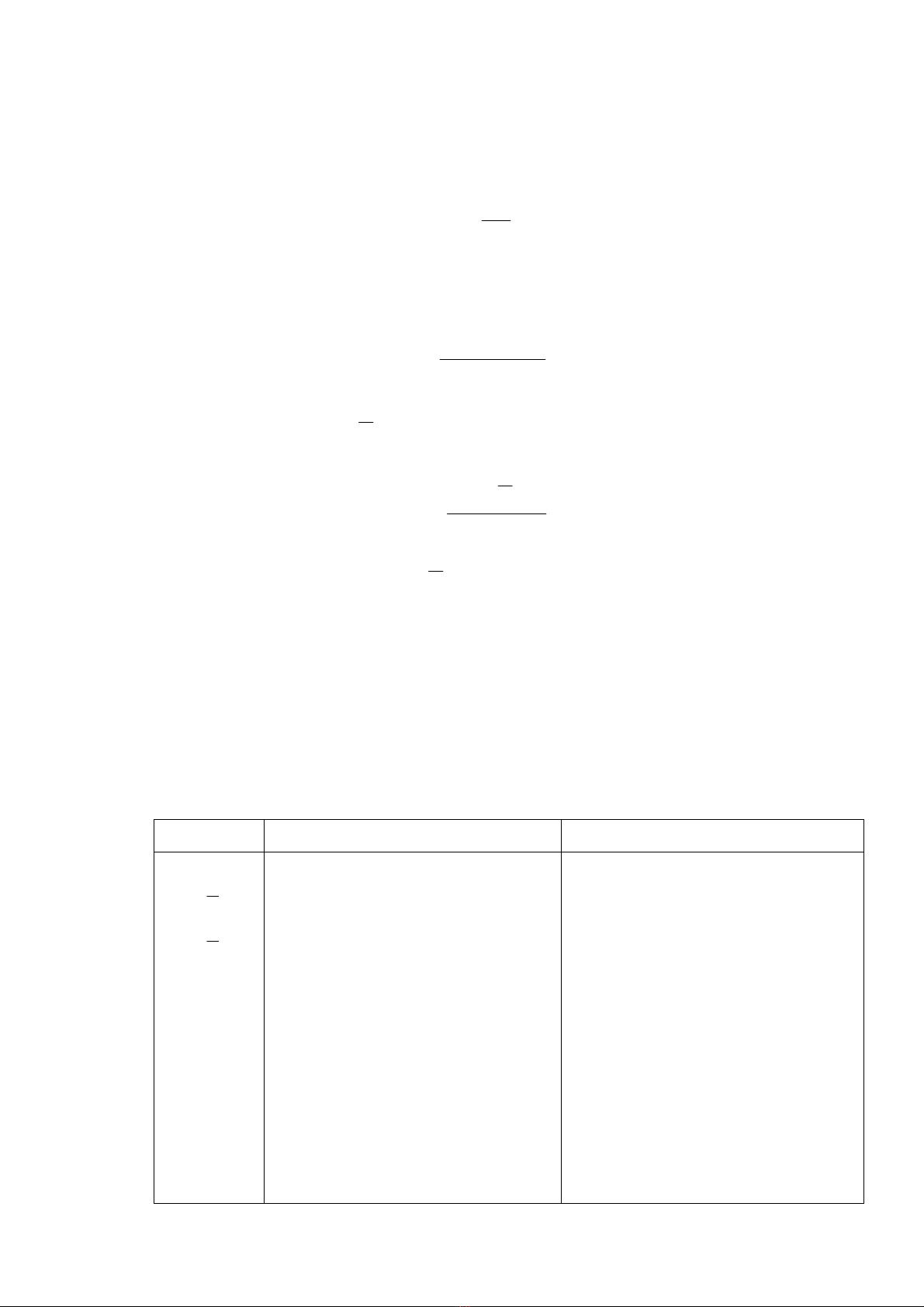
vG = πDGn = bG.G.n (4-2)
trong ®ã n lµ tèc ®é quay cña vµnh gãp, th× chu kú ®æi chiÒu ë d©y quÊn xÕp ®¬n (h×nh
4-1) cã d¹ng:
n
G
TGdc .
1
β
= (4-3a)
ë lo¹i d©y quÊn xÕp phøc t¹p (môc 2.3) cã b−íc vµnh gãp yG = m (m ≠ 1), gi÷a ®Çu
vµ cuèi cña mçi phÇn tö cã (m - 1) phiÕn gãp. Nh− vËy phÇn tö sÏ bÞ chæi than nèi ng¾n
m¹ch trong kho¶ng thêi gian ®Ó vµnh gãp quay ®i mét cung bc - (m - 1)bG, do ®ã:
G
Gc
dc v
bmb
T)1( −−
=
Thay bc = βG.bG, p
a
m= vµ vG ë biÓu thøc (4-2) ta sÏ thu ®−îc:
nG
p
a
T
G
dc .
1⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛−−
=
β
(4-3b)
Râ rµng ë d©y quÊn xÕp ®¬n 1=
p
a nªn biÓu thøc (4-3b) sÏ cã d¹ng nh− biÓu thøc
(4-3a).
Khi m¸y ®iÖn lµm viÖc, c¸c phÇn tö liªn tiÕp tiÕn hµnh ®æi chiÒu vµ trong thùc tÕ
T®c ≈ 0,001s nªn qu¸ tr×nh ®æi chiÒu diÔn ra tuÇn hoµn víi tÇn sè 1000 ÷ 3000 Hz.
ViÖc ®æi chiÒu cã thuËn lîi hay kh«ng, nãi c¸ch kh¸c lµ chÊt l−îng cña sù ®æi
chiÒu phô thuéc vµo nhiÒu yÕu tè c¬ vµ ®iÖn tõ. Sù ®æi chiÒu kÐm chÊt l−îng ®−îc biÓu
hiÖn bªn ngoµi bëi sù h×nh thµnh tia löa ®iÖn trªn bÒ mÆt vµnh gãp vµ d−íi chæi than.
Tiªu chuÈn Nhµ n−íc quy ®Þnh c¸c cÊp tia löa tr×nh bµy nh− ë b¶ng 4-1.
B¶ng 4-1. CÊp tia löa cña m¸y ®iÖn
CÊp tia löa §Æc ®iÓm T×nh tr¹ng chæi ®iÖn vµ vµnh gãp
1
4
1
1
Kh«ng cã tia löa
§èm löa yÕu ë mét phÇn chæi than
Kh«ng cã vÕt trªn vµnh gãp vµ
muéi than trªn c¸c chæi
2
1
1 Tia löa yÕu ë phÇn lín chæi than Cã vÕt trªn vµnh gãp nh−ng cã thÓ
chïi s¹ch b»ng dÇu, x¨ng.
Cã muéi trªn chæi.
2 Tia löa ë toµn bé chæi than chØ cho
phÐp ®èi víi t¶i xung hoÆc qu¸ t¶i
ng¾n h¹n.
Cã vÕt trªn vµnh gãp kh«ng thÓ
chïi s¹ch b»ng dÇu x¨ng vµ cã
muéi than trªn c¸c chæi.
3 Tia löa m¹nh vung ra ë toµn bé
chæi than. ChØ cho phÐp lóc më
m¸y trùc tiÕp víi ®iÒu kiÖn sau ®ã
vµnh gãp vµ chæi than vÉn ë tr¹ng
th¸i b×nh th−êng, cã thÓ tiÕp tôc
lµm viÖc ®−îc.
VÕt ®Ëm trªn vµnh gãp kh«ng thÓ
chïi s¹ch b»ng x¨ng dÇu, ch¸y
hoÆc háng chæi ®iÖn.
33

4-2. Qu¸ tr×nh ®æi chiÒu
4.2.1. Ph−¬ng tr×nh dßng ®iÖn
§Ó thÊy râ quy luËt biÕn ®æi cña dßng ®iÖn trong phÇn tö ®æi chiÒu vµ nguyªn nh©n
chñ yÕu ph¸t sinh tia löa, tõ ®ã nªu ra biÖn ph¸p c¶i thiÖn ®æi chiÒu, ta h·y nghiªn cøu
quy luËt ®æi chiÒu x¶y ra ë phÇn tö cña d©y quÊn xÕp ®¬n trªn h×nh 4-1b. BiÓu thøc cña
dßng ®iÖn trong bèi d©y ®æi chiÒu cã thÓ suy ra tõ c¸c ®Þnh luËt Kirhhoff viÕt cho bèi
d©y ®ã.
Theo ®Þnh luËt Kirhhoff thø hai viÕt cho m¹ch vßng cña bèi ®æi chiÒu ta cã:
i.rpt + i1(rd + rtx1) - i2(rd + rtx2) = Σe (4-4)
trong ®ã:
i - dßng ®iÖn ch¹y trong phÇn tö ®æi chiÒu (phÇn tö b trªn h×nh 4-1);
i1 , i2 - dßng ®iÖn ch¹y trªn c¸c d©y nèi víi c¸c phiÕn ®æi chiÒu 1 vµ 2;
rtx1 , rtx2 - lµ c¸c ®iÖn trë tiÕp xóc gi÷a chæi than víi c¸c phiÕn ®æi chiÒu 1 vµ 2;
rpt, rd - lµ ®iÖn trë cña phÇn tö, ®iÖn trë cña d©y nèi
Σe - tæng c¸c s.®.®. c¶m øng sinh ra trong phÇn tö ®æi chiÒu, bao gåm:
1. S.®.®. tù c¶m eL g©y ra do sù biÕn ®æi cña dßng ®iÖn i trong phÇn tö ®æi chiÒu.
2. S.®.®. hç c¶m eM sinh ra do ¶nh h−ëng cña sù ®æi chiÒu ®ång thêi cña c¸c phÇn
tö kh¸c n»m trong cïng mét r·nh.
3. S.®.®. ®æi chiÒu e®c sinh ra khi phÇn tö ®æi chiÒu chuyÓn ®éng trong tõ tr−êng
tæng hîp t¹i vïng trung tÝnh. Tõ tr−êng nµy do cùc tõ phô vµ ph¶n øng phÇn øng t¹o
thµnh.
C¸c s.®.®. eL vµ eM cã t¸c dông nh− nhau ®èi víi qu¸ tr×nh ®æi chiÒu vµ tæng cña
chóng ®−îc gäi lµ s.®.®. ph¶n kh¸ng: epk = eL + eM. §Ó qu¸ tr×nh ®æi chiÒu tiÕn hµnh
®−îc thuËn lîi, s.®.®. ®æi chiÒu e®c ph¶i lu«n lu«n ng−îc chiÒu víi epk nãi trªn. Tuú theo
quan hÖ gi÷a hai lo¹i s.®.®. ®ã, tÝnh chÊt cña qu¸ tr×nh ®ã sÏ ®−îc tr×nh bµy ë phÇn sau.
Theo ®Þnh luËt Kirhhoff thø nhÊt, cã thÓ viÕt ph−¬ng tr×nh dßng ®iÖn lÇn l−ît t¹i
c¸c ®iÓm nót A vµ B (h×nh 4-1b) nh− sau:
(4-5)
⎭
⎬
⎫
=−−
=−+
0
0
2
1
iii
iii
u
u
Trªn thùc tÕ rtx1, rtx2 kh«ng nh÷ng phô thuéc vµo i1, i2 vµ thêi gian mµ cßn phô
thuéc vµo sù ®èt nãng cña chæi than vµ phiÕn ®æi chiÒu vµ c¶ hiÖn t−îng ®iÖn ph©n
d−íi mÆt chæi n÷a. H¬n n÷a tæng c¸c s.®.®. Σe còng khã x¸c ®Þnh ®−îc chÝnh x¸c nªn
d−íi ®©y ta chØ xÐt vÊn ®Ò ë møc ®é gÇn ®óng.
Víi gi¶ thiÕt rpt = rd = 0, thay trÞ sè cña i1 vµ i2 theo (4-5) vµo (4-4) ta ®−îc:
2121
12
txtx
u
txtx
txtx
rr
e
i
rr
rr
i+
+
+
−
=
∑
, (4-6)
34

Sè h¹ng thø nhÊt cña biÓu thøc (4-6) lµ thµnh phÇn c¬ b¶n cña dßng ®iÖn ®æi chiÒu
icb, sè h¹ng thø hai lµ thµnh phÇn phô iph.
Víi gi¶ thiÕt rpt = rd = 0 th× râ rµng (rtx1 + rtx2) lµ tæng sè ®iÖn trë cña phÇn tö ®æi
chiÒu khi bÞ chæi than nèi ng¾n m¹ch. V× vËy dßng ®iÖn phô iph chÝnh lµ dßng ®iÖn
ng¾n m¹ch trong phÇn tö g©y nªn bëi tæng c¸c s.®.®. Σe.
Gi¶ thiÕt r»ng c¸c ®iÖn trë rtx1 vµ rtx2 tØ lÖ nghÞch víi c¸c bÒ mÆt tiÕp xóc Stx1 vµ Stx2
gi÷a chæi than víi c¸c phiÕn ®æi chiÒu 1 vµ 2. NÕu cho r»ng qu¸ tr×nh ®æi chiÒu b¾t ®Çu
khi t = 0 vµ kÕt thóc khi t = T®c víi ®iÒu kiÖn bc = bG th×:
S
T
tT
S
dc
dc
tx
−
=
1 (4-7)
S
T
t
S
dc
tx =
2 (4-8)
trong ®ã: S lµ bÒ mÆt tiÕp xóc toµn phÇn gi÷a chèi than vµ phiÕn gãp.
Gäi ®iÖn trë tiÕp xóc toµn phÇn øng víi mÆt tiÕp xóc toµn phÇn lµ rtx, ta cã:
tx
dc
dc
tx
tx
tx r
tT
T
r
S
S
r−
==
1
1 (4-9a)
tx
dc
tx
tx
tx r
t
T
r
S
S
r==
2
2 (4-9b)
Thay c¸c trÞ sè rtx1 vµ rtx2 võa t×m ®−îc vµo (4-6) ta cã quan hÖ gi÷a dßng ®iÖn i
trong phÇn tö ®æi chiÒu vµ thêi gian t nh− sau:
n
u
dc r
e
i
T
t
i
∑
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛−= ,
2
1 (4-10a)
trong ®ã: tx
dc
dc
txtxn r
tTt
T
rrr )(
2
21 −
=+= (4-10b)
4.2.2. X¸c ®Þnh c¸c s.®.®. trong phÇn tö ®æi chiÒu
§Ó ®¶m b¶o ®iÒu kiÖn ®æi chiÒu b×nh th−êng cña m¸y, khi thiÕt kÕ cÇn ph¶i x¸c
®Þnh c¸c s.®.®. sinh ra trong phÇn tö ®æi chiÒu ®Ó giíi h¹n chóng trong mét ph¹m vi
nhÊt ®Þnh. D−íi ®©y ta sÏ lÇn l−ît tÝnh c¸c s.®.®. ®ã.
a. S.®.®. tù c¶m eL
S.®.®. tù c¶m eL cã d¹ng:
dt
di
LeL−= (4-11)
trong ®ã: L - hÖ sè tù c¶m cña phÇn tö.
V× qua qu¸ tr×nh ®æi chiÒu, dßng ®iÖn biÕn ®æi tõ + i− ®Õn - i− nªn 0<
dt
di , do ®ã
eL > 0 vµ lµm cho sù thay ®æi cña dßng ®iÖn trong phÇn tö chËm dÇn.
Gi¸ trÞ trung b×nh cña s.®.®. tù c¶m trong chu kú ®æi chiÒu lµ:
35

dc
u
Ltb T
Li
e,
2
= (4-12)
b. S.®.®. hç c¶m eM
Cïng mét lóc víi sù ®æi chiÒu dßng ®iÖn trong phÇn tö ®ang xÐt, sù ®æi chiÒu còng
x¶y ra ë mét sè phÇn tö kh¸c. ë d©y quÊn xÕp ®¬n hai líp b−íc ®ñ, sù ®æi chiÒu x¶y ra
®ång thêi trong c¸c c¹nh t¸c dông cïng n»m trong mét r·nh. H¬n n÷a, th−êng bc > bG
vµ c¸c chæi than nèi ng¾n m¹ch vµi phÇn tö liªn tiÕp nhau cã c¹nh n»m trong mét r·nh,
nªn c¸c phÇn tö cïng tham gia ®æi chiÒu ®ã cã sù liªn hÖ hç c¶m rÊt m¹nh. V× vËy
trong phÇn tö tham gia ®æi chiÒu ®ang xÐt, ngoµi s.®.®. tù c¶m cßn cã s.®.®. hç c¶m:
dt
di
Mee n
n
n
n
M
n
M11 Σ−=Σ= (4-13)
trong ®ã: Mn - hÖ sè hç c¶m gi÷a phÇn tö ®ang xÐt víi phÇn tö thø n;
in - dßng ®iÖn trong bèi thø n.
S.®.®. hç c¶m eM còng cã t¸c dông ®èi víi qu¸ tr×nh ®æi chiÒu gièng nh− s.®.®. tù
c¶m eL. TrÞ sè trung b×nh cña s.®.®. hç c¶m b»ng:
n
dc
u
Mtb M
T
i
eΣ= ,
2 (4-14)
c. S.®.®. ph¶n kh¸ng
V× eL vµ eM cã tÝnh chÊt gièng nhau (®Òu lµm chËm qu¸ tr×nh ®æi chiÒu) nªn tæng
cña chóng gäi lµ s.®.®. ph¶n kh¸ng epk. S.®.®. ph¶n kh¸ng trung b×nh b»ng:
epktb = eLtb + eMtb (4-15)
d. S.®.®. ®æi chiÒu e®c
Gäi B®c lµ tõ c¶m tæng hîp cña tõ tr−êng cùc tõ phô vµ tõ tr−êng cña phÇn øng t¹i
vïng trung tÝnh (cßn gäi lµ tõ c¶m ®æi chiÒu) th× biÓu thøc s.®.®. ®æi chiÒu do tõ c¶m
nµy sinh ra b»ng:
e®c = 2B®c.ws.l®c. v− (4-16)
trong ®ã: l®c lµ chiÒu dµi cña thanh dÉn c¾t ®−êng søc cña tõ tr−êng ®æi chiÒu;
ws - sè vßng d©y cña bèi ®æi chiÒu;
v− - tèc ®é dµi cña phÇn øng.
ChiÒu cña s.®.®. ®æi chiÒu phô thuéc vµo chiÒu cña tõ tr−êng ®æi chiÒu vµ chiÒu
quay cña phÇn øng vµ ®−îc x¸c ®Þnh theo quy t¾c bµn tay ph¶i. V× vËy mµ e®c cã thÓ
cïng chiÒu hoÆc ng−îc chiÒu víi epk.
4.2.3. C¸c lo¹i ®æi chiÒu
a. §æi chiÒu ®−êng th¼ng
Gi¶ sö s.®.®. ®æi chiÒu e®c c¶m øng trong phÇn tö ®æi chiÒu do t¸c dông cña c¸c tõ
tr−êng tæng hîp t¹i vïng trung tÝnh triÖt tiªu ®−îc hoµn toµn s.®.®. ph¶n kh¸ng epk,
nghÜa lµ Σe = 0, th× dßng ®iÖn phô trong phÇn tö ®æi chiÒu b»ng kh«ng vµ tõ ph−¬ng
tr×nh (4-10a) ta cã:
36























![Ngân hàng câu hỏi ôn tập Anten và truyền sóng [Năm]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250115/sanhobien01/135x160/18471768473368.jpg)


