Chöông trình Giaûng daïy Kinh teá Fulbright
Nieân khoùa 2003-2004 Phöông phaùp phaân tích
Baøi ñoïc Nhaäp moân kinh teá löôïng vôùi caùc öùng duïng
Chöông 2: OÂn laïi xaùc suaát vaø thoáng keâ
Ramu Ramanathan 49 Thuïc Ñoan/Haøo Thi
Sample standard deviation
Second central moment
Size of a test
Standard deviation (s.d.)
Standard error
Standardized normal
Standard normal distribution
Statistically independent
Statistical test
Student’s t-distribution
Test statistic
Two-sized test
Two-tailed test
Type I error
Type II error
Unbiased
Uncorrelated
Variance of the distribution
Z-score
Moâmen maãu
Ñoä leäch chuaån maãu
Moâmen trung taâm baäc 2
Kích thöôùc cuûa moät kieåm ñònh
Ñoä leäch chuaån
Sai soá chuaån
Chuaån chuaån hoùa
Phaân phoái chuaån chuaån hoùa
Ñoäc laäp thoáng keâ
Kieåm ñònh thoáng keâ
Phaân phoái Student t
Trò thoáng keâ kieåm ñònh
Kieåm ñònh hai phía
Kieåm ñònh hai ñaàu
Sai laàm loaïi I
Sai laàm loaïi II
Khoâng thieân leäch
Khoâng töông quan
Phöông sai cuûa moät phaân phoái
Giaù trò Z
2.A PHUÏ LUÏC
Caùc Keát Quaû Tính Toaùn Khaùc
2.A.1 Moät Soá Keát Quaû Höõu Ích Cuûa Pheùp Tính Toång
Pheùp tính toång ñöôïc söû duïng nhieàu trong xaùc suaát, thoáng keâ vaø kinh teá löôïng, vì vaäy, vieäc
toùm taét moät soá tính chaát cuûa pheùp tính toång laø raát caàn thieát. Toång X1 + X2 + … + Xn ñöôïc
theå hieän baèng kyù hieäu Σt = n
t = 1 Xt, vôùi n laø toång soá caùc soá haïng trong toång vaø Xt laø moät soá
haïng ñaëc tröng trong toång. Giaù trò trung bình soá hoïc cuûa caùc X thöôøng ñöôïc kyù hieäu laø X
_
= (∑Xt/n). Moät vaøi tính chaát ñôn giaûn nhöng raát höõu ích cuûa pheùp tính toång ñöôïc trình
baøy trong phaàn naøy.
Tính chaát 2.A.1
Neáu k laø moät haèng soá thì Σt = n
t = 1 k = nk
Vì coù n soá haïng, moãi soá haïng laø moät haèng soá k, keát quaû roõ raøng nhö treân.
Chöông trình Giaûng daïy Kinh teá Fulbright
Nieân khoùa 2003-2004 Phöông phaùp phaân tích
Baøi ñoïc Nhaäp moân kinh teá löôïng vôùi caùc öùng duïng
Chöông 2: OÂn laïi xaùc suaát vaø thoáng keâ
Ramu Ramanathan 50 Thuïc Ñoan/Haøo Thi
Tính chaát 2.A.2
Neáu k laø moät haèng soá, thì Σt = n
t = 1 kXt = kΣt = n
t = 1 Xt.
Vì moãi soá haïng coù moät haèng soá k, neân coù theå ñaët k laøm nhaân töû chung.
Tính chaát 2.A.3
(Xt + Yt) =
∑
t = n
t = 1Xt +
∑
t = n
t = 1Yt
Tính chaát 2.A.4
Neáu X
_ = (∑Xt) / n laø giaù trò trung bình, thì ∑
t = n
t = 1 (Xt –X
_ ) = 0.
Vì vaäy, toång caùc sai leäch so vôùi giaù trò trung bình laø baèng khoâng.
CHÖÙNG MINH
∑ (Xt – X
_ ) = ( ∑Xt) – (∑ X
_ ) = (∑Xt) – nX
_
vì X
_ ñeàu nhö nhau ñoái vôùi moãi giaù trò t. Nhöng töø ñònh nghóa cuûa X
_ , nX
_ = ∑Xt. Do ñoù,
hai soá haïng cuoái cuøng trieät tieâu laãn nhau vaø vì vaäy ∑(Xt – X
_ ) = 0.
2.A.2. Cöïc Ñaïi vaø Cöïc Tieåu
Vieäc öôùc löôïng caùc thoâng soá chöa bieát cuûa moät phaân phoái thöôøng lieân quan ñeán cöïc ñaïi
hoaëc cöïc tieåu moät soá haøm muïc tieâu. Ví duï, khi öôùc löôïng caùc moái quan heä, moät muïc tieâu
quan troïng laø tìm ñöôïc “moái quan heä phuø hôïp nhaát”, ñoù laø moái quan heä coù sai soá nhoû
nhaát. Trong phaàn naøy chuùng ta trình baøy caùc phöông phaùp cöïc ñaïi hoaëc cöïc tieåu caùc haøm
muïc tieâu; vieäc naøy ñaëc bieät höõu ích khi nhaø nghieân cöùu coù nhöõng raøng buoäc veà caùc vaán
ñeà nghieân cöùu. Caùc nguyeân lyù caên baûn tröôùc tieân ñöôïc nghieân cöùu ñoái vôùi tröôøng hôïp
ñôn giaûn, chæ lieân quan ñeán moät bieán vaø khoâng coù raøng buoäc naøo. Sau ñoù, caùc nguyeân lyù
naøy ñöôïc môû roäng cho nhieàu bieán vaø cho tröôøng hôïp coù raøng buoäc.
Caùc Haøm Soá, Ñaïo Haøm, Cöïc Ñaïi Vaø Cöïc Tieåu
Töông quan toång quaùt cuûa moät bieán phuï thuoäc (Y) vaø moät bieán ñoäc laäp (X) ñöôïc trình
baøy döôùi daïng moät haøm soá kyù hieäu baèng bieåu thöùc Y = F(X). Luùc naøy, chuùng ta chæ taäp
trung chuù yù caùc haøm soá lieân quan ñeán moät bieán ñôn. Chuùng ta seõ giaû söû laø F(X) laø haøm
lieân tuïc; nghóa laø, F(X) khoâng “nhaûy” khi X chæ thay ñoåi trong moät khoaûng xaùc ñònh.
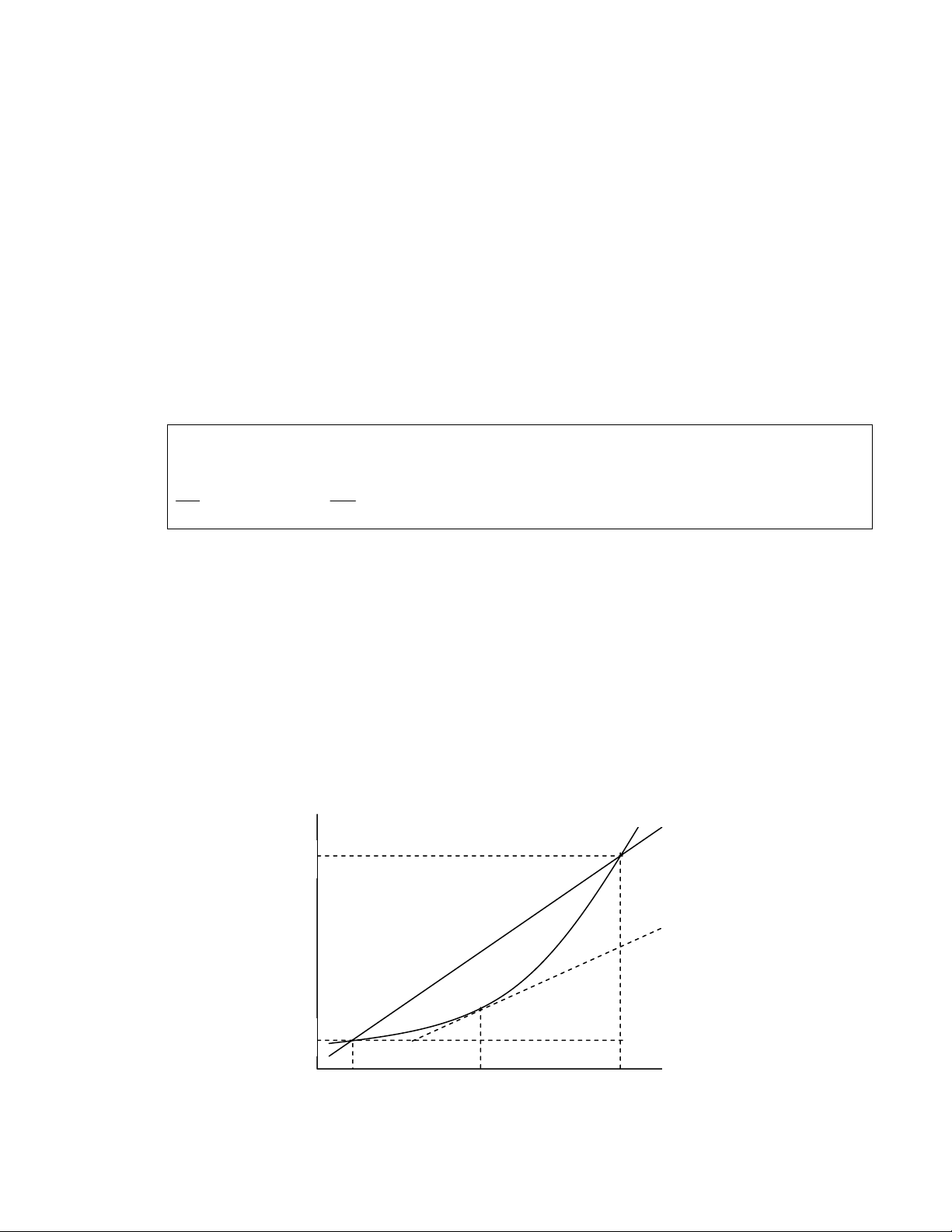
Moät haøm ñöôïc goïi laø taêng ñôn ñieäu neáu Y taêng khi vaø chæ khi X taêng (xem Hình 2.A.1).
Chöông trình Giaûng daïy Kinh teá Fulbright
Nieân khoùa 2003-2004 Phöông phaùp phaân tích
Baøi ñoïc Nhaäp moân kinh teá löôïng vôùi caùc öùng duïng
Chöông 2: OÂn laïi xaùc suaát vaø thoáng keâ
Ramu Ramanathan 51 Thuïc Ñoan/Haøo Thi
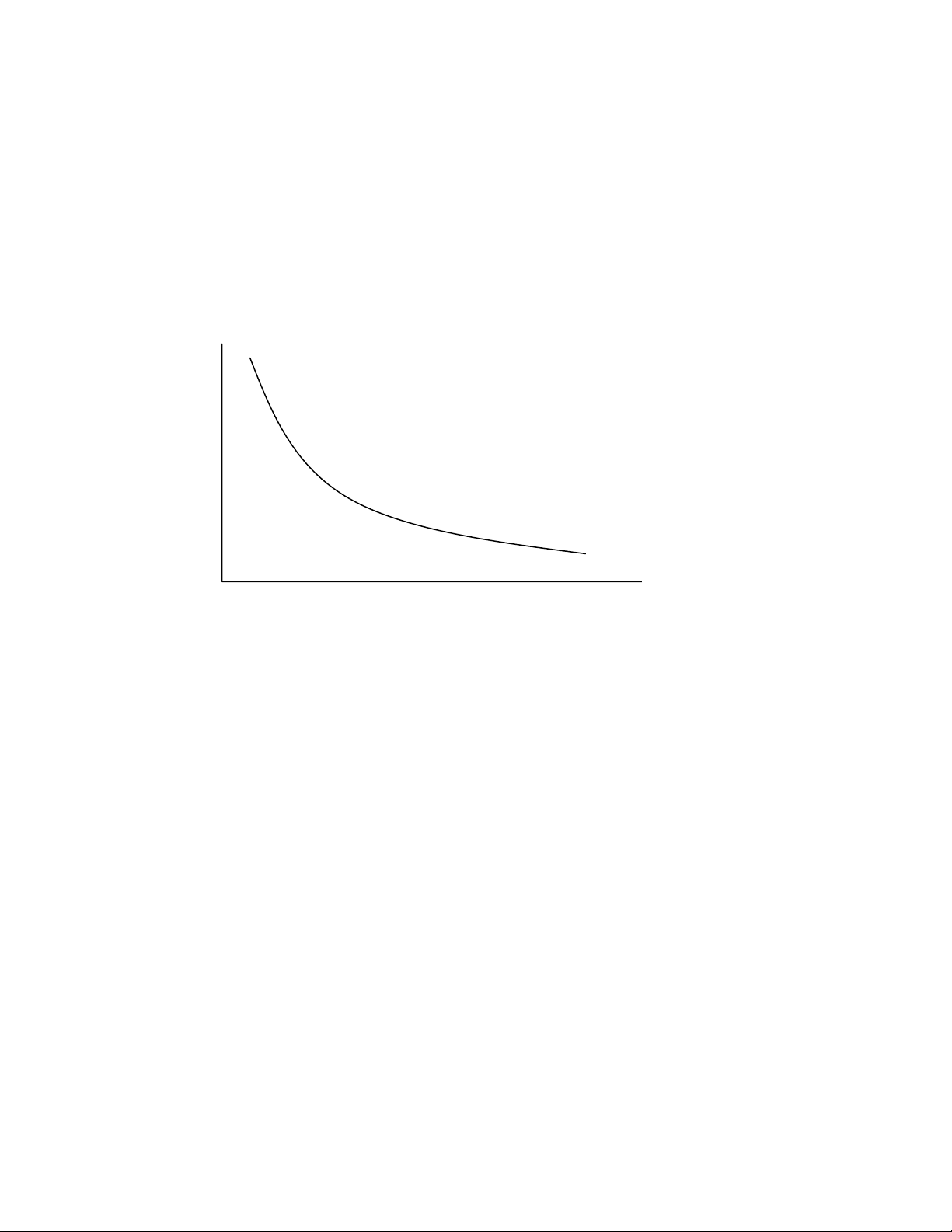
Moät ví duï veà haøm taêng ñôn ñieäu laø moät ñöôøng cung. Neáu Y giaûm khi X taêng, nhö trong
Hình 2.A.2, haøm soá ñöôïc goïi laø giaûm ñôn ñieäu (ñöôøng caàu laø moät ví duï). Trong Hình
2.A.1, xeùt hai ñieåm A vaø B coù toïa ñoä laø (X1, Y1) vaø (X2, Y2). Tyû soá (Y2 – Y1) / (X2 – X1)
laø ñoä doác cuûa ñöôøng thaúng noái hai ñieåm A vaø B, ñöôøng naøy caét ñoà thò haøm soá taïi A vaø B.
Tyû soá naøy ño löôøng söï thay ñoåi cuûa Y theo moät ñôn vò thay ñoåi cuûa X. Tyû soá naøy coøn
ñöôïc kyù hieäu laø ∆Y/∆X, vôùi ∆Y = Y2 – Y1 laø thay ñoåi cuûa Y vaø ∆X = X2 – X1 laø thay ñoåi
cuûa X. Giaû söû chuùng ta laøm cho ∆X ngaøy caøng nhoû hôn ñeán cuoái cuøng thì A vaø B gaëp
nhau taïi X. Cuoái cuøng, ñöôøng thaúng AB chæ tieáp xuùc vôùi ñoà thò cuûa F(X). Ñaây chính laø
tieáp tuyeán cuûa ñöôøng cong taïi ñieåm X; heä soá goùc cuûa tieáp tuyeán ñöôïc goïi laø ñaïo haøm cuûa
Y theo X. Heä soá naøy ñöôïc vieát döôùi daïng ñaïi soá nhö laø giôùi haïn cuûa ∆Y/∆X khi ∆X tieán
tôùi 0, vaø ñöôïc kyù hieäu laø dY/dX hoaëc laø F ’(x). Vì vaäy chuùng ta coù ñònh nghóa sau.
ÑÒNH NGHÓA 2.A.1
Ñaïo haøm cuûa Y theo X ñöôïc ñònh nghóa laø
dY
dX = F’(X) = lim
∆X→ 0 ∆Y
∆X vôùi ñieàu kieän toàn taïi giôùi haïn
Neáu toàn taïi giôùi haïn, F(X) ñöôïc goïi laø coù ñaïo haøm taïi X. Ví duï, giaû söû X laø toång löôïng
haøng hoaù saûn xuaát cuûa moät coâng ty vaø Y laø toång chi phí saûn xuaát löôïng haøng hoùa
naøy.Vaäy, F(X) laø haøm toång chi phí vaø ñaïo haøm, dY/dX, laø chi phí gia taêng khi saûn xuaát
theâm moät ñôn vò haøng hoùa, trong kinh teá löôïng ñaïi löôïng naøy ñöôïc goïi laø chi phí caän
bieân. Töø Hình 2.A.1 vaø 2.A.2 caàn löu yù laø ñaïo haøm F’(X) khoâng nhaát thieát phaûi laø haèng
soá nhöng phaûi phuï thuoäc vaøo giaù trò X maø taïi giaù trò ñoù ñaïo haøm ñöôïc tính. Do ñoù chuùng
ta coù theå laáy ñaïo haøm F’(X) moät laàn nöõa vaø ñöôïc F”(X) = d2Y/dX2, mieãn laø ñaïo haøm baäc
hai naøy toàn taïi.
} Hình 2.A.1 Haøm Soá Taêng Ñôn Ñieäu
F(X)
B
(X1, Y1)
A
Y2
Y1
X1 X X2
(X2, Y2)
F(X)
X
Chöông trình Giaûng daïy Kinh teá Fulbright
Nieân khoùa 2003-2004 Phöông phaùp phaân tích
Baøi ñoïc Nhaäp moân kinh teá löôïng vôùi caùc öùng duïng
Chöông 2: OÂn laïi xaùc suaát vaø thoáng keâ
Ramu Ramanathan 52 Thuïc Ñoan/Haøo Thi
} Hình 2.A.2 Haøm Soá Giaûm Ñôn Ñieäu
Trong Hình 2.A.1 ñaïo haøm döông ñoái vôùi moïi X trong mieàn xaùc ñònh cuûa F(X).
Töông töï, ñaïo haøm naøy luoân aâm trong Hình 2.A.2. Chuùng ta ñaõ thaáy ñoái vôùi moät haøm
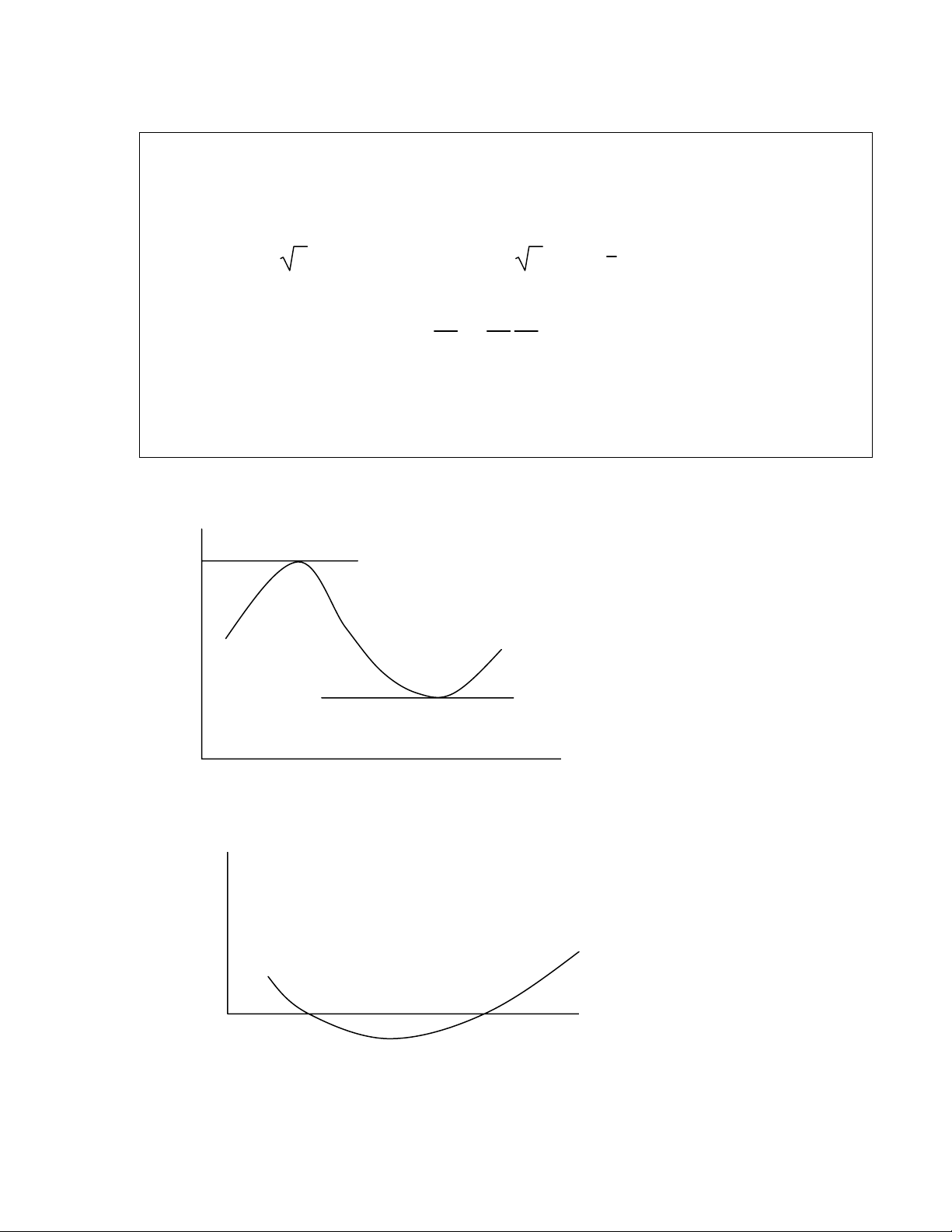
ñôn ñieäu ñaïo haøm luoân luoân coù cuøng moät daáu. Trong Hình 2.A.3a chuùng ta löu yù laø F(X)
khoâng phaûi laø haøm ñôn ñieäu maø laàn löôït taêng roài giaûm (ví duï nhö tyû leä thaát nghieäp). Ñaàu
tieân, heä soá goùc laø döông, sau ñoù chuyeån sang aâm vaø sau ñoù laïi trôû laïi döông. Caùc ñieåm A
vaø B coù tính chaát laø heä soá goùc cuûa tieáp tuyeán baèng 0. Vì vaäy, F’(X) = 0 taïi nhöõng ñieåm
naøy. Chuùng ta löu yù laø taïi A, F(X) ñaït cöïc ñaïi cuïc boä vaø taïi B haøm soá ñaït cöïc tieåu cuïc
boä. Moät ñieàu kieän caàn ñeå coù cöïc trò cuïc boä (nghóa laø cöïc ñaïi hoaëc cöïc tieåu) laø ñaïo haøm
baäc nhaát F’(X) phaûi baèng 0. Ñieàu kieän naøy, ñöôïc goïi laø ñieàu kieän baäc nhaát, khoâng phaûi laø
ñieàu kieän ñuû ñeå xaùc ñònh xem F(X) ñaït cöïc ñaïi hay cöïc tieåu. Hình 2.A.3b bieåu dieãn
F’(X), vaø chuùng ta löu yù laø ñaïo haøm naøy ñaàu tieân thi giaûm nhöng sau ñoù laïi taêng. Ñoä doác
cuûa F’(X) laø ñaïo haøm baäc hai F”(X) coù giaù trò aâm taïi A vaø döông taïi B. Ñeå phaân bieät
giöõa moät cöïc ñaïi vaø moät cöïc tieåu, chuùng ta caàn ñieàu kieän baäc hai laø ñaïo haøm baäc hai
F”(X) phaûi aâm taïi ñieåm maø taïi ñoù ñaïo haøm baäc nhaát F’(X) = 0 thì haøm F(X) môùi ñaït cöïc
ñaïi. Ñeå haøm soá ñaït cöïc tieåu thì ñieàu kieän baäc hai laø F”(X) döông taïi ñieåm maø F’(X) = 0.
Chuùng ta phaùt bieåu maø khoâng caàn chöùng minh moät soá keát quaû höõu ích töø caùc ñaïo
haøm.
Tính chaát 2.A.5
F(X)
F(X)
X
Chöông trình Giaûng daïy Kinh teá Fulbright
Nieân khoùa 2003-2004 Phöông phaùp phaân tích
Baøi ñoïc Nhaäp moân kinh teá löôïng vôùi caùc öùng duïng
Chöông 2: OÂn laïi xaùc suaát vaø thoáng keâ
Ramu Ramanathan 53 Thuïc Ñoan/Haøo Thi
a. Ñaïo haøm cuûa moät haèng soá baèng khoâng
b. Ñaïo haøm cuûa toång F(X) + G(X) baèng toång cuûa caùc ñaïo haøm F’(X) + G’(X).
c. Neáu a laø moät haèng soá, ñaïo haøm cuûa aF(X) baèng aF’(X).
d. Ñaïo haøm cuûa haøm soá muõ Xm baèng mXm –1. Moät tröôøng hôïp ñaëc bieät cuûa tính chaát naøy laø
ñaïo haøm cuûa X (nghóa laø X1/2 ) baèng 1 / (2 X ), hoaëc 1
2 X-1/2. Töông töï, ñaïo haøm cuûa 1
/ X (nghóa laø X-1) baèng −1 / X2 (nghóa laø −X− 2).
e. Neáu Y = F(Z) vaø Z = G(X) thì dY
dX = dY
dZ dZ
dX = F’G’ = F’(Z) G’(X) = F’[G(X)]G’(X).
[Keát quaû naøy ñöôïc goïi laø qui luaät daây chuyeàn cuûa vi phaân.]
f. Theo nguyeân taéc nhaân sai phaân, ñaïo haøm cuûa F(X)G(X) baèng F(X)G’(X) + G(X)F’(X).
g. Theo nguyeân taéc chia sai phaân, ñaïo haøm cuûa tyû soá F(X) / G(X) baèng [G(X)F’(X) −
F(X)G’(X)] / [G(X)]2.
} Hình 2.A.3
a. Ñoà thò haøm soá khoâng ñôn ñieäu
b. Ñoà thò F’(X)
B
A
F(X)
F(X)
X
A B
F(X)
X
F(X)