1
OÂN THI CAO HOÏC MOÂN TOAÙN KINH TEÁ
(Bieân soaïn: Traàn Ngoïc Hoäi - 2007)
PHAÀN III: THOÁNG KEÂ
A- ÖÔÙC LÖÔÏNG
§1. CAÙC ÑAËC TRÖNG MAÃU
1.1. Baûng soá lieäu
Khi khaûo saùt ñaùm ñoâng X ta thu thaäp soá lieäu cuûa maãu côõ n:
(X1, X2,…, Xn) vaø thöôøng laäp baûng soá lieäu theo caùc daïng sau:
Daïng 1: Lieät keâ döôùi daïng:
x1, x2,…, xn
trong ñoù moãi soá lieäu coù theå laëp laïi nhieàu laàn.
Daïng 2: Laäp baûng coù daïng:
Xi x
1 x
2 ……………………….. xk
ni n
1 n
2 …………………………. nk
trong ñoù x1 < x2 <… < xk vaø moãi soá lieäu xi xuaát hieän ni laàn.
Daïng 3: Laäp baûng coù daïng:
Xi x
1- x2x2- x3……………………….. xk- xk+1
ni n
1 n
2 …………………………. nk
trong ñoù x1 < x2 <… < xk < xk+1 vaø moãi nöûa khoaûng [xi; xi+1)
(tröø caùi cuoái cuøng laø ñoaïn [xk; xk+1]) chöùa ni soá lieäu.
Khi xöû lyù soá lieäu ta seõ ñöa soá lieäu veà Daïng 2.
Coù theå ñöa Daïng 1 veà Daïng 2 baèng caùch thoáng keâ laïi.
2
Daïng 3 ñöôïc ñöa veà Daïng 2 baèng caùch thay caùc khoaûng
xi-xi+1 baèng giaù trò trung bình cuûa hai ñaàu muùt 2
'1+
+
=ii
i
xx
x.
Trong caùc phaàn sau, ta xeùt maãu cuûa ñaùm ñoâng X coù daïng 2.
1.2. Kyø voïng maãu.
1) Ñònh nghóa: Kyø voïng maãu hay Trung bình maãu cuûa
ñaùm ñoâng X öùng vôùi maãu (X1, X2,…, Xn), kí hieäu XX n hay
laø ñaïi löôïng ngaãu nhieân ñònh bôûi:
∑
=
=k
i
ii nX
n
X
1
1
2) YÙ nghóa:
Khi ∞→n kyø voïng maãu n
X hoäi tuï veà kyø voïng
ñaùm ñoâng μ = M(X). Do ñoù khi n khaù lôùn ta xaáp xæ:
n
XXM
≈
=
)(
μ
1.3. Phöông sai maãu vaø ñoä leäch maãu
1) Ñònh nghóa:
Phöông sai maãu cuûa ñaùm ñoâng X öùng vôùi maãu
(X1, X2,…, Xn), kí hieäu
2
S(coøn kí hieäu laø 2
n
x
σ
hay 2
n
σ) laø ñaïi
löôïng ngaãu nhieân ñònh bôûi:
k
222
ii
i1
1
SXn(X)
n
=
=−
∑
Caên baäc hai cuûa phöông sai maãu cuûa X goïi laø ñoä leäch
maãu, kí hieäu
S (coøn kí hieäu laø n
x
σ
hay n
σ
):
k22
ii
i1
1
SXn(X)
n=
=−
∑
2) Phöông sai maãu vaø ñoä leäch maãu hieäu chænh
Phöông sai maãu hieäu chænh cuûa ñaùm ñoâng X öùng vôùi
maãu (X1, X2,…, Xn), kí hieäu 2
S(coøn kí hieäu laø 2
n1
x
−
hay 2
n1−
σ)
laø ñaïi löôïng ngaãu nhieân ñònh bôûi:
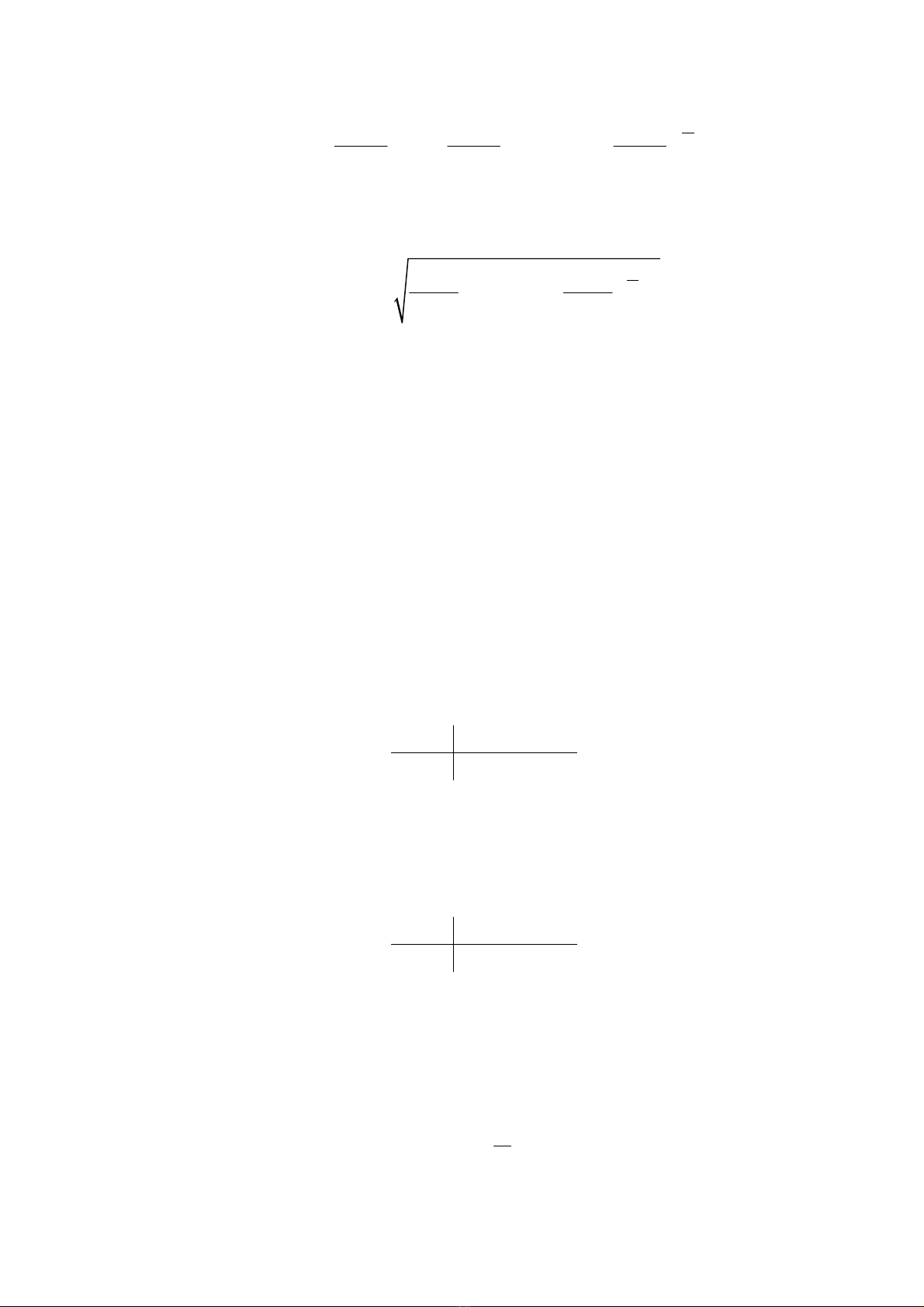
3
k
2
222
ii
i1
n1 n
SS Xn(X)
n1 n1 n1
=
== −
−− −
∑
Caên baäc hai cuûa phöông sai maãu hieäu chænh cuûa X goïi laø
ñoä leäch maãu hieäu chænh, S (coøn kí hieäu laø n1
x
−
hay n1−
σ):
k22
ii
i1
1n
SXn(X)
n1 n1
=
=−
−−
∑
.
3) YÙ nghóa:
Khi ∞→n phöông sai maãu hieäu chænh hoäi tuï veà
phöông sai ñaùm ñoâng σ2 = D(X). Do ñoù khi n khaù lôùn ta xaáp xæ:
22
D(X) S
σ
=≈
1.4. Phöông sai maãu vaø ñoä leäch maãu
1) Ñònh nghóa:
Ta xeùt ñaùm ñoâng vôùi tæ leä caùc phaàn töû coù tính chaát A laø p.
Daáu hieäu X maø ta quan taâm laø caùc phaàn töû cuûa ñaùm ñoâng coù tính
chaát A hay khoâng: Neáu coù, ta ñaët X = 1; neáu khoâng, ta ñaët X = 0.
Nhö vaäy, ñaùm ñoâng X coù phaân phoái Bernoulli X ∼ B(p) nhö sau:
X 0 1
P q p
(q = 1-p).
Khi ñoù moät maãu côõ n laø moät boä goàm n ñaïi löôïng ngaãu nhieân
(X1, X2, …, Xn) maø moãi Xi ñeàu coù cuøng phaân phoái Bernoulli vôùi X:
Xi ∼ B(p), nghóa laø
Xi 0 1
P q p
Noùi caùch khaùc, moãi Xi chæ nhaän hai giaù trò: 0 (vôùi xaùc suaát q) vaø 1
(vôùi xaùc suaát p).
Tæ leä maãu cuûa ñaùm ñoâng X öùng vôùi maãu (X1, X2,…, Xn), kí
hieäu Fn, laø ñaïi löôïng ngaãu nhieân ñònh bôûi:
k
nii
i1
1
FXn
n
=
=∑
4
2) YÙ nghóa:
Khi ∞→n tæ leä maãu Fn hoäi tuï veà tæ leä ñaùm ñoâng p.
Do ñoù khi n khaù lôùn ta xaáp xæ:
p ≈ Fn
3) Chuù yù:
Döôùi Daïng 2 cuûa baûng, vieäc tính giaù trò cuûa tæ leä maãu raát
ñôn giaûn vì ta chæ caàn xaùc ñònh soá phaàn töû m thoûa tính chaát A
cuûa maãu côõ n. Khi ñoù
n
m
Fn= .
Ví duï: Ñeå khaûo saùt chæ tieâu X cuûa moät loaïi saûn phaåm, ngöôøi
ta quan saùt moät maãu vaø coù keát quaû sau:
X(cm) 11-15 15-19 19-23 23-27 27-31 31-35 35-39
Soá saûn phaåm 8 9 20 16 16 13 18
Nhöõng saûn phaåm coù chæ tieâu X töø 19 cm trôû xuoáng ñöôïc xeáp
vaøo loaïi B. Haõy xaùc ñònh kyø voïng maãu, phöông sai maãu, phöông
sai maãu hieäu chænh, ñoä leänh maãu, ñoä leänh maãu hieäu chænh cuûa chæ
tieâu X vaø tæ leä maãu caùc saûn phaåm loaïi B.
Giaûi.
Tröôùc heát ta thay caùc khoaûng xi- xi+1 baèng giaù trò trung
bình cuûa hai ñaàu muùt 2
'1+
+
=ii
i
xx
x.
Xi 13 17 21 25 29 33 37
ni 8 9 20 16 16 13 18
Ta coù:
- Côõ maãu n = 100.
- Kyø voïng maãu cuûa X laø
∑== ).(36,26
1cmnX
n
Xii
- Phöông sai maãu cuûa X laø:
222 22
ii
1
SXnX(7,4452)(cm).
n
=−=
∑
5
- Ñoä leäch maãu cuûa X laø:
S 7,4452 (cm)=
- Phöông sai maãu hieäu chænh cuûa X laø:
2
222
n
S S (7,4827) (cm ).
n1
==
−
- Ñoä leäch maãu hieäu chænh cuûa X laø: S 7,4827(cm)
=
- Tæ leä maãu caùc saûn phaåm loaïi B laø:
%.1717,0
100
17 ==== n
m
Fn
vì trong n = 100 saûn phaåm coù m = 8 + 9 = 17 saûn phaåm coù chæ
tieâu X nhoû hôn hay baèng 19 cm, nghóa laø coù m = 17 saûn phaåm loaïi
B.
Chuù yù: Ta coù theå söû duïng phaàn meàm thoáng keâ trong caùc maùy
tính boû tuùi CASIO 500MS, 570MS,..) nhö sau:
1) Vaøo MODE SD: Baám MODE… vaø baám soá öùng vôùi SD.
2) Xoùa boä nhôù thoáng keâ: Baám SHIFT MODE 1 (maøn hình
hieän leân Stat clear) = AC. Kieåm tra laïi: Baám REPLAY Up hoaëc
Down thaáy n = vaø ôû goùc soá 0 laø ñaõ xoùa.
3) Nhaäp soá lieäu:
13 ; 8 M+
17 ; 9 M+
21 ; 20 M+
25 ; 16 M+
29 ; 16 M+
33 ; 13 M+
37 ; 18 M+
Löu yù: Ñeå ñöôïc ; ta baám SHIFT ,
4) Kieåm tra vaø söûa soá lieäu sai:
Baám REPLAY Down ñeå kieåm tra soá lieäu. Thaáy soá lieäu
naøo sai thì ñeå maøn hình ngay soá lieäu ñoù, nhaäp soá lieäu ñuùng vaø
baám = thì soá lieäu môùi seõ thay cho soá lieäu cuõ.
Ví duï: Nhaäp sai 13 ; 18 M+. Khi kieåm tra ta thaáy:
- x1 = 13 (ñuùng).
- Freq1 = 18 (sai)
Söûa nhö sau: Ñeå maøn hình ôû Freq1 = 18, baám 8 vaø = thì
nhaän ñöôïc soá lieäu ñuùng Freq1 = 8.