BomonKTDT-§HGTVT
11
Ch−¬ng 2:
§¹i Sè Boolean
I. Kh¸i niÖm chung
1. Më ®Çu
Kü thuËt ®iÖn tö ngµy nay ®−îc chia lµm 2 nh¸nh lín kü thuËt ®iÖn tö t−¬ng tù
vµ kü thuËt ®iÖn tö sè. Kü thuËt ®iÖn tö sè ngµy cµng thÓ hiÖn nhiÒu tÝnh n¨ng −u
viÖt vÒ tèc ®é xö lý, kÝch th−íc nhá gän, kh¶ n¨ng chèng nhiÔu cao, tiªu thô ®iÖn
n¨ng Ýt …. Do ®ã, ®iÖn tö sè ®−îc øng dông réng r·i trong nhiÒu lÜnh vùc vµ ngµy
cµng trë thµnh mét phÇn thiÕt yÕu h¬n trong c¸c hÖ thèng vµ thiÕt bÞ ë hÇu hÕt c¸c
lÜnh vùc cã øng dông khoa häc kü thuËt vµ c«ng nghÖ míi (c¬ khÝ, ho¸ häc, y häc...).
H¬n n÷a, víi sù ph¸t triÓn cña m¹ch tÝch hîp ®· t¹o nªn sù thóc ®Èy cµng
m¹nh mÏ trong viÖc t¹o ra nh÷ng m¹ch sè cã ®é phøc t¹p cµng t¨ng. NÒn c«ng nghÖ
ban ®Çu chØ t¹o ®−îc c¸c m¹ch tÝch hîp cì nhá (S.S.I) nh−ng, ngµy nay, viÖc sö
dông c¸c m¹ch tÝch hîp cì võa (M.S.I), cì lín (L.S.I) vµ cùc lín (VLSI) ngµy cµng
trë nªn phæ biÕn.
Trong m¹ch sè, tÝn hiÖu ®Çu vµo ë 1 trong 2 tr¹ng th¸i logic 0 hoÆc 1 vµ ®Çu ra
còng ë 1 trong 2 tr¹ng th¸i 0 hoÆc 1tuú theo tÝn hiÖu ®Çu vµo vµ c¸c phÇn tö trong
m¹ch gäi lµ c¸c cæng logic. §Ó m« t¶ m¹ch sè ng−êi ta sö dông c«ng cô to¸n häc lµ
®¹i sè Boolean (®¹i sè logic). §©y lµ c¬ së to¸n häc cho mäi lÜnh vùc cã liªn quan
®Õn kü thuËt sè.
2. Mét sè kh¸i niÖm c¬ b¶n
+ §¹i sè logic: lµ mét tËp hîp S cña c¸c ®èi t−îng A, B, C … trong ®ã x¸c ®Þnh 2
phÐp to¸n céng logic vµ nh©n logic víi c¸c tÝnh chÊt sau:
TÝnh chÊt Tªn gäi
S chøa (A + B) vµ (A.B) tÝnh ®ãng kÝn
A + B = B + A
A.B = B.A
LuËt giao ho¸n
(A + B).C = A.C + B.C
A + B.C = (A + B).(A + C)
LuËt ph©n phèi
(A + B) + C = A + (B + C)
(A.B).C = A.(B.C)
LuËt kÕt hîp
A + A = A
A.A = A
A + B = B ⇔ A.B = A tÝnh nhÊt qu¸n
PTH-DTT
12
A + 0 = A
A . 0 = 0
A + 1 = 1
A . 1 = A
0.
1
=
=+
AA
AA
A. (A + B) ≡ A + A.B ≡ A LuËt hÊp thô
B
A
B
A
BABA
+=
=+
.
. LuËt De Morgan
CBCACBCABA
BAABA
BABAA
.....
.
+=++
+=+
+=+
10
01
=
=
≡AA
+ Gi¶n ®å Venn: ®©y lµ c¸ch biÓu diÔn trùc quan c¸c phÐp to¸n trong ®¹i sè logic.
Trªn gi¶n ®å Venn tËp hîp S ®−îc biÓu diÔn b»ng 1 « vu«ng cßn c¸c phÇn tö A, B,
C … ®−îc biÓu diÔn b»ng c¸c miÒn n»m trong « vu«ng ®ã. MiÒn kh«ng cã trªn gi¶n
®å ®−îc coi b»ng 0 vµ miÒn lín nhÊt (toµn bé « vu«ng) ®−îc coi b»ng ®¬n vÞ 1.
vÝ dô: tËp hîp S lµ mét nhãm c¸c sinh viªn vµ ®−îc biÓu diÔn bëi toµn bé miÒn trong
h×nh vu«ng; trong nhãm sinh viªn ®ã cã 2 nhãm phô A vµ B, víi sinh viªn thuéc
nhãm A cã tãc n©u trong khi c¸c sinh viªn cña nhãm B cã m¾t xanh.
Khi ®ã, phÇn giao cña A vµ B bao gåm c¸c sinh viªn cã c¶ m¾t xanh vµ tãc n©u
(A.B). Hä lµ thµnh viªn cña c¶ nhãm A vµ nhãm B.
Nhãm c¸c sinh viªn mµ cã tãc n©u hoÆc m¾t xanh cã thÓ ®−îc biÓu diÔn: A+B (®−îc
xem nh− hîp cña c¸c nhãm)
A.B hay
B
A
∩
A+B hay
B
A∪
BomonKTDT-§HGTVT
13
II. BiÕn vµ hµm logic
1. Kh¸i niÖm vÒ biÕn vµ hµm logic
+ BiÕn logic lµ mét kh¸i niÖm dïng thay cho thuËt ng÷ mÖnh ®Ò tuú ý, mÖnh ®Ò nµy
cã thÓ ®óng hoÆc sai vµ kh«ng cã kh¶ n¨ng mét mÖnh ®Ò võa ®óng võa sai, nghÜa lµ
biÕn logic chØ nhËn mét trong hai gi¸ trÞ lµ ®óng hoÆc sai
VÝ dô, c©u: “H«m nay lµ thø N¨m vµ trêi ®ang m−a” cã thÓ ®−îc biÓu diÔn
nh− sau:
C = A.B.
víi A : h«m nay lµ thø N¨m.
B: trêi ®ang m−a.
C: toµn bé c©u.
Khi nµo th× toµn bé c©u lµ ®óng?
Cã thÓ thiÕt lËp mét b¶ng liÖt kª c¸c tr−êng hîp ®óng(True) hay sai(False)
cho A vµ B:
A B C
sai
sai
®óng
®óng
sai
®óng
sai
®óng
sai
sai
sai
®óng
NÕu “1” ®−îc sö dông ®Ó thay thÕ cho ph¸t biÓu ®óng vµ “0” cho ph¸t biÓu sai
th× b¶ng trªn cã thÓ ®−îc biÓu diÔn l¹i nh− sau:
A B C
0
0
1
1
0
1
0
1
0
0
0
1
Nh− vËy, toµn bé c©u lµ ®óng khi A vµ B ®Òu ®óng cßn c¸c tr−êng hîp kh¸c C
sai.
+ Mét mÖnh ®Ò phøc t¹p ®−îc t¹o thµnh tõ c¸c mÖnh ®Ò ®¬n gi¶n ban ®Çu, nã nhËn
mét trong 2 gi¸ trÞ lµ ®óng hoÆc sai. Khi ®ã, ký hiÖu lµ F(A, B, C … ) hay F(x1, x2,
x3 …), ng−êi ta gäi ®ã lµ hµm logic cña c¸c biÕn A, B, C … hay cña x1, x2, x3 …
+ Trong kü thuËt sè c¸c gi¸ trÞ ®óng vµ sai cña biÕn logic hay hµm logic ®−îc ký
hiÖu lµ 1 vµ 0 (®©y ®¬n thuÇn lµ ký hiÖu mµ kh«ng ph¶i lµ ch÷ sè cña hÖ hai). Thªm
n÷a viÖc thùc hiÖn c¸c gi¸ trÞ logic cßn phô thuéc vµo viÖc chän c¸c trÞ sè vËt lý ®Ó
biÓu diÔn.
VÝ dô: víi vi m¹ch thuéc hä TTL ng−êi ta ®−a ra 2 c¸ch ký hiÖu cho møc logic
PTH-DTT
14
. Møc logic d−¬ng:
Xi = 1 øng víi møc ®iÖn ¸p cao 5V
Xi = 0 øng víi møc ®iÖn ¸p thÊp 0V
. Møc logic ©m:
Xi = 1 øng víi møc ®iÖn ¸p thÊp 0V
Xi = 0 øng víi møc ®iÖn ¸p cao 5V
2. C¸c hµm logic s¬ cÊp
a. Hµm logic s¬ cÊp mét biÕn
A F(A)
Fi 0 1 BiÓu thøc Tªn gäi
F1 0 0 0 H»ng sè 0
F2 0 1 A LÆp l¹i A YES
F3 1 0
A
§¶o biÕn A NOT
F4 1 1 1 H»ng sè 1
b. Hµm logic hai biÕn
A 0 0 1 1
B 0 1 0 1
Ký hiÖu vµ biÓu thøc ®¹i sè
cña hµm Tªn gäi cña hµm
F0 0 0 0 0 F0 = 0 H»ng sè 0
F1 0 0 0 1 F1 = A.B Nh©n logic AND
F2 0 0 1 0 F2 = BA. CÊm B
F3 0 0 1 1 F3 = A LÆp l¹i A
YES / BUFFER
F4 0 1 0 0 F4 = AB. CÊm A
INHIBITION
F5 0 1 0 1 F5 = B LÆp l¹i B
YES / BUFFER
F6 0 1 1 0 F6 = BA. + AB. = BA
⊕
Kh¸c dÊu / céng module
2 XOR
F7 0 1 1 1 F7 = A + B Céng logic OR
F8 1 0 0 0 F8 = BABA +=↓ Hµm Pierce NOR
BomonKTDT-§HGTVT
15
F9 1 0 0 1 F9 = A ~ B = BABA .. + §ång dÊu
F10 1 0 1 0 F10 =
B
Bï cña B
NOT B
F11 1 0 1 1 F11 = BAAB +=→ KÐo theo A
IMPLICATION
F12 1 1 0 0 F12 = A Bï cña A
NOT B
F13 1 1 0 1 F13 = BABA +=→ KÐo theo B
IMPLICATION
F14 1 1 1 0 F14 = A/B = BA. Hµm Sheffer
NAND
F15 1 1 1 1 F15 = 1 H»ng sè 1
C¸c hµm logic s¬ cÊp
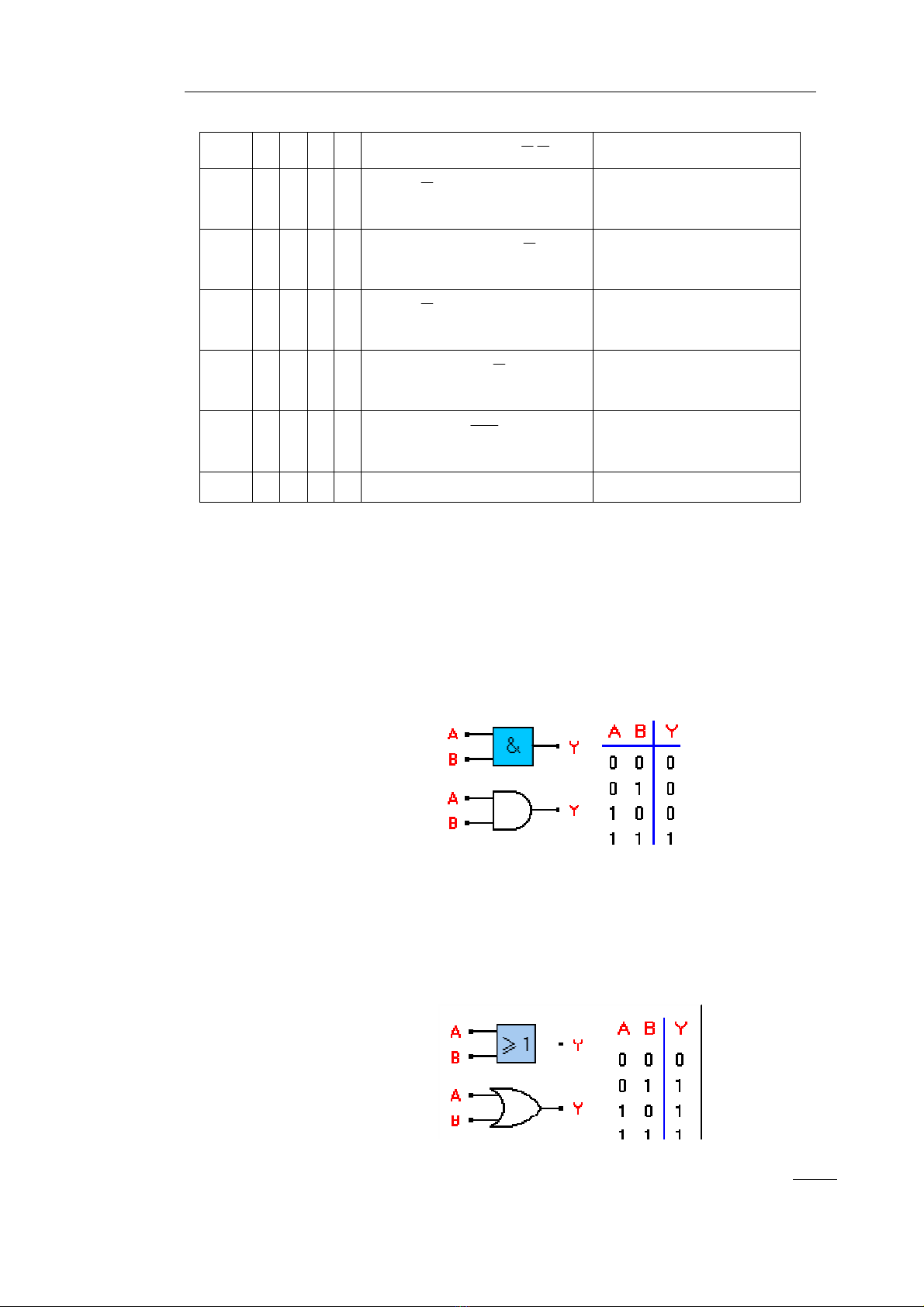
+ Hµm F(A,B) = A.B
Hµm nµy thùc hiÖn phÐp nh©n logic cña hai biÕn A vµ B. PhÇn tö thùc hiÖn
chøc n¨ng cña hµm trªn lµ phÇn tö AND (cßn gäi lµ cæng AND). Mét cæng AND cã
hai hay nhiÒu ®Çu vµo vµ chØ cã mét ®Çu ra. §Çu ra cã møc logic 1 chØ khi tÊt c¶ c¸c
®Çu vµo ë møc 1; vµ cã møc 0 khi mét trong c¸c ®Çu vµo ë møc 0. H×nh d−íi ®©y
chØ ra ký hiÖu vµ b¶ng ch©n lý cña cæng AND víi 2 ®Çu vµo.
Tæng qu¸t: Hµm AND chØ mang gÝa trÞ 1 khi c¸c ®Çu vµo ®ång thêi b»ng 1
+ Hµm F(A,B) = A + B
Hµm nµy thùc hiÖn phÐp céng logic. PhÇn tö thùc hiÖn lµ phÇn tö OR (cßn gäi
lµ cæng OR). Cæng OR cã møc logic cao khi cã Ýt nhÊt mét ®Çu vµo ë møc 1; vµ chØ
khi c¶ 2 ®Çu vµo ë møc logic 0 ®Çu ra cæng OR míi cã møc logic 0. Hµm OR cã ký
hiÖu vµ b¶ng ch©n lý nh− h×nh d−íi ®©y:
Tæng qu¸t: Hµm OR chØ mang gi¸ trÞ 0 khi tÊt c¶ c¸c ®Çu vµo ®ång thêi b»ng 0