ChươngIV:MchLogics
143
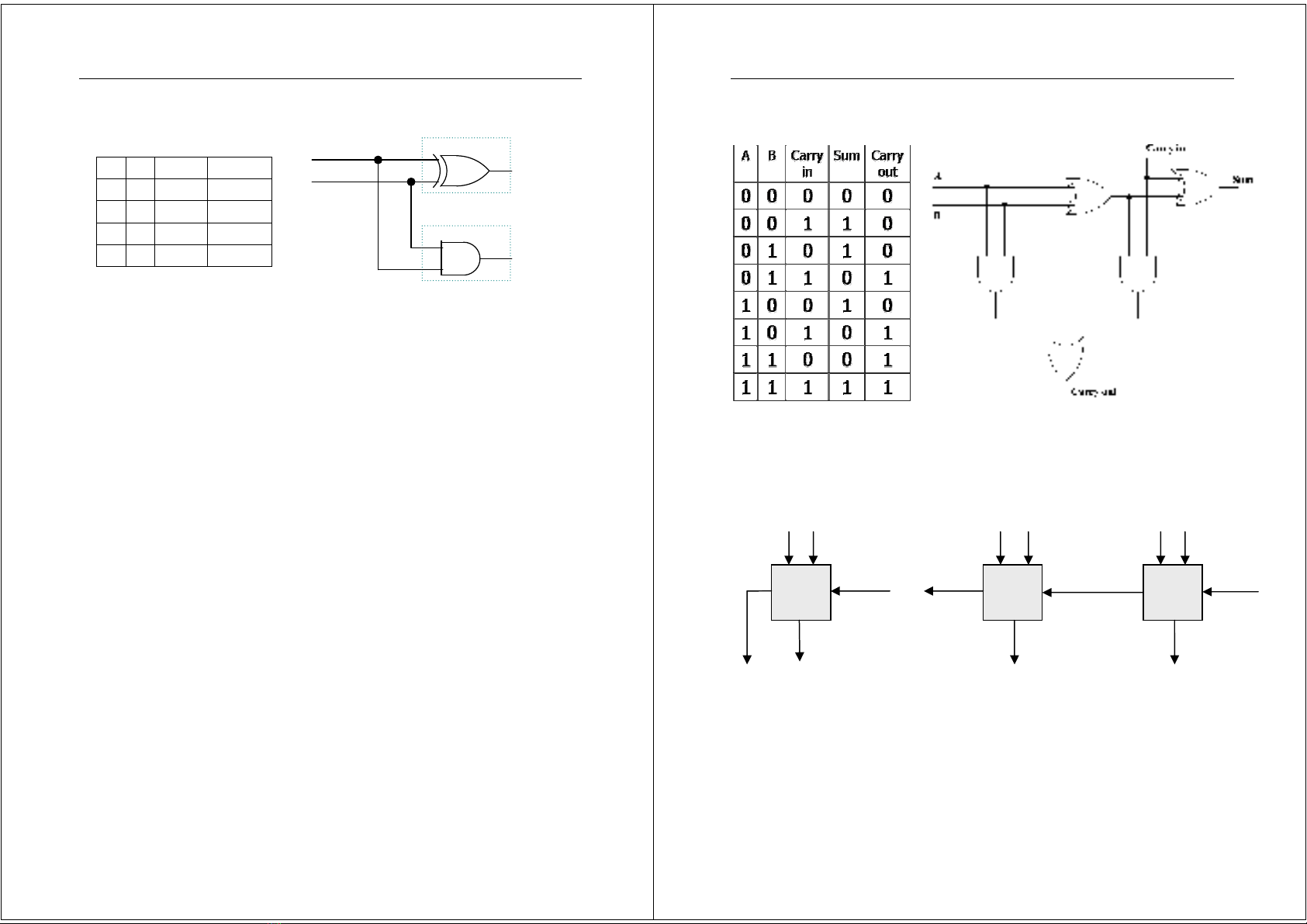
A
B
Sum
Carry
0 0 0 0
0 1 1 0
1 0 1 0
1 1 0 1

!"

#
Hình4.16.Bncacng
Bn^acngnàychchophéptatínhtngbitcGcph*ic+a
hait`ñVuvàonhiubit,nhưngkhôngthGchiDnñưZcchovtríbít
=gi<at`vìnókhôngxclýsmangt`bênph*isangvtrínày,
haynóicáchkháckhôngcngvQisnhQtrongphépcongthông
thưWng.Nhưv!ybncacngnàykhôngth ápdmngñ thi(tk(
mt b cngcho 2 s có nhiu bit, thayvào ñó, ph*i càn tQi b
cngñVyñ+(fulladderl).
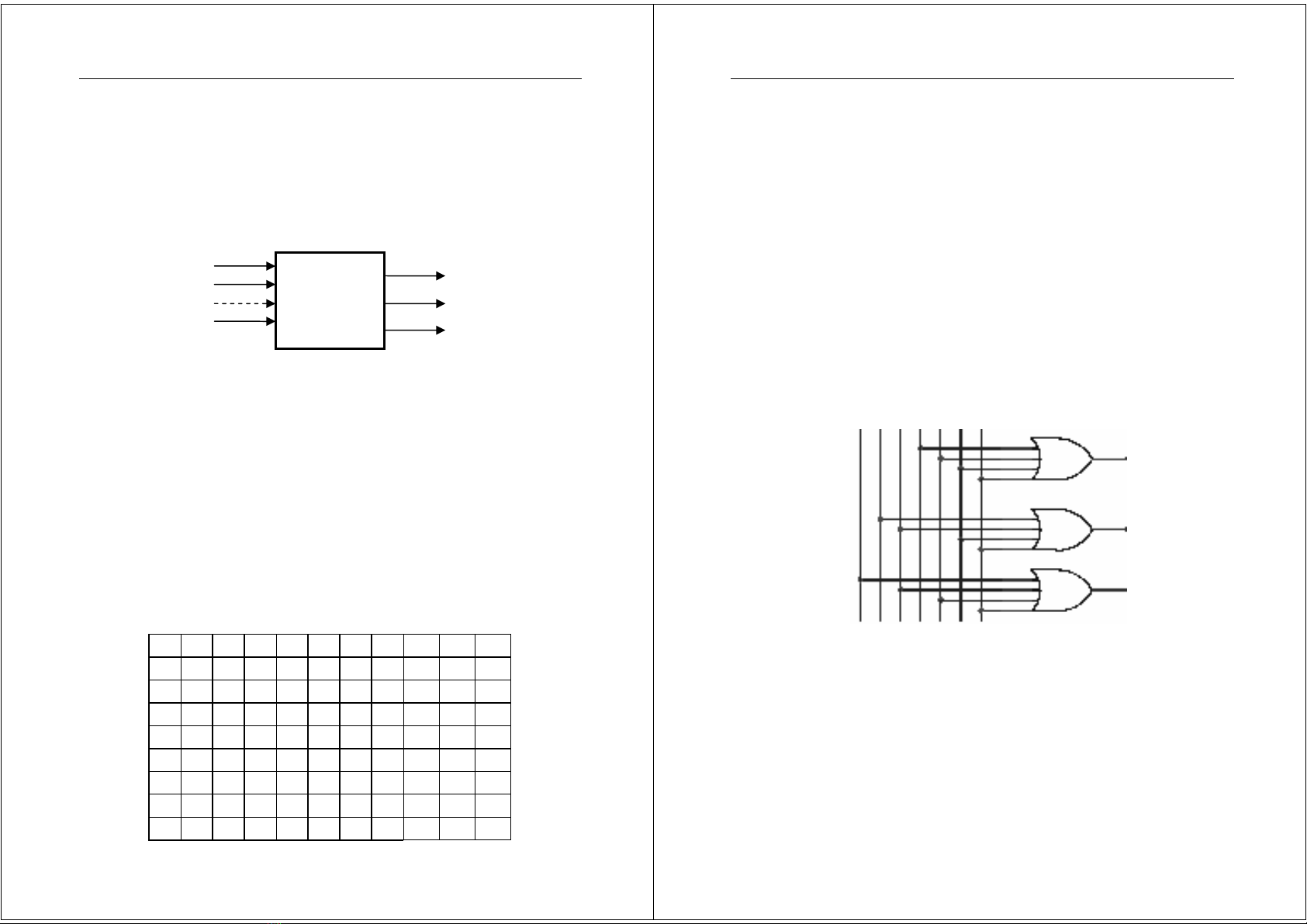
b)BJcJngñ;yñ?(FullAdder)
B*ngchântrvàm-chchobcng1bitñVyñ+tronghình
4.17.BcngñVyñ+ñưZccButhànht`haibncacng.ðVura
Sum
là1n(usliA,B,và
Carryin
b\ng1.
Carryout
b\ng1
khic*A và Bñub\ng 1(ñVuvào trái c+acngOR)hocñúng
mttrongschúngb\ng1vàbitCarryincũngb\ng1.
Gi*scñ(t-obcngchohait`AvàB,meit`16bt,ch
viDcsaochépm-chtronghình4.12ñúng16lVn.SnhQt`bítñưZc
dùnglàmsnhQvàobitbêntrái.SnhQvàobtcGctráiñưZcni
vào0.Lo-ibcngnàyñưZcg$ilàbcngsnhQ
ripple(ripple
carryadder)
.VìtrongtrưWnghZpxBunhBt,cng1vào111...11
1(nhphân),snhQripplet`bitcGcph*isangbitcGctráithìmQi
cngxongñưZc.DoñótrongcáctrưWnghZpnhưv!ythìbcng
nàys8rBtch!mvàkhônghiDuqu*.CũngcóbcngkhôngcósG
ChươngIV:MchLogics
144
trfnày,vàdoñónhanhhơn.SơñybcngñVyñ+chonbitnhư
hình4.18.
Hình4.17.BcngñVyñ+
4.3.5.M"chgi?imãvàmãhóa
Kháini[m:
M-chmãhoá
(ENCODER
)làm-chcónhiDmvmbi(nñi
nh<ngkýhiDuquenthucvQiconngưWisangnh<ngkýhiDukhông
quen thuc con ngưWi. M-ch gi*i mã (
DECODER
) là m-ch làm
Full
Adder
Full
Adder
Full
Adder
Carry
in0=0
Carry
in1
Carry
out0
Carry
out1
Carry
inno1
S0
S1
Sno1
B0
A0
B1
A1
Bno1
Ano1
Sn
Hinh4.18.Bcngnbit
ChươngIV:MchLogics
145
nhiDmvmngưZcl-im-chmãhóa,bi(nñinh<ngkýhiDukhông
quenthucvQiconngưWisangnh<ngkýhiDuquenthucvQicon
ngưWi.
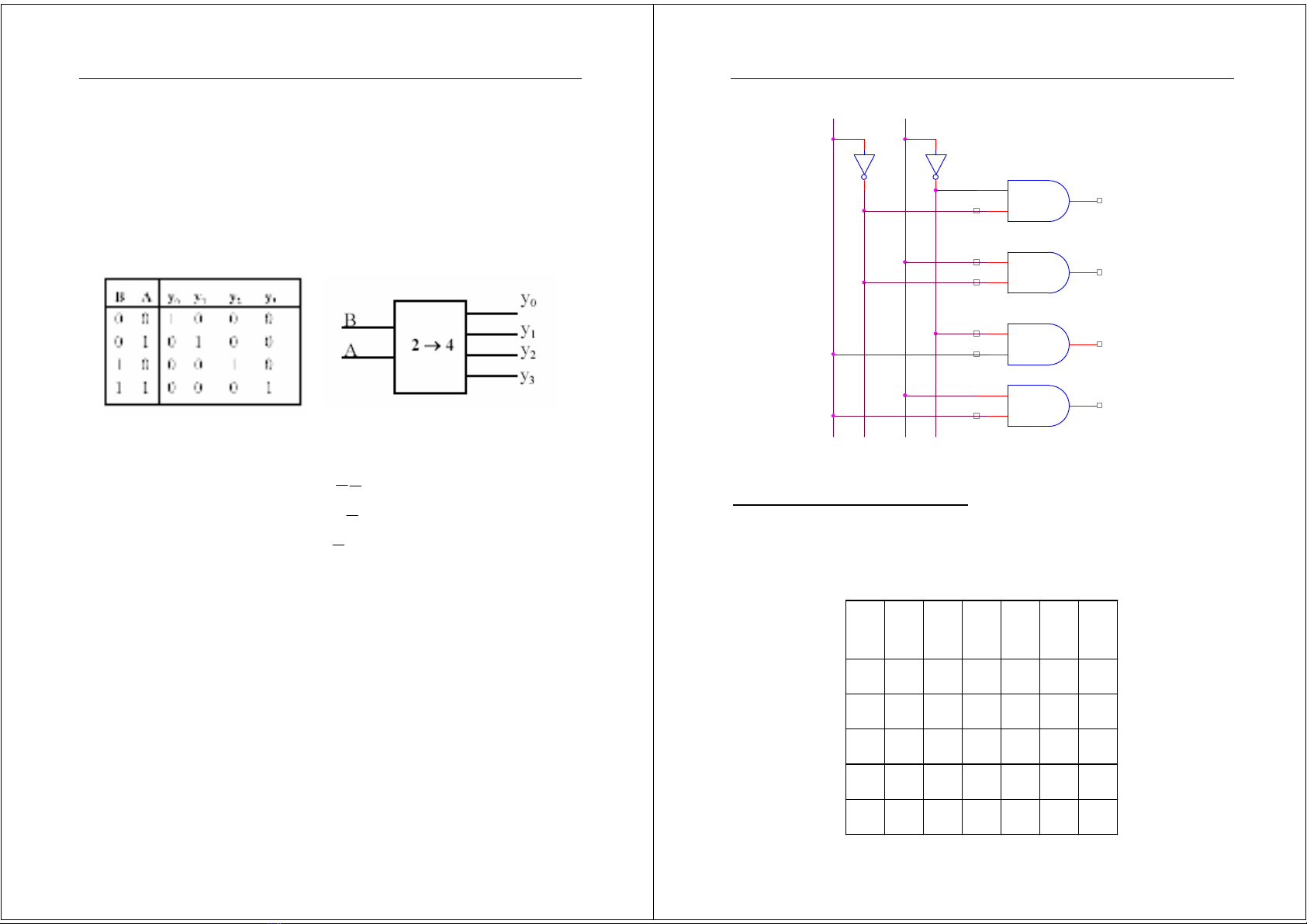
a)M"chmãhoá(Encoder)
Xétm-chmãhóanhphânt`8sang3(8ngõvàovà3ngõ
ra).Sơñykhic+am-chñưZcchotrênhình4.19.
Trongñó:
ox
0
,x
1
,…,x
7
làcácngõvàotínhiDu.
oA
0
,A
1
,A
2
làcácngõra.
M-chmãhóanhphân8
3thGchiDnbi(nñitínhiDungõ
vàothànhmtt`mãnhphântương^ng=ngõra,cmth nhưsau:
0
000 2
100 4
100 6
110
1
001 3
011 5
101 7
111
Ch$nm^ctácñng(tíchcGc)=ngõvàolàm^clogic1,ta
cób*ngtr-ngtháimôt*ho-tñngc+am-chnhưsau:
x
7
x
S
x
T
x
4
x
3
x
2
x
1
x
0
A
2
A
1
A
0
0 0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 1 0 0 0 1
0 0 0 0 0 1 0 0 0 1 0
0 0 0 0 1 0 0 0 0 1 1
0 0 0 1 0 0 0 0 1 0 0
0 0 1 0 0 0 0 0 1 0 1
0 1 0 0 0 0 0 0 1 1 0
1 0 0 0 0 0 0 0 1 1 1
ENCODER
8
3
x
0
x
1
x
7
A
0
A
1
A
2
Hình4.19.SơñykhiEncoder8
3
ChươngIV:MchLogics
146
Gi*ithíchb*ngtr-ngthái:Khimtngõvào=tr-ngtháicao
(m^clogic1)vàcácngõvàocònl-ithBp(m^clogic0)thìngõra
xuBthiDnt`mãtương^ng.Ngõvàonào=tr-ngtháicaothìtương
^ngvQiconsñó=hDth!pphân,vídmngõvào4=tr-ngtháicao
s8tương^ngvQis4ñưZcñưavàongõnh!p.Cmthlà:khingõ
vàox
0
=1vàcácngõvàocònl-ib\ng0thìt`mã=ngõralà000,
khingõvàox
1
=1vàcácngõvàocònl-ib\ng0thìt`mãnhphân
=ngõralà001,…
Phươngtrìnhlogictigi*n:
A
0
=x
1
+x
3
+x
5
+x
7
A
1
=x
2
+x
3
+x
6
+x
7
A
2
=x
4
+x
5
+x
6
+x
7
Sơ
ñym-chc+aENCODER8
3nhưhình4.20.

x
1
x
2
x
3
x
4
x
5
x
6
x
7
A
2

A
1
A
0
Hình4.20.ENCODER8
3
TươngtGtadfdàngcóth thi(tk(m-chmãhóath!pphân,
dùngmãhóacácst`0ñ(n9sanghDnhphân.TrongtrưWnghZp
nàytacVncó4ñVurañ mãhóañưZcs8(1000)và9(1001).
ChươngIV:MchLogics
147
b)M"chgi?imã(Decoder)
NgưZcvQim-chmãhóa,m-chgi*imãlàm-chthZpñi
thôngtinnhphânvQinngõnh!pthành2
n
ngõxuBt.N(ungõnh!p
cómtsthZpkhôngdùngthìsngõracóth íthơn2
n
.Khiñó
m-chgi*imãg$ilàm-chgi*imãnom,vQi
n
m2≤.
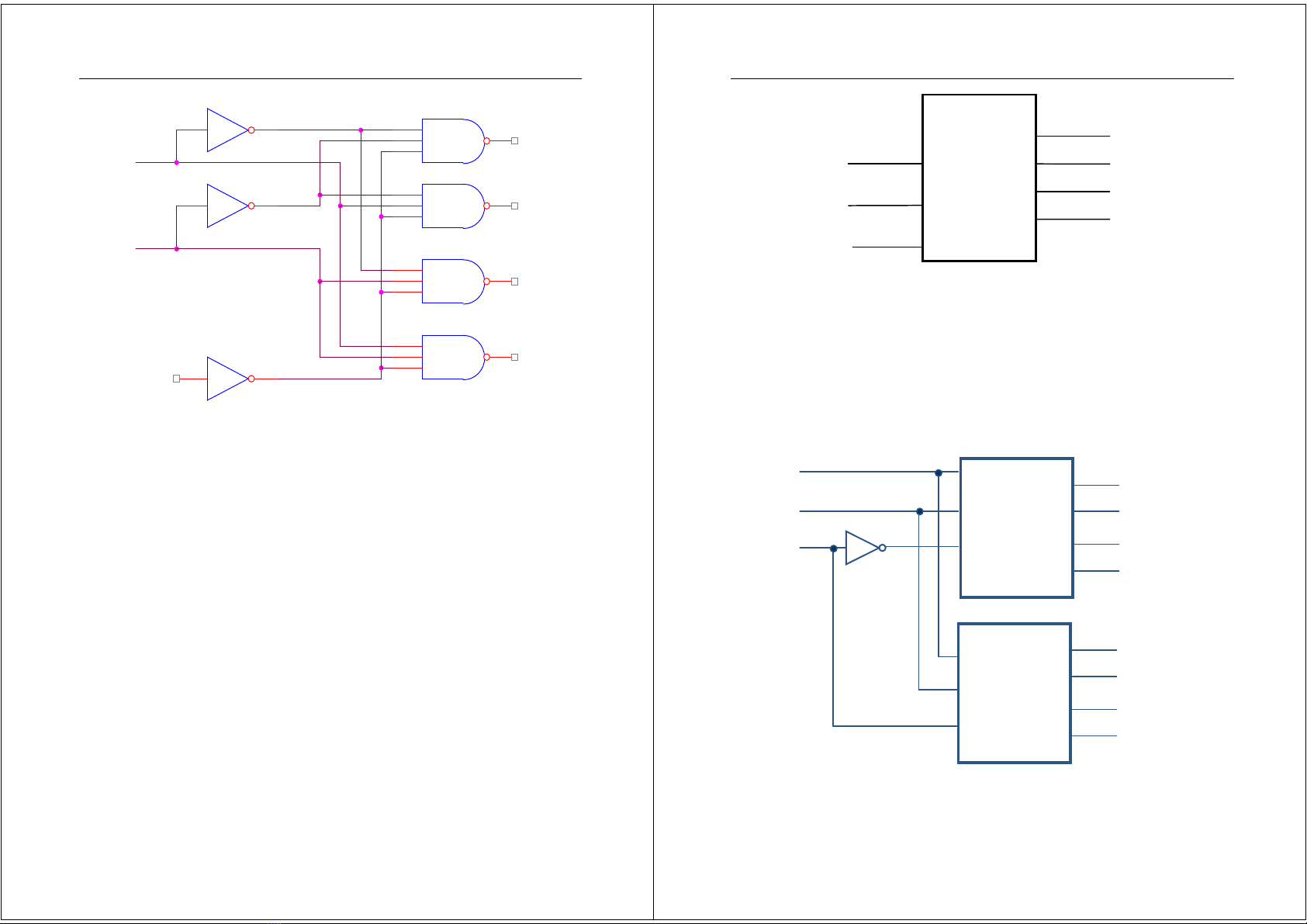
ð ñơngi*ntaxétm-chgi*imã2o4vQisơñykhivà
b*ngchântrm-chgi*imãnhphân2
4nhưhình4.21.
Hình4.21.Decoder2
4
T`b*ngchântrtacóphươngtrìnhlogictigi*nchom-ch:
ABy
BAy
BAy
BAy
=
=
=
=
3
2
1
0
Sơñym-chc+aDECODER2
4nhưhình4.22.
M-ch gi*i mã ñưZc ñóng gói thành các vi m-ch và ñưZc
bánratrênthtrưWngthưWngcód-ng4o16,3o8và2o4kép(t^chai
bgi*imãñưZcñóngchungvàotrongmtvim-chñơn).Ngoàira
còn phbi(n bgi*i mã 4o10 dùnggi*i mã s nh phân sang hD
th!pphân.Ngoàicácngõnh!pvàxuBtd<liDuthưWngcòncómt
ngõñiukhi nho-tñngc+am-ch.NgõnàythưWngkýhiDulàE,
khiE=1,chophépm-chho-tñngvàkhiE=0thìkhôngcho
phépm-chho-tñng.
ChươngIV:MchLogics
148








Hình4.22.Sơñym-chDecoder2
4
Mchgi&imãvVicngNAND
Mtsm-chgi*imãñưZct-ot`cngNANDthayvìcng
AND.Nót-orangõxuBttheod-ngñ*ol-i.Hình4.23làm-chgi*i
mã2
4vQicngNANDvQimtñưWngvàoñiukhi nE.Tương
^ngvQinólàB*ngchântrsau:
1
1
1
1
1
1
1
1
x
x
x
x
1
1
0
0
1
1
1
1
1
1
1
1
1
1
0
0
1
1
0
0
1
1
1
1
0
0
1
1
0
0
1
1
1
1
0
0
1
1
1
1
0
0
0
0
1
1
1
1
1
1
0
0
0
0
0
0
0
0
D3
D3
D2
D2
D1
D1
D0
D0
A0
A0
A1
A1
E
E
1
1
1
1
1
1
1
1
x
x
x
x
1
1
0
0
1
1
1
1
1
1
1
1
1
1
0
0
1
1
0
0
1
1
1
1
0
0
1
1
0
0
1
1
1
1
0
0
1
1
1
1
0
0
0
0
1
1
1
1
1
1
0
0
0
0
0
0
0
0
D3
D3
D2
D2
D1
D1
D0
D0
A0
A0
A1
A1
E
E
ChươngIV:MchLogics
149
Hình4.23.M-chgi*imãvQicngNAND
M-chnàyh$atñngkhitínhiDuñiukhi nE=0vàngõra
s8cógiátr0tương^ngvQisnhphân=cácngõvào.KhiE=1
thìkhôngchophépm-chho-tñngt^clàkhôngphmthucvàocác
giátrñVuvào,ñVuraluônb\ng1.
Cácm-chgi*imãngoàithtrưWngthưWngñưZcñónggói
vàcókýhiDunhưhình4.24.ðólà mtm-chgi*mã2
4dùng
cng AND và vQi mt ñưWng ñiu khi n E cho phép m-ch ho-t
ñngkhiE=1vàkhôngho-tñngkhiE=0.




















ChươngIV:MchLogics
150
Mr3ngm"chgi?imã
TrongmtstrưWnghZpcVnm-chgi*imãvQimtkínhcO
lQnmàtal-ichcóm-chvQikíchthưQcnh_hơnthìtacóth ghép
haihocnhiuhơncácm-chñangcóñt-omtm-chmãhóalQn
hơn.Vídmtacóth t-om-chgi*imã3
8t` haim-chgi*i mã
2
4 (hình 4.25). Trong trưWng hZp này ta ñã t!n dmng ngõ vào
ñiukhi nEñ làmngõnh!pth^3.
DECODER
2x4
2
0
2
1
E
D
0
D
1
D
2
D
3
Hình4.24.KýhiDuDecoder2
4







Hình4.25.M-chgi*imã3
8
ChươngIV:MchLogics
151
CÂUHZIVÀBÀIT\PCHƯƠNGIV
1.L!pb*ngchântrvàv8sơñym-chchohàm4bi(nsau:
a)x=AB+A(C+D)
b)y=(A+BC)(D+AB)
c)z=
)( DACBA ++

2.Rútg$ncáchàmsaudùngcácñnhlýc+aBooleanalgebra
a)x=
BCDAACD +
b)y=AB+A(
DCCD +
)
c)z= ))((
DCBADACB ++
3.DùngñnhlýDeMorgan,rútg$nbi uth^csauchoñ(nkhich
cònbi(nñơnñ*o(mtg-chtrên)
 z=
)).(( DBCA ++
4.Mtnhàlu!nlýh$cláixevàomttiDmbánñyăn,ngyitrongxe
ông nói: “Làm ơn cho tôi mt bánh Hambuger
hoZc
xúc xích
và
khoaitâychiên”.Ti(cr\ngngưWibánhàngcònchưah$ch(tlQp6
và không bi(t (và không mun bi(t) trong hai t` logic “hoc” và
“và”thìt`nàoñưZcưutiên.Anhtachor\ngtrongtrưWnghZpnày
difngi*ith(nàocũngñưZc.TrongtrưWnghZpnàodưQiñâylàdifn
ñ-tñúngñơnñthàng:
 a)ChHambuger
 b)Chxúcxích
 c)Chkhoaitâychiên
 d)Xúcxíchvàkhoaitâychiên
 e)Hambugervàkhoaitâychiên
 f)Xúcxíchvàhambuger
ChươngIV:MchLogics
152
 g)TBtc*3th^
 h)Khôngcógì–nhàlu!nlýbñóibmngvìquáthôngminh
5.Mtnhàtruyngiáol-cñưWngt-ingãr8ba=chngd`ngNam
California.Ôngtabi(thaitoánñixemáy=khuvGcnày,mttoán
luônnóith!tvàmttoánluônnóidi.Ôngtamunbi(tñưWngnào
ñitQiDisneylandthìôngtaph*iñtcâuh_inhưth(nào?
6.ð làmmtthi(tbñiukhi nbáoñngtrongxehơi,ngưWita
thi(tk(1m-chbáoñngnhưsau:
TínhiDu:
o
DRV(driver)=m^ccaokhitàix(ngyivàogh(láivà=
m^cthBpkhikhôngngyivào;
o
Bph!nñánhlca:1–b!t,0–tJt;
o
BELT=m^ccaokhitàix(càidâyantoànvà=m^c
thBpkhikhôngcàidâyantoàn.
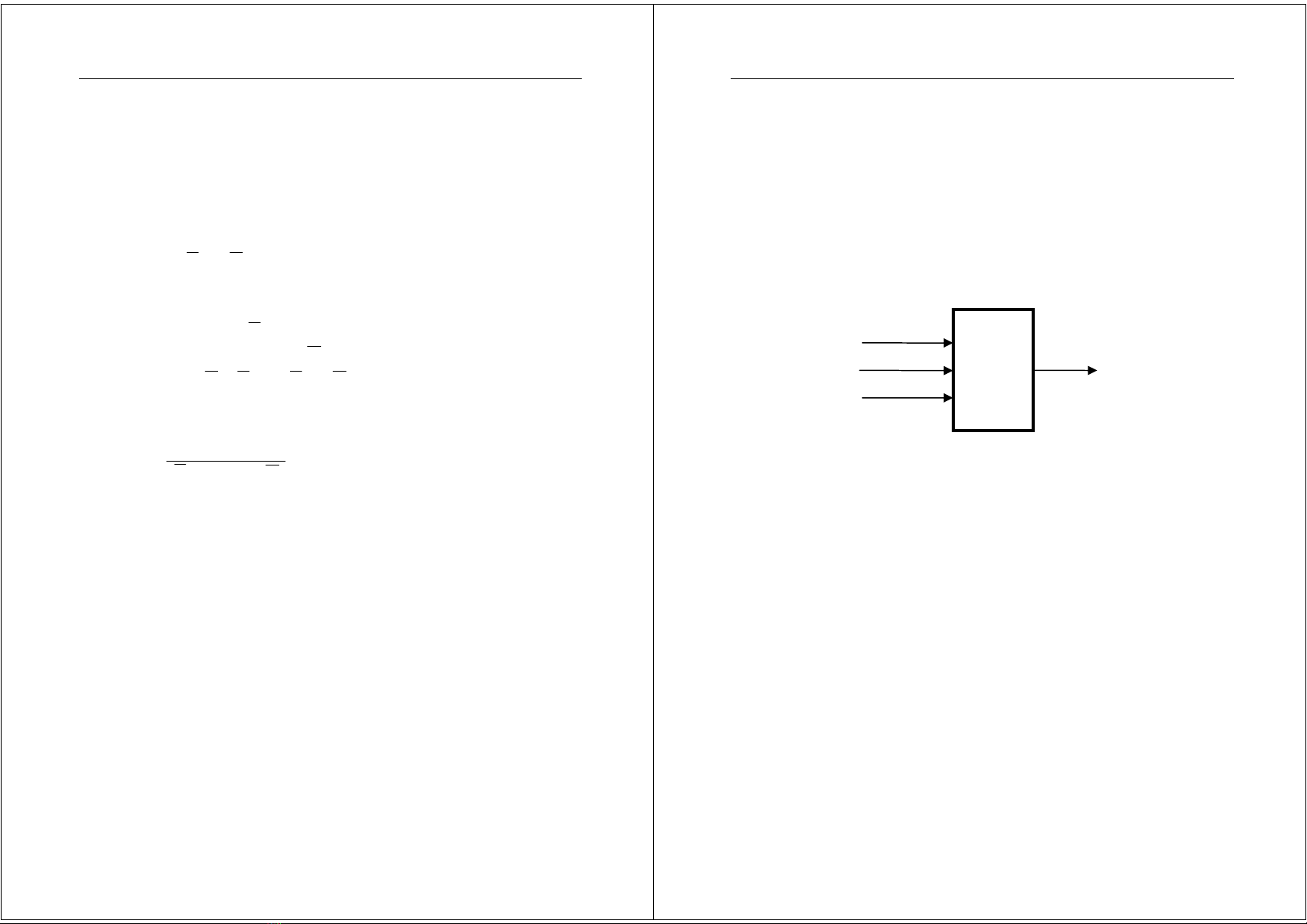
Hãythi(tk(m-chlogicvQi3ñVuvào(DRV,bph!nñánh
lca,BELT),1ñVura(báoñng),saochobph!nbáoñngs8ho-t
ñng(báoñng=1)khitynt-imttrong2tr-ngtháisau:
o
Tàix(chưangyivàoxetronglúcbph!nñánhlcab!t,
o
Tàix(ñãngyivàoxenhưngchưacàidâyantoàntrong
lúcbph!nñánhlcab!t
L!pb*ngchântrc+ahàmra.
7.ðơngi*ncáchàmsaudùngb*nñyKarnaugh
a)
∑
=
)6,4,3,2,0(),,(
CBAf
b)
∑
=
)15,11,7,5,4,2,1,0(),,,(
DCBAf
Mch
Logic
DRV
Bph!nñánhlca
BELT
Báoñng