bé gi¸o dôc vµ ®µo t¹o Kú thi tuyÓn sinh ®¹i häc, cao §¼nG n¨m 2002
------------------------------ M«n thi : to¸n
§Ò chÝnh thøc (Thêi gian lµm bµi: 180 phót)
_____________________________________________
C©u I (§H : 2,5 ®iÓm; C§ : 3,0 ®iÓm)
Cho hµm sè : (1) ( lµ tham sè).
23223 )1(33 mmxmmxxy −+−++−= m
1. Kh¶o s¸t sù biÕn thiªn vµ vÏ ®å thÞ hµm sè (1) khi .1
=
m
2. T×m k ®Ó ph−¬ng tr×nh: − cã ba nghiÖm ph©n biÖt. 033 2323 =−++ kkxx
3. ViÕt ph−¬ng tr×nh ®−êng th¼ng ®i qua hai ®iÓm cùc trÞ cña ®å thÞ hµm sè (1).
C©u II.(§H : 1,5 ®iÓm; C§: 2,0 ®iÓm)
Cho ph−¬ng tr×nh : 0121loglog 2
3
2
3=−−++ mxx (2) ( lµ tham sè). m
1 Gi¶i ph−¬ng tr×nh (2) khi .2
=
m
2. T×m ®Ó ph−¬ng tr×nh (2) cã Ýt nhÊt mét nghiÖm thuéc ®o¹n [m3
3;1 ].
C©u III. (§H : 2,0 ®iÓm; C§ : 2,0 ®iÓm )
1. T×m nghiÖm thuéc kho¶ng )2;0(
π
cña ph−¬ng tr×nh: .32cos
2sin21
3sin3cos
sin +=
+
+
+x
x
xx
x
5
2. TÝnh diÖn tÝch h×nh ph¼ng giíi h¹n bëi c¸c ®−êng: .3,|34| 2+=+−= xyxxy
C©u IV.( §H : 2,0 ®iÓm; C§ : 3,0 ®iÓm)
1. Cho h×nh chãp tam gi¸c ®Òu ®Ønh cã ®é dµi c¹nh ®¸y b»ng a. Gäi ABCS.,S
M
vµ lÇn l−ît N
lµ c¸c trung ®iÓm cña c¸c c¹nh vµ TÝnh theo diÖn tÝch tam gi¸c , biÕt r»ng SB .SC aAMN
mÆt ph¼ng ( vu«ng gãc víi mÆt ph¼ng . )AMN )(SBC
2. Trong kh«ng gian víi hÖ to¹ ®é §ªcac vu«ng gãc Oxyz cho hai ®−êng th¼ng:
∆ vµ ∆.
=+−+
=−+−
0422
042
:
1zyx
zyx
+=
+=
+=
tz
ty
tx
21
2
1
:
2
a) ViÕt ph−¬ng tr×nh mÆt ph¼ng chøa ®−êng th¼ng )(P1
∆
vµ song song víi ®−êng th¼ng .
2
∆
b) Cho ®iÓm . T×m to¹ ®é ®iÓm )4;1;2(M
H
thuéc ®−êng th¼ng 2
∆
sao cho ®o¹n th¼ng
MH
cã ®é dµi nhá nhÊt.
C©u V.( §H : 2,0 ®iÓm)
1. Trong mÆt ph¼ng víi hÖ to¹ ®é §ªcac vu«ng gãc Oxy , xÐt tam gi¸c vu«ng t¹i , ABC A
ph−¬ng tr×nh ®−êng th¼ng lµ BC ,033 =−− yx c¸c ®Ønh vµ A
B
thuéc trôc hoµnh vµ
b¸n kÝnh ®−êng trßn néi tiÕp b»ng 2. T×m täa ®é träng t©m cña tam gi¸c . G ABC
2. Cho khai triÓn nhÞ thøc:
n
x
n
n
n
x
x
n
n
x
n
x
n
n
x
n
n
x
x
CCCC
+
++
+
=
+
−
−
−
−
−
−
−
−−
−
−
3
1
3
2
1
1
3
1
2
1
1
2
1
0
3
2
1
22222222 L
( n lµ sè nguyªn d−¬ng). BiÕt r»ng trong khai triÓn ®ã C vµ sè h¹ng thø t−
13 5nn C=
b»ng , t×m vµ n20 n
.
----------------------------------------HÕt---------------------------------------------
Ghi chó: 1) ThÝ sinh chØ thi cao ®¼ng kh«ng lµm C©u V.
2) C¸n bé coi thi kh«ng gi¶i thÝch g× thªm.
Hä vµ tªn thÝ sinh:.................................................... Sè b¸o danh:.....................
1
bé gi¸o dôc vµ ®µo t¹o Kú thi tuyÓn sinh ®¹i häc, cao ®¼ng n¨m 2002
------------------------------------- §¸p ¸n vµ thang ®iÓm
m«n to¸n khèi A
C©u ý Néi dung §H C§
I1
23 31 xxym +−=⇒=
TËp x¸c ®Þnh Rx ∈∀ . )2(363' 2−−=+−= xxxxy ,
=
=
⇔= 2
0
0'
2
1
x
x
y
10",066" =⇔==+−= xyxy
B¶ng biÕn thiªn
∞+∞− 210x
−
'
y +
0 −
0
−+ 0
"
y
y + ∞ lâm U 4
CT 2 C§
0 låi ∞−
=
=
⇔= 3
0
0x
x
y , 4)1( =−y
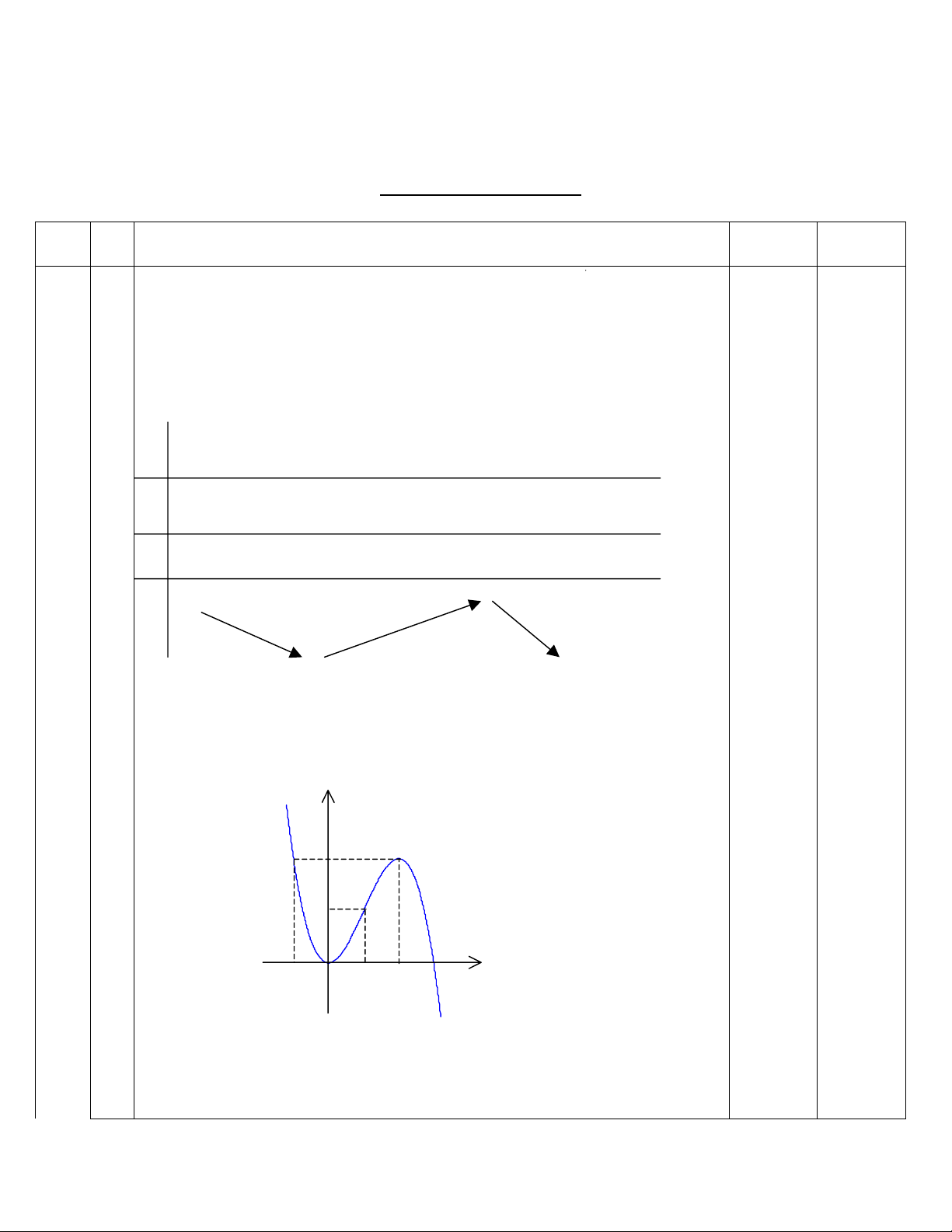
§å thÞ:
( ThÝ sinh cã thÓ lËp 2 b¶ng biÕn thiªn)
∑1,0 ®
0,25 ®
0,5 ®
0,25 ®
∑1,5 ®
0,5®
0,5 ®
0,5 ®
-11 2 3 x
0
2
4
y
2
I2
C¸ch I. Ta cã 2332323 33033 kkxxkkxx +−=+−⇔=−++− .
§Æt 23 3kka +−= Dùa vµo ®å thÞ ta thÊy ph−¬ng tr×nh axx =+− 23 3
cã 3 nghiÖm ph©n biÖt 43040 23 <+−<⇔<<⇔ kka
()( )
>−+
<≠
⇔
>+−+
<≠
⇔021
30
0)44)(1(
30
2
2kk
k
kkk
k
≠∧≠
<<−
⇔20
31
kk
k
C¸ch II. Ta cã
[
]
03)3()(033 222323 =−+−+−⇔=−++− kkxkxkxkkxx
cã 3 nghiÖm ph©n biÖt 03)3()( 22 =−+−+=⇔ kkxkxxf
cã 2 nghiÖm ph©n biÖt kh¸c k
≠∧≠
<<−
⇔
≠−+−+
>++−=∆
⇔20
31
033
0963
222
2
kk
k
kkkkk
kk
∑5,0 ®
0,25 ®
0,25 ®
-----------
0,25®
0,25 ®
∑5,0 ®
0,25 ®
0,25 ®
-----------
0,25 ®
0,25 ®
3
C¸ch I.
3)(3)1(363 222' +−−=−++−= mxmmxxy ,
+=
−=
⇔= 1
1
0
2
1
'
mx
mx
y
Ta thÊy 21 xx ≠ vµ 'y ®æi dÊu khi qua 1
x vµ ⇒
2
x hµm sè ®¹t cùc trÞ t¹i
1
x vµ 2
x.
23)( 2
11 −+−== mmxyy vµ 23)( 2
22 ++−== mmxyy
Ph−¬ng tr×nh ®−êng th¼ng ®i qua 2 ®iÓm cùc trÞ
(
)
23;1 2
1−+−− mmmM vµ
(
)
23;1 2
2++−+ mmmM lµ:
⇔
+−+
=
+−
4
23
2
12mmymx mmxy +−= 2
2
C¸ch II. 3)(3)1(363 222' +−−=−++−= mxmmxxy , Ta thÊy
0'09)1(99' 22 =⇒>=−+=∆ ymm cã 2 nghiÖm 21 xx ≠
vµ 'y ®æi dÊu khi qua 1
x vµ ⇒
2
x hµm sè ®¹t cùc trÞ t¹i 1
x vµ 2
x.
Ta cã 23223 )1(33 mmxmmxxy −+−++−=
()
.23363
33
1222 mmxmmxx
m
x+−+−++−
−=
Tõ ®©y ta cã mmxy +−= 2
11 2 vµ mmxy +−= 2
22 2.
VËy ph−¬ng tr×nh ®−êng th¼ng ®i qua 2 ®iÓm cùc trÞ lµ mmxy +−= 2
2.
∑1,0 ®
0,25 ®
0,25 ®
0,25 ®
0,25 ®
----------
0,25 ®
0,25 ®
0,25 ®
0,25 ®
∑1,0 ®
0,25 ®
0,25 ®
0,25 ®
0,25 ®
-----------
0,25 ®
0,25®
0,25 ®
0,25 ®
II 1.
Víi 2=m ta cã 051loglog 2
3
2
3=−++ xx
§iÒu kiÖn 0>x. §Æt 11log2
3≥+= xt ta cã
06051 22 =−+⇔=−+− tttt .
2
3
2
1
=
−=
⇔t
t
∑5,0 ®
0,25 ®
∑0,1 ®
0,5 ®
3
3
1−=
t (lo¹i) , 3
3
2
32 33log3log2 ±
=⇔±=⇔=⇔= xxxt
3
3±
=x tháa m·n ®iÒu kiÖn 0>x.
(ThÝ sinh cã thÓ gi¶i trùc tiÕp hoÆc ®Æt Èn phô kiÓu kh¸c)
0,25 ® 0,5 ®
2.
0121loglog 2
3
2
3=−−++ mxx (2)
§iÒu kiÖn 0>x. §Æt 11log2
3≥+= xt ta cã
0220121 22 =−−+⇔=−−+− mttmtt (3)
.21log13log0]3,1[ 2
33
3≤+=≤⇔≤≤⇔∈ xtxx
VËy (2) cã nghiÖm ]3,1[ 3
∈ khi vµ chØ khi (3) cã
nghiÖm
[]
2,1∈. §Æt tttf += 2
)(
C¸ch 1.
Hµm sè )(tf lµ hµm t¨ng trªn ®o¹n
][
2;1 . Ta cã 2)1( =f vµ 6)2( =f.
Ph−¬ng tr×nh 22)(22
2+=⇔+=+ mtfmtt cã nghiÖm
[]
2;1
∈
.20
622
222
22)2(
22)1( ≤≤⇔
≤+
+≤
⇔
+≥
+≤
⇔m
m
m
mf
mf
C¸ch 2.
TH1. Ph−¬ng tr×nh (3) cã 2 nghiÖm 21 ,tt tháa m·n 21 21 <≤< tt .
Do 1
2
1
2
21 <−=
+tt nªn kh«ng tån t¹i m.
TH2. Ph−¬ng tr×nh (3) cã 2 nghiÖm 21 ,tt tháa m·n
21 21 ≤≤≤ tt hoÆc 21 21 tt ≤≤≤
()
200242 ≤≤⇔≤−−⇔ mmm .
(ThÝ sinh cã thÓ dïng ®å thÞ, ®¹o hµm hoÆc ®Æt Èn phô kiÓu kh¸c )
∑0,1 ®
0,25 ®
0,25 ®
-----------
0,25 ®
0,25 ®
0,25 ®
0,25 ®
∑0,1 ®
0,25 ®
0,25 ®
----------
0,25 ®
0,25 ®
0,25 ®
0,25 ®
III 1.
532cos
2sin21
3sin3cos
sin +=
+
+
+x
x
xx
x. §iÒu kiÖn 2
1
2sin −≠x
Ta cã 5 =
+
+
+x
xx
x2sin21
3sin3cos
sin 5
+
+++
x
xxxxx
2sin21
3sin3cos2sinsin2sin
=5 =
+
++−+
x
xxxxx
2sin21
3sin3cos3coscossin 5x
x
xx cos5
2sin21
cos)12sin2( =
+
+
VËy ta cã: 02cos5cos232coscos5 2=+−⇔+= xxxx
2cos =x (lo¹i) hoÆc ).(2
32
1
cos Zkkxx ∈+±=⇒=
π
π
∑1,0 ®
0,25 ®
0,25 ®
0,25 ®
∑1,0 ®
0,25 ®
0,25 ®
0,25 ®
4
2.
V×
(
0∈x;
)
π
2 nªn lÊy 3
1
π
=x vµ 3
5
2
π
=x . Ta thÊy 21 ,xx tháa m·n ®iÒu
kiÖn 2
1
2sin −≠x. VËy c¸c nghiÖm cÇn t×m lµ: 3
1
π
=x vµ 3
5
2
π
=x.
(ThÝ sinh cã thÓ sö dông c¸c phÐp biÕn ®æi kh¸c)
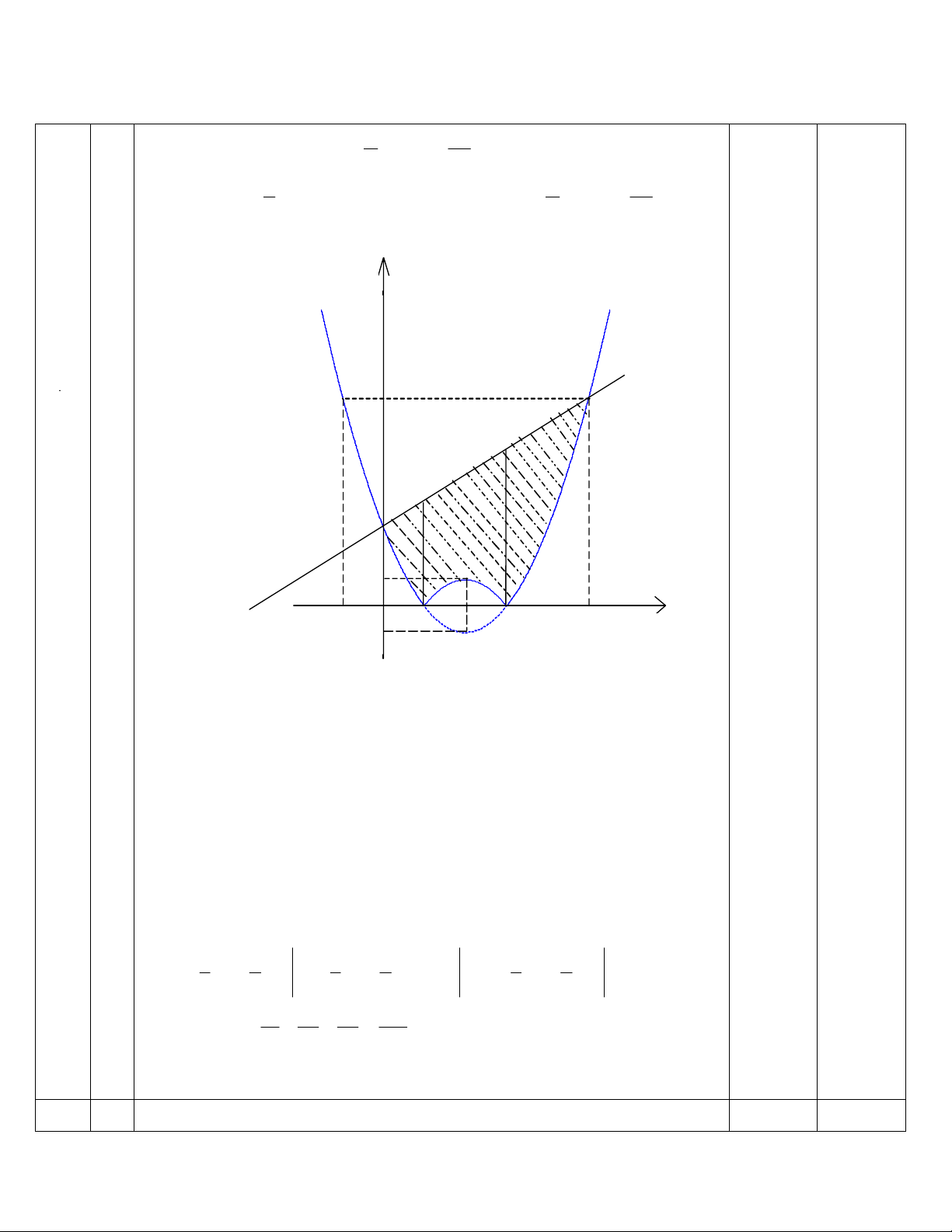
Ta thÊy ph−¬ng tr×nh 3|34| 2+=+− xxx cã 2 nghiÖm 0
1=x vµ .5
2=x
MÆt kh¸c ∀+≤+− 3|34| 2xxx
[]
5;0
∈
x. VËy
()()()
dxxxxdxxxxdxxxxS ∫∫∫+−+++−+−+=+−−+=
1
0
3
1
22
5
0
2343343|34|3
()
dxxxx
∫−+−++
5
3
2343
()( )()
dxxxdxxxdxxxS ∫∫∫ +−++−++−=
5
3
2
3
1
2
1
0
25635
5
3
23
3
1
23
1
0
23
2
5
3
1
6
2
3
3
1
2
5
3
1
+−+
+−+
+−= xxxxxxxS
6
109
3
22
3
26
6
13 =++=S (®.v.d.t)
(NÕu thÝ sinh vÏ h×nh th× kh«ng nhÊt thiÕt ph¶i nªu bÊt ®¼ng thøc
∀+≤+− 3|34| 2xxx
[]
5;0∈x)
0,25 ®
∑1,0 ®
0,25 ®
0,25 ®
0,25 ®
0,25®
0,25 ®
∑1,0 ®
0,25 ®
0,25 ®
0,25 ®
0,25®
IV 1. ∑1®∑1®
x
5
1
0
-1
y
3
3
2
1
8
-1