Tr ng THPT Tân Qu iườ ớ www.VNMATH.com
CHUYÊN Đ Ề
PH NG PHÁP T A Đ TRONG M T PH NGƯƠ Ọ Ộ Ặ Ẳ
A. LÝ THUY TẾ
I. T a đọ ộ
1. H tr c to đ ệ ụ ạ ộ Oxy g m ba tr c ồ ụ Ox, Oy đôi m t vuông góc v i nhau v i ba vect đ n v ộ ớ ớ ơ ơ ị
,i j
r ur
( )
1i j
= =
r r
.
2.
( )
1 2 1 2
;
a
a a a a i a j
=
⇔ +
uur ur ur uur
; M(x;y)⇔
OM xi y j
= +
uuuuur ur uur
3. T a đ c a vect :ọ ộ ủ ơ cho
( ; ), ( '; ')u x y v x y
r r
a.
'; 'u v x x y y= ⇔ = =
r r
b.
( )
'; 'u v x x y y± = ± ±
r r
c.
d.
. ' 'u v xx yy
= +
ur r
e.
' ' 0u v xx yy⊥ ⇔ + =
r r
f.
2 2
u x y
= +
r
g.
( )
cos ,
.
.
=
ur r
r r
r r
u v u v
u v
.
4. T a đ c a đi m:ọ ộ ủ ể cho A(xA;yA), B(xB;yB)
a.
( )
;
B A B A
AB x x y y= − −
uuur
b.
( ) ( )
2 2
B A B A
AB x x y y= − + −
c. G là tr ng tâm tam giác ọABC ta có:
xG=
; yG=
3
ABC
y y y+ +
d. M chia AB theo t s ỉ ố k:
;
1 1
A B A B
M M
x kx y ky
x y
k k
− −
= =
− −
Đ c bi t:ặ ệ M là trung đi m c a ể ủ AB:
; .
2 2
A B A B
M M
x x y y
xy
+ +
= =
II. Ph ng trình đ ng th ngươ ườ ẳ
1. M t đ ng th ng ộ ườ ẳ ∆ đ c xác đ nh khi bi t m t đi m ượ ị ế ộ ể M(x0;y0) và m t vect pháp tuy n ộ ơ ế
( )
;n A B=
r
ho c m t vect ch ph ng ặ ộ ơ ỉ ươ
( )
;a a b=
r
Ph ng trình t ng quát ươ ổ
( ) ( )
0 0 0 0A x x y y Ax By C− + − = ⇔ + + =
.
Ph ng trình tham s : ươ ố
,
( )
t R∈
.
Ph ng trình đ ng th ng qua ươ ườ ẳ M có h s góc ệ ố k:
( )
0 0
y k x x y= − +
.
2. Kho ng cách t m t đi m ả ừ ộ ể M(xM;yM) đ n m t đ ng th ng ế ộ ườ ẳ ∆:
0Ax By C+ + =
là:
( )
2 2
,M M
Ax By C
d M A B
+ +
∆ = +
.
III. Ph ng trình đ ng trònươ ườ
1. M t đ ng tròn đ c xác đ nh khi bi t tâm ộ ườ ượ ị ế I(a;b) và bán kính r.
Ph ng trình:ươ
D ng 1: ạ
( ) ( )
2 2 2
x a y b r− + − =
.
Chuyên đ : ềPH NG PHÁP T A Đ TRONG M T PH NGƯƠ Ọ Ộ Ặ Ẳ
1
a
n
∆
(C)
r
∆
I
M
GSP 4.06.exe
Tr ng THPT Tân Qu iườ ớ www.VNMATH.com
D ng 2: ạ
2 2 2 2 0x y ax by d+ − − + =
, đi u ki n ề ệ
2 2 0a b d+ − >
và
2 2
r a b d= + −
.
2. Đi u ki n đ đ ng th ng ề ệ ể ườ ẳ ∆:
0Ax By C+ + =
ti p xúc v i đ ng tròn (ế ớ ườ C) là:
( )
2 2
,Aa Ba C
d I r
A B
+ +
∆ = =
+
IV. Ba đ ng conicườ
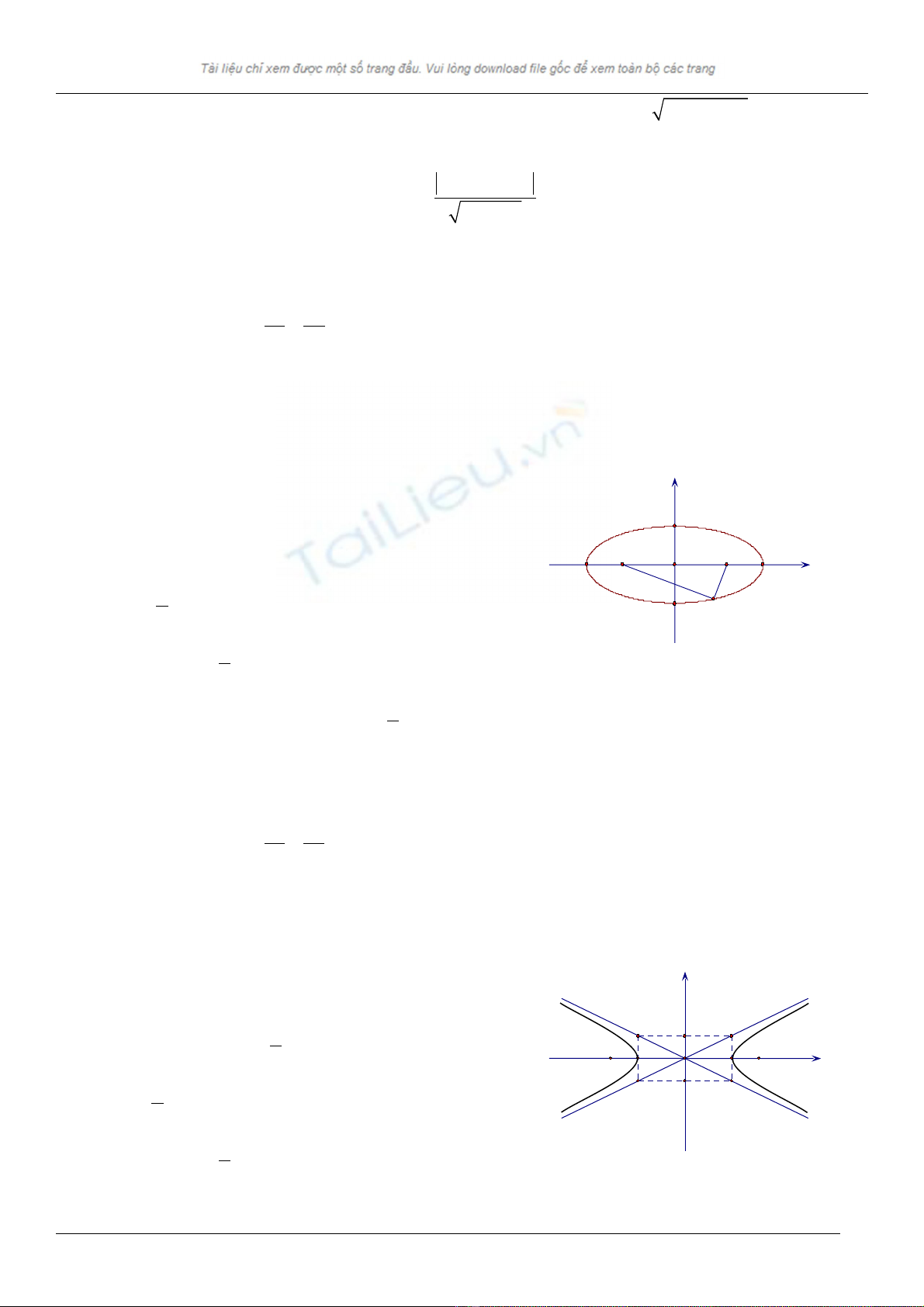
Elip
1. Ph ng trình chính t c: ươ ắ
2 2
2 2 1
x y
a b
+ =
, (a>b>0).
2. Các y u t : ế ố
2 2 2
c a b= −
, c>0.
Tiêu c : ựF1F2=2c; Đ dài tr c l n ộ ụ ớ A1A2=2aĐ dài tr c bé ộ ụ B1B2=2b.
Hai tiêu đi m ể
( ) ( )
1 2
;0 , ;0F c F c−
.
B n đ nh: đ nh trên tr c l n ố ỉ ỉ ụ ớ
( ) ( )
1 2
;0 , ;0A a A a−
,
đ nh trên tr c bé ỉ ụ
( ) ( )
1 2
0; , 0;B b B b−
.
Bán kính qua tiêu đi m: ể
1 1 2 2
;
M M
MF r a ex MF r a ex= = + = = −
Tâm sai:
1
c
ea
= <
Đ ng chu n: ườ ẩ
a
xe
= ±
Kho ng cách gi a hai đ ng chu n: ả ữ ườ ẩ
2a
de
=
.
3. Đi u ki n đ đ ng th ng ề ệ ể ườ ẳ Ax+By+C=0 ti p xúc v i elip là: ế ớ A2a2+B2b2=C2.
Hyperbol
1. Ph ng trình chính t c: ươ ắ
2 2
2 2 1
x y
a b
− =
, (a>0, b>0).
2. Các y u t : ế ố
2 2 2
c a b= +
, c>0.
Tiêu c : ựF1F2=2c; Đ dài tr c th c ộ ụ ự A1A2=2aĐ dài tr c o ộ ụ ả B1B2=2b.
Hai tiêu đi m ể
( ) ( )
1 2
;0 , ;0F c F c−
.
Hai đ nh: đ nh trên tr c th c ỉ ỉ ụ ự
( ) ( )
1 2
;0 , ;0A a A a−
,
Hai đ ng ti m c n: ườ ệ ậ
b
y x
a
= ±
Tâm sai:
1
c
ea
= >
Đ ng chu n: ườ ẩ
a
xe
= ±
Chuyên đ : ềPH NG PHÁP T A Đ TRONG M T PH NGƯƠ Ọ Ộ Ặ Ẳ
2
x
y
F2
F1
B2
B1
A2
A1
O
M
y=
b
ax
y=-
b
ax
B1
B2
A2
F2
A1
F1
O
y
x
Tr ng THPT Tân Qu iườ ớ www.VNMATH.com
Kho ng cách gi a hai đ ng chu n: ả ữ ườ ẩ
2a
de
=
3. Đi u ki n đ đ ng th ng ề ệ ể ườ ẳ Ax+By+C=0 ti p xúc v i hypebol là: ế ớ A2a2−B2b2=C2.
Parabol
1. Ph ng trình chính t c: ươ ắ
22y px=
, (p>0 g i là tham s tiêu).ọ ố
2. Các y u t :ế ố
M t tiêu đi m ộ ể
;0
2
p
F
÷
, đ ng chu n ườ ẩ
2
p
x= −
B. BÀI T P C B NẬ Ơ Ả
1. Trong m t ph ng ặ ẳ Oxy, tìm ph ng trình đ ng tròn có tâm ươ ườ I(1;0) và ti p xúc v i đ ng th ng (ế ớ ườ ẳ D)
3x–4y + 12 = 0.
2. Trong m t ph ng ặ ẳ Oxy cho Parabol (P) nh n ậOx làm tr c đ i x ng, đi qua g c t a đ và đi qua đi mụ ố ứ ố ọ ộ ể
( )
22;2 −M
.
a. L p ph ng trình c a (ậ ươ ủ P).
b. Đ ng th ng (ườ ẳ D) đi qua đi m ểE(2;0), song song v i đ ng th ng: ớ ườ ẳ
012 =−+− yx
và c t (ắP)
t i hai đi m ạ ể
21 ,FF
. Xác đ nh t a đ c a ị ọ ộ ủ
21 ,FF
.
c. Tính di n tích c a tam giác có m t đ nh n m trên đ ng chu n c a (ệ ủ ộ ỉ ằ ườ ẩ ủ P), còn hai đ nh kia là haiỉ
đ u dây đi qua tiêu đi m và song song v i tr c ầ ể ớ ụ Oy.
d. Tính di n tích hình ph ng gi i h n b i Parabol (ệ ẳ ớ ạ ở P) v i đ ng th ng (ớ ườ ẳ D).
3. Trong m t ph ng cho Elip: ặ ẳ
.144169 22 =+ yx
a. Tìm các tiêu đi m, tiêu c và tâm sai c a Elip.ể ự ủ
b. L p ph ng trình c a Parabol có đ nh trùng v i g c t a đ và có tiêu đi m trùng v i tiêuậ ươ ủ ỉ ớ ố ọ ộ ể ớ
đi m bên ph i c a Elip đã cho.ể ả ủ
4. Trong m t ph ng ặ ẳ Oxy cho Hyberbol (H) :
.1
45
22 =− yx
a. Tìm tâm sai và các ti m c n c a (ệ ậ ủ H).
b. L p ph ng trình ti p tuy n c a (ậ ươ ế ế ủ H) đi qua đi m ể
( )
4;5 −M
.
5. Trong mpOxy cho cho Parabol (P) có phu ng trình : ơ
xy 8
2=
.
a. Tìm t a đ c a tiêu đi m và ph ng trình đ ng chu n c a (ọ ộ ủ ể ươ ườ ẩ ủ P).
b. Ch ng minh r ng v i m i ứ ằ ớ ọ
0≠k
đ ng th ng : ườ ẳ
02 =−− kykx
luôn luôn c t (ắP) t i hai đi mạ ể
phân bi t.ệ
6. Trong mpOxy cho ba đi m ể
( ) ( )
.0;2,1;1),1;0( CBA −
a. Tìm tâm đ ng tròn ng ai ti p tam giác ườ ọ ế ABC và vi t ph ng trình đ ng tròn đó.ế ươ ườ
b. Vi t ph ng trình đ ng th ng đi qua ế ươ ườ ẳ A và vuông góc v i đ ng phân giác c a góc ph n tớ ườ ủ ầ ư
th ứI.
7. Trong m t ph ng ặ ẳ Oxy cho đi m ểF(3;0) và đ ng th ng (ườ ẳ D) có ph ng trình 3ươ x–4y+16=0.
a. Tính kho ng cách t đi m ả ừ ể F t i (ớD). Suy ra ph ng trình đ ng tròn có tâm là ươ ườ F và ti p xúcế
v i (ớD).
b. Vi t ph ng trình c a parabol (ế ươ ủ P) có tiêu đi m là ểF và có đ nh là g c t a đ ỉ ố ọ ộ O.
c. Ch ng t r ng (ứ ỏ ằ P) ti p xúc v i (ế ớ D), tìm t a đ ti p đi m. ọ ộ ế ể
8. Trong m t ph ng ặ ẳ Oxy cho Elip :
225259 22 =+ yx
.
a. Vi t ph ng trình chính t c và xác đ nh các tiêu đi m, tâm sai c a Elip.ế ươ ắ ị ể ủ
Chuyên đ : ềPH NG PHÁP T A Đ TRONG M T PH NGƯƠ Ọ Ộ Ặ Ẳ
3
B2
F2
y
x
O
Tr ng THPT Tân Qu iườ ớ www.VNMATH.com
b. M t đ ng tròn (ộ ườ C) có tâm I(0;1) và đi qua đi m ểA(4;2). Vi t ph ng trình c a đ ng tròn vàế ươ ủ ườ
ch ng t r ng (ứ ỏ ằ C) đi qua hai tiêu đi m c a Elip.ể ủ
9. Trong m t ph ng ặ ẳ Oxy cho Elip (E):
123 22 =+ yx
.
a. Tính đ dài tr c l n, tr c nh , t a đ hai tiêu đi m và tâm sai c a Elip (ộ ụ ớ ụ ỏ ọ ộ ể ủ E).
b. Cho đ ng th ng (ườ ẳ D) có ph ng trình: ươ
093 =+− ymx
. Tính m đ (ểD) ti p xúc v i (ế ớ E).
c. Vi t ph ng trình c a Parabol có đ nh trùng v i g c t a đ và có tiêu đi m là tiêu đi m bênế ươ ủ ỉ ớ ố ọ ộ ể ể
trái c a Elip đã cho.ủ
10. Trong mpOxy cho đ ng th ng (ườ ẳ D) có ph ng trình : ươ
0234 =+− yx
và F(2;0)
a. Vi t ph ng trình Parabol (ế ươ P) nh n ậF làm tiêu đi m và đ nh là g c t a đ .ể ỉ ố ọ ộ
b. Tìm kh ang cách t ỏ ừ F đ n đ ng th ng (ế ườ ẳ D). Tìm t a đ ti p đi m.ọ ộ ế ể
11. Trong mpOxy cho Elip (E) có ph ng trình : ươ
0225259 22 =−+ yx
.
a. Tìm t a đ tiêu đi m và tâm sai c a (ọ ộ ể ủ E).
b. Vi t ph ng trình đ ng th ng (ế ươ ườ ẳ D1) qua F1 và có h s góc ệ ố k = 1 và (D2) qua F2 và có h sệ ố
góc k= −1. Ch ng t (ứ ỏ D1)
⊥
(D2).
c. Vi t ph ng trình đ ng tròn tâm ế ươ ườ F2 qua giao đi m c a hai đ ng th ng (ể ủ ườ ẳ D1) và (D2). T đóừ
suy ra (D1) ti p xúc v i đ ng tròn.ế ớ ườ
12. Trong mpOxy cho F(0;3) và đ ng th ng (ườ ẳ D) :
01643 =+− yx
.
a. L p ph ng trình đ ng tròn tâm ậ ươ ườ F và ti p xúc v i (ế ớ D).
b. L p ph ng trình c a Parabol (ậ ươ ủ P) có tiêu đi m ểF và có đ nh là g c t a đ . Ch ng t r ng (ỉ ố ọ ộ ứ ỏ ằ P)
ti p xúc v i (ế ớ D). Tìm t a đ ti p đi m.ọ ộ ế ể
13. Trên m t ph ng t a đ ặ ẳ ọ ộ Oxy cho đ ng Hypebol v i ph ng trình : ườ ớ ươ
3x2 – y2 = 12.
a. Tìm t a đ các đ nh, tiêu đi m, tâm sai và ph ng trình các đ ng ti m c n c a hypebol đó.ọ ộ ỉ ể ươ ườ ệ ậ ủ
b. Tìm các giá tr c a tham s k đ đ ng th ng ị ủ ố ể ườ ẳ y = kx c t hypebol nói trên. ắ
14. Trên m t ph ng t a đ ặ ẳ ọ ộ Oxy cho ba đi m ểA(−1;2), B(2;1) và C(2;5).
a. Vi t ph ng trình tham s c a các đ ng th ng ế ươ ố ủ ườ ẳ AB và AC. Tính đ dài các đo n th ng ộ ạ ẳ AB và
AC.
b. Vi t ph ng trình đ ng tròn ngo i ti p ế ươ ườ ạ ế ∆ABC.
15. Trên m t ph ng ặ ẳ Oxy cho Elip có ph ng trình : ươ x2 + 4y2 = 4.
a. Tìm t a đ các đ nh, tiêu đi m và tâm sai c a elip.ọ ộ ỉ ể ủ
b. Đ ng th ng qua 1 tiêu đi m c a elíp và song song v i tr c ườ ẳ ể ủ ớ ụ Oy c t elíp t i 2 đi m ắ ạ ể M và N.
Tính đ dài đo n th ng ộ ạ ẳ MN.
c. Tìm giá tr c a k đ đ ng th ng ị ủ ể ườ ẳ y = x + k c t elíp đã cho.ắ
16. Trong m t ph ng ặ ẳ Oxy cho hypebol :
.1
94
22 =− yx
a. Xác đ nh t a đ các đ nh, t a đ các tiêu đi m, tâm sai và các ti m c n c a hypebol. Vị ọ ộ ỉ ọ ộ ể ệ ậ ủ ẽ
hypebol đã cho.
b. Tìm các giá tr c a n đ đ ng th ng ị ủ ể ườ ẳ y = nx – 1 có đi m chung v i hypebol.ể ớ
17. Trong m t ph ng ặ ẳ Oxy cho elíp (E) có ph ng trình 3ươ x2 + 5y2 = 30.
a. Xác đ nh t a đ các đ nh, t a đ các tiêu đi m và tâm sai c a elíp.ị ọ ộ ỉ ọ ộ ể ủ
b. M t đ ng th ng ộ ườ ẳ ∆ đi qua tiêu đi m ểF2(2;0) c a elíp (ủE), song song v i tr c tung, c t elíp (ớ ụ ắ E)
t i 2 đi m ạ ể A và B. Tính kho ng các t ả ừ A và B t i tiêu đi m ớ ể F1.
18. Trong m t ph ng ặ ẳ Oxy cho hai đi m ểA(2;3) và B(−2;1).
a. Vi t ph ng trình đ ng tròn đi qua hai đi m ế ươ ườ ể A, B và có tâm n m trên tr c hoành.ằ ụ
b. Vi t ph ng trình chính t c c a Parabol có đ nh là g c t a đ , đi qua đi m ế ươ ắ ủ ỉ ố ọ ộ ể A và nh n tr cậ ụ
hoành làm tr c đ i x ng. V đ ng tròn và Parabol tìm đ c trên cùng m t h tr c t a đ .ụ ố ứ ẽ ườ ượ ộ ệ ụ ọ ộ
19. Trong m t ph ng ặ ẳ Oxy cho hai đi m ểA(5;0) và B(4;3
)2
.
a. L p ph ng trình đ ng tròn nh n ậ ươ ườ ậ AB làm đ ng kính. Tìm t a đ các giao đi m c a đ ngườ ọ ộ ể ủ ườ
tròn và tr c hoành.ụ
Chuyên đ : ềPH NG PHÁP T A Đ TRONG M T PH NGƯƠ Ọ Ộ Ặ Ẳ
4
Tr ng THPT Tân Qu iườ ớ www.VNMATH.com
b. L p ph ng trình chính t c c a đ ng Elíp đi qua ậ ươ ắ ủ ườ A và B.
20. Trong m t ph ng v i h t a đ ặ ẳ ớ ệ ọ ộ Oxy, cho hypebol có ph ng trình :ươ
3694 22 =− yx
.
a. Xác đ nh t a đ các đ nh, t a đ các tiêu đi m và tâm sai c a hypebol.ị ọ ộ ỉ ọ ộ ể ủ
b. Vi t ph ng trình chính t c c a elíp đi qua đi m ế ươ ắ ủ ể
3;
2
37
M
và có chung các tiêu đi m v iể ớ
hypebol đã cho.
21. Trên m t ph ng t a đ ặ ẳ ọ ộ Oxy cho cho đ ng tròn (ườ C) có ph ng trình:ươ
.026
22 =−−+ yxyx
a. Xác đ nh t a đ tâm và bán kính c a đ ng tròn (ị ọ ộ ủ ườ C).
b. Ch ng minh r ng : Đ ng tròn (ứ ằ ườ C) đi qua g c t a đ ố ọ ộ O. G i ọOA là đ ng kính c a đ ngườ ủ ườ
tròn, vi t ph ng trình ti p tuy n c a đ ng tròn (ế ươ ế ế ủ ườ C) t i đi m ạ ể A.
22. Trong m t ph ng v i h tr c t a đ ặ ẳ ớ ệ ụ ọ ộ Oxy cho Elíp (E) :
.1
26
22 =+ yx
a. Xác đ nh t a đ các tiêu đi m và đ dài các tr c c a (ị ọ ộ ể ộ ụ ủ E).
b. Đi m M thu c (ể ộ E) nhìn hai tiêu đi m c a nó d i m t góc vuông. Vi t ph ng trình ti pể ủ ướ ộ ế ươ ế
tuy n c a (ế ủ E) t i ạM.
23. Trong m t ph ng t a đ ặ ẳ ọ ộ Oxy cho đ ng tròn (ườ C) có ph ng trình :ươ
0326
22 =−−−+ yxyx
.
a. Xác đ nh tâm và bán kính c a đ ng tròn (ị ủ ườ C).
b. Tìm các đi m thu c đ ng tròn (ể ộ ườ C) có hoành đ ộx = 1 và vi t ph ng trình ti p tuy n t i cácế ươ ế ế ạ
đi m đó.ể
24. Trong m t ph ng t a đ ặ ẳ ọ ộ Oxy, cho hypebol (H) đi qua đi m ể
4
9
;5M
và nh n đi m ậ ể
( )
0;5F
làm tiêu
đi m c a nó.ể ủ
a. Vi t ph ng trình chính t c c a hypebol (ế ươ ắ ủ H).
b. Vi t ph ng trình ti p tuy n c a (ế ươ ế ế ủ H) bi t r ng ti p tuy n đó song song v i đ ng th ngế ằ ế ế ớ ườ ẳ
0145 =−+ yx
.
25. Trong m t ph ng v i h tr c t a đ ặ ẳ ớ ệ ụ ọ ộ Oxy, cho m t elip (ộE) có kho ng cách gi a các đ ng chu n làả ữ ườ ẩ
36 và các bán kính qua tiêu đi m c a ể ủ M n m trên elip (ằE) là 9 và 15.
a. Vi t ph ng trình chính t c c a elip (ế ươ ắ ủ E).
b. vi t ph ng trình ti p tuy n c a elip (ế ươ ế ế ủ E) t i đi m ạ ể M.
26. Trong m t ph ng v i h t a đ ặ ẳ ớ ệ ọ ộ Oxy cho Elíp (E):
2 2
1
25 16
x y
+ =
có hai tiêu đi m là ể
1 2
,F F
.
a. Cho đi m ểM(3;m) thu c (ộE), hãy vi t ph ng trình ti p tuy n c a (ế ươ ế ế ủ E) t i ạM khi m>0.
b. Cho A và B là hai đi m thu c (ể ộ E) sao cho
1 2
8AF BF+ =
. Hãy tính
2 1
AF BF+
.
C. BÀI T P NÂNG CAOẬ
1. (CĐ Kh i B_2009ố) Trong m t ph ng v i h t a đ ặ ẳ ớ ệ ọ ộ Oxy, cho tam giác ABC có C(−1; −2), đ ng trungườ
tuy n k t ế ẻ ừ A và đ ng cao k t B l n l t có ph ng trình là 5ườ ẻ ừ ầ ượ ươ x+y−9=0 và x+3y−5=0. Tìm t a đọ ộ
các đ nh ỉA và B.
Chuyên đ : ềPH NG PHÁP T A Đ TRONG M T PH NGƯƠ Ọ Ộ Ặ Ẳ
5